Coordinate Geometry

Last Updated: August 23, 2024

Notes

Coordinate geometry, also known as analytic geometry, is the study of geometry using a coordinate system and is a key topic on the ACT Exam. This branch of mathematics merges algebra and geometry to solve problems involving shapes, sizes, and relative positions of figures on a plane. In coordinate geometry, points are represented using ordered pairs of numbers, and geometric figures are analyzed through equations.

Learning Objectives

For the ACT Math exam, you should focus on mastering key concepts in Coordinate Geometry, including understanding the Cartesian plane, plotting points, and interpreting graphs. Learn to find the distance between points, the midpoint of a segment, and the slope of a line. Study the equations of lines, including slope-intercept, point-slope, and standard forms. Additionally, practice solving problems involving the intersections of lines and curves, and understand the geometric transformations on the coordinate plane.

Cartesian Coordinate System

The Basics

The Cartesian coordinate system consists of two perpendicular number lines: the x-axis (horizontal) and the y-axis (vertical). These axes intersect at a point called the origin, denoted as (0,0). Each point in the plane can be described by an ordered pair of numbers (x, y).

x-coordinate (abscissa): The horizontal distance from the origin.
y-coordinate (ordinate): The vertical distance from the origin.

Quadrants

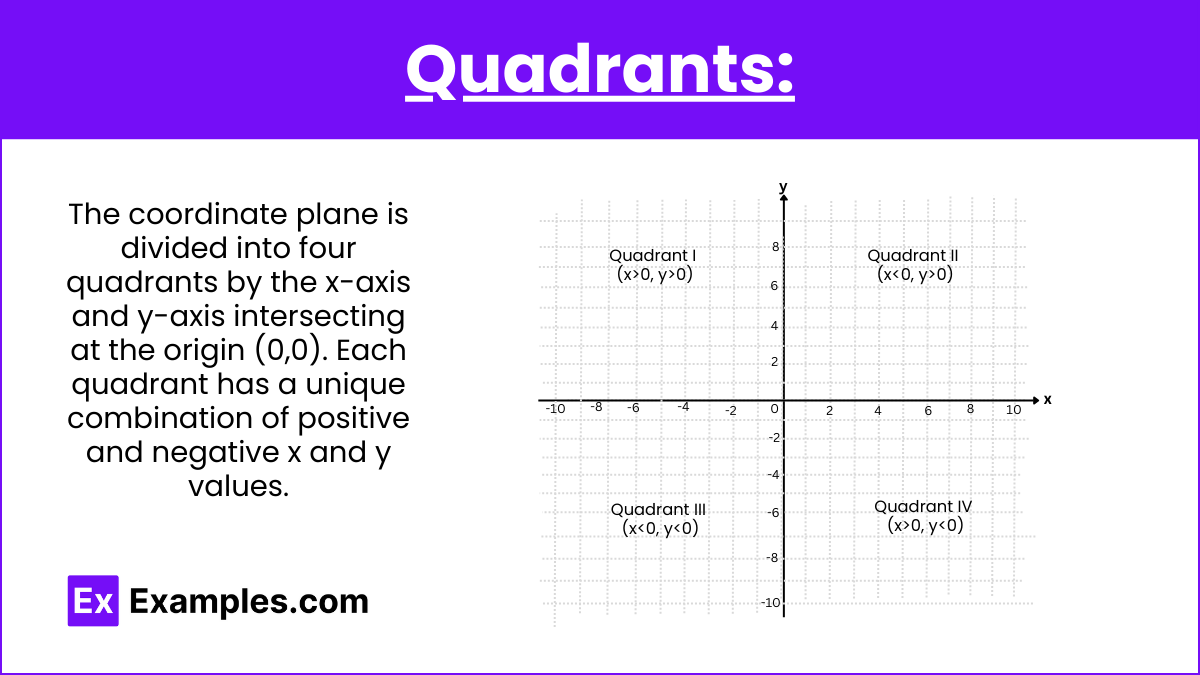
The coordinate plane is divided into four quadrants by the x-axis and y-axis intersecting at the origin (0,0). Each quadrant has a unique combination of positive and negative x and y values.

Quadrant I: In Quadrant I (x>0, y>0), both x and y coordinates are positive. It is located in the upper-right section of the plane.
Quadrant II: In Quadrant II In (x<0, y>0) has negative x and positive y coordinates. It is located in the upper-left section of the plane.
Quadrant III: In Quadrant III (x<0, y<0), both x and y coordinates are negative. It is situated in the lower-left section of the plane.
Quadrant IV: In Quadrant IV In (x>0, y<0) has positive x and negative y coordinates. It is found in the lower-right section of the plane.

Key Formulas in Coordinate Geometry

In coordinate geometry, several fundamental formulas are essential for solving problems related to distances, midpoints, and slopes of lines. Understanding and applying these formulas is crucial for analyzing geometric relationships on the coordinate plane. The key formulas include the distance formula, midpoint formula, and slope of a line.

Distance Formula

To find the distance between two points (x₁,y₁) and (x₂,y₂) in the coordinate plane, use the distance formula:

$d = \sqrt{(x₂-x₁)²+(y₂-y₁)²}$

Midpoint Formula

The midpoint of a segment connecting two points (x₁,y₁) and (x₂,y₂) is calculated using:

$M = \left(\frac{x₁+x₂}{2}, \frac{y₁+y₂}{2}\right)$

Slope of a Line

The slope (m) of a line measures its steepness and is calculated as:

$m = \frac{y₂-y₁}{x₂-x₁}$

Slope Types

The slope of a line describes its steepness and direction. Here are the different types of slopes:

Positive slope: The line rises from left to right, indicating an increase in y-values as x-values increase.
Negative slope: The line falls from left to right, indicating a decrease in y-values as x-values increase.
Zero slope: The line is horizontal, showing no change in y-values as x-values change.
Undefined slope: The line is vertical, indicating no change in x-values as y-values change, making the slope undefined.

Equation of a Line

Understanding the equation of a line is fundamental in algebra and geometry. There are three primary forms of linear equations: slope-intercept form, point-slope form, and standard form. Each form has its specific uses and advantages depending on the information available and the application required.

Slope-Intercept Form

The slope-intercept form of a line’s equation is: y=mx+b Here, m is the slope and b is the y-intercept. It’s useful for quickly graphing a line and understanding its slope and y-intercept.

Point-Slope Form

The point-slope form is useful when you know the slope and a point (x₁,y₁) on the line: y−y₁=m(x−x₁).

In this equation, m is the slope and (x₁,y₁) is a point on the line. This form is handy when you know a point on the line and its slope.

Standard Form

The standard form of a line’s equation is: Ax+By=C where A, B, and C are integers. This form is useful for finding intercepts and performing algebraic manipulations.

Parallel and Perpendicular Lines

Understanding the relationships between lines, specifically parallel and perpendicular lines, is fundamental in geometry and algebra. These relationships are primarily determined by the slopes of the lines.

Parallel Lines

Two lines are parallel if they have the same slope. For lines y=m₁x+b₁ and y=m₂x+b₂, they are parallel if m₁=m₂.

Perpendicular Lines

Two lines are perpendicular if the product of their slopes is −1. For lines y=m₁x+b₁ and y=m₂x+b₂, they are perpendicular if m1×m2=−1.

Circles in Coordinate Geometry

The study of circles in coordinate geometry involves understanding their equations and properties. The standard equation of a circle allows us to analyze and solve problems related to the position and size of circles in the coordinate plane. By knowing the center and the radius, we can describe the circle algebraically and graphically.