Plane Geometry

Last Updated: August 23, 2024

Notes

Plane geometry is the branch of mathematics that deals with shapes, sizes, and the properties of two-dimensional figures, and it is a key topic on the ACT Exam. It encompasses the study of points, lines, angles, triangles, quadrilaterals, and circles, among other shapes. Understanding these basic elements and their relationships is essential for solving geometry problems effectively and excelling in the ACT Math section.

Learning Objectives

For the ACT Math exam, you should focus on mastering key concepts in Plane Geometry, including understanding and calculating the properties of points, lines, angles, triangles, quadrilaterals, and circles. You should be able to solve problems involving area, perimeter, and volume, apply the Pythagorean theorem, and work with coordinate geometry. Additionally, practice identifying and working with various geometric transformations, such as rotations, translations, and reflections, to ensure a comprehensive understanding of Plane Geometry principles.

Key Concepts in Plane Geometry

Understanding the fundamental concepts of plane geometry is crucial for excelling in the ACT exam. This section will cover the essential elements such as points, lines, angles, triangles, quadrilaterals, and circles. By mastering these basics, you will be better prepared to tackle more complex problems and enhance your overall performance in the geometry portion of the ACT.

Points, Lines, and Angles

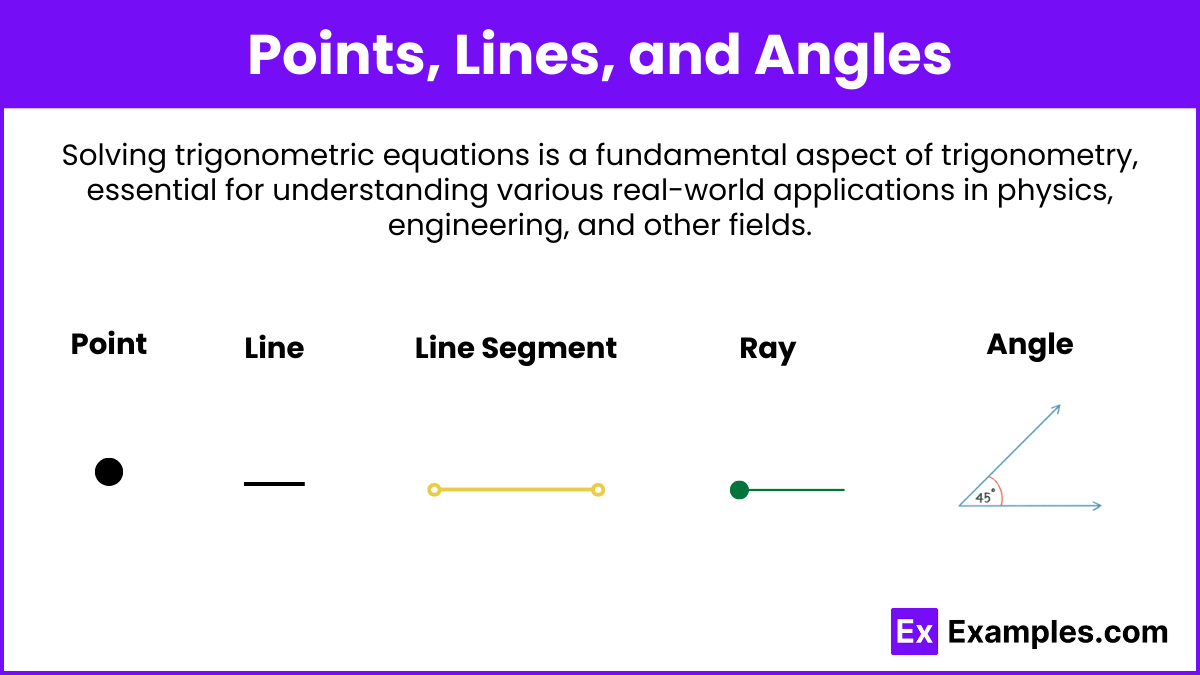
Point: A precise location in space, represented by a dot.
Line: A straight one-dimensional figure extending infinitely in both directions.
Line Segment: A part of a line bounded by two endpoints.
Ray: A part of a line that starts at one point and extends infinitely in one direction.
Angle: Formed by two rays with a common endpoint called the vertex. Measured in degrees.

Types of Angles

Angles are a fundamental concept in geometry, defined by the amount of turn between two straight lines that share a common endpoint called the vertex. Understanding the different types of angles is essential for solving various geometric problems and for practical applications in fields such as engineering and architecture.

Acute Angle: An acute angle is an angle that measures less than 90 degrees. These angles are small and sharp, often seen in various geometric shapes and designs.
Right Angle: A right angle is an angle that measures exactly 90 degrees. It forms a perfect “L” shape and is commonly found in squares, rectangles, and many other geometric figures.
Obtuse Angle: An obtuse angle is an angle that measures greater than 90 degrees but less than 180 degrees. These angles are wide and are often found in polygons such as obtuse triangles.
Straight Angle: A straight angle is an angle that measures exactly 180 degrees. It forms a straight line, effectively splitting the plane into two equal parts.

Triangles

Triangles have three sides and three angles. They are classified by sides as equilateral (all sides equal), isosceles (two sides equal), and scalene (all sides different). By angles, they are acute (all angles < 90°), right (one angle = 90°), and obtuse (one angle > 90°). The sum of interior angles is always 180°, and the Pythagorean theorem a²+b² = c² applies to right triangles.

Classification by Sides:
- Equilateral Triangle: All sides are equal.
- Isosceles Triangle: Two sides are equal.
- Scalene Triangle: All sides are different.
Classification by Angles:
- Acute Triangle: All angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.

Triangle Properties:

Sum of Angles: The sum of the interior angles of a triangle is always 180 degrees.
Pythagorean Theorem: In a right triangle, a²+b²=c², where ccc is the hypotenuse.

Quadrilaterals

Quadrilaterals are four-sided polygons with various properties based on their side lengths, angles, and parallelism. Understanding these properties helps in identifying and differentiating between different types of quadrilaterals.

Square: A square has four equal sides and four right angles. The diagonals bisect each other at right angles and are equal in length.
Rectangle: A rectangle has opposite sides that are equal and four right angles. The diagonals are equal in length and bisect each other.
Parallelogram: A parallelogram has opposite sides that are equal and parallel, and opposite angles are equal. The diagonals bisect each other but are not equal.
Rhombus: A rhombus has all sides equal, opposite sides are parallel, and opposite angles are equal. The diagonals bisect each other at right angles.
Trapezoid: A trapezoid has one pair of parallel sides. The non-parallel sides are called legs, and the height is the perpendicular distance between the parallel sides.

Circles

A circle is a simple geometric shape defined by all points that are equidistant from a central point called the center.

Radius: The distance from the center to any point on the circle.
Diameter: Twice the radius, the longest distance across the circle.
Circumference: The distance around the circle, C=2πr.
Area: The space inside the circle, A=πr².

Common Formulas in Plane Geometry

To effectively solve plane geometry problems on the ACT, it is crucial to have a firm grasp of the most commonly used formulas. These formulas allow you to calculate areas, perimeters, and other essential properties of various geometric shapes. Below are the key formulas you need to memorize and understand to excel in the ACT Math section.

Area Formulas

Triangle:
$A=\frac{1}{2} \times base \times height$
Rectangle:
$A=length \times width$
Square: A = side²
Parallelogram: A=base × height
Trapezoid:
$A=\frac{1}{2} \times \left(base₁ + base₂\right) \times height$
Circle: A=πr².

Perimeter Formulas

Triangle: Sum of all sides.

Rectangle: P=2×(length+width)

Square: P=4×side

Parallelogram: P=2×(base+side)

Circle (Circumference): C=2πr

Tips for Excelling in Plane Geometry on the ACT

Memorize Key Formulas: Ensure you know all the essential formulas for area, perimeter, and properties of shapes.
Practice Visualization: Draw diagrams to better understand and solve problems.
Review Geometry Basics: Refresh your knowledge of basic geometric principles and theorems.
Solve Practice Problems: Regularly practice ACT-style geometry questions to familiarize yourself with the format and types of questions asked.
Time Management: Practice solving geometry problems quickly and accurately to manage your time effectively during the exam.

Multiple Choice Questions for Plane Geometry

Question 1

What is the area of a triangle with a base of 10 units and a height of 6 units?

A. 30 square units
B. 60 square units
C. 20 square units
D. 15 square units

Answer: A

Explanation:
The area A of a triangle is calculated using the formula:

$A=\frac{1}{2} \times base \times height$

Substitute the given values:

$A=\frac{1}{2} \times 10 \times 6$

$A=\frac{1}{2} \times 60$

A = 30.

Therefore, the area of the triangle is 30 square units.

Question 2

Which of the following is true about a parallelogram? A. All four sides are equal and all angles are right angles.
B. Opposite sides are equal and parallel, and opposite angles are equal.
C. Only one pair of opposite sides is parallel.
D. Diagonals are always perpendicular to each other.

Answer: B

Explanation:
A parallelogram has the following properties:

Opposite sides are equal in length and parallel to each other.
Opposite angles are equal.
The diagonals bisect each other but are not necessarily perpendicular.

Option B correctly describes these properties. Option A describes a square, Option C describes a trapezoid, and Option D is not a property of parallelograms.

Question 3

What is the circumference of a circle with a radius of 4 units?

A. 8π units
B. 16π units
C. 4π units
D. 12π units

Answer: A

Explanation:
The circumference C of a circle is calculated using the formula:
C=2πr
where r is the radius of the circle. Substitute the given value:
C=2π×4
Therefore, the circumference of the circle is 8π units.