Asymptotes and Limits at Infinity

Last Updated: September 23, 2024

Notes

In AP Calculus, understanding asymptotes and limits at infinity is essential for analyzing the behavior of functions as they extend toward large positive or negative values. Asymptotes, which include horizontal, vertical, and oblique lines, represent boundaries that functions approach but never touch. Limits at infinity describe how functions behave as their input values grow infinitely large or small. Mastery of these concepts is crucial for graphing functions accurately and solving complex calculus problems on the AP exam.

Free AP Calculus AB Practice Test

Free AP Calculus BC Practice Test

Learning Objectives

In studying Asymptotes and Limits at Infinity for the AP Calculus exam, you should learn how to identify and analyze horizontal, vertical, and oblique asymptotes in functions. Understand how limits at infinity determine the end behavior of functions, and practice applying these concepts to various types of functions, including rational, polynomial, exponential, and logarithmic. Develop the ability to use limits to find asymptotes and accurately predict the behavior of graphs as 𝑥 approaches infinity or negative infinity. Master these skills to excel in problem-solving and graph interpretation.

Understanding Asymptotes

Asymptotes are lines that a graph approaches but does not intersect as it moves toward infinity. They give us insight into the behavior of functions at the extremes of their domains.

a) Horizontal Asymptotes

Horizontal asymptotes occur when the function approaches a constant value L as x approaches infinity (∞) or negative infinity (−∞). Mathematically, if:

$\left(\lim_{x \to \infty} f(x) = L \text{ or } \lim_{x \to -\infty} f(x) = L\right)$

Then, y = L is a horizontal asymptote.

Key Points:

Horizontal asymptotes indicate the end behavior of a function.
A function can cross its horizontal asymptote in its domain.
Rational functions often have horizontal asymptotes determined by the degrees of the numerator and denominator.

Example: For the function f(x) = x²+23x²+5:

$\left(f(x) = \frac{3x^2 + 5}{x^2 + 2} : \lim_{x \to \infty} \frac{3x^2 + 5}{x^2 + 2} = \lim_{x \to \infty} \frac{x^2(3 + \frac{5}{x^2})}{x^2(1 + \frac{2}{x^2})} = \frac{3}{1} = 3\right)$

Thus, y = 3 is the horizontal asymptote.

b) Vertical Asymptotes

Vertical asymptotes occur where a function approaches infinity or negative infinity as x approaches a specific value c. Formally, if:

$\left(\lim_{x \to c^+} f(x) = \pm\infty \text{ or } \lim_{x \to c^-} f(x) = \pm\infty\right)$

Then, x = c is a vertical asymptote.

Key Points:

Vertical asymptotes usually arise from undefined points in a function, such as zeros of the denominator in rational functions.
Unlike horizontal asymptotes, vertical asymptotes are never crossed by the function.

$\left(f(x) = \frac{1}{x - 2}, \, x = 2 \text{ is a vertical asymptote since: } \lim_{x \to 2^+} f(x) = \infty \text{ and } \lim_{x \to 2^-} f(x) = -\infty\right)$

c) Oblique (Slant) Asymptotes

Oblique or slant asymptotes occur when the degree of the numerator is exactly one higher than the degree of the denominator in a rational function. The slant asymptote is found by performing polynomial long division.

Example:

$\left(f(x) = \frac{x^2 + 3x + 2}{x - 1} : \text{ Long division: } x^2 + 3x + 2 \div (x - 1) \text{ gives } y = x + 4 \ldots\right)$

Limits at Infinity

Limits at infinity explore the behavior of a function as x approaches positive or negative infinity. These limits help determine the horizontal asymptotes of a function.

a) Polynomial Functions

For a polynomial function p(x)=anxn+an−1xn−1+⋯+a0:

$\left(\lim_{x \to \infty} p(x) = \infty \text{ if } a_n > 0\right)$
$\left(\lim_{x \to \infty} p(x) = -\infty \text{ if } a_n < 0\right)$

Example: For p(x)=2x³−4x²+1, as x→∞, the term 2x³ dominates, so:

$\left(\lim_{x \to \infty} p(x) = \infty\right)$

b) Rational Functions

For a rational function f(x)=q(x)p(x):

Degree of Numerator < Degree of Denominator: 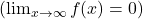$\left(\lim_{x \to \infty} f(x) = 0\right)$ . The horizontal asymptote is y=0.
Degree of Numerator = Degree of Denominator: $\left(\lim_{x \to \infty} f(x) = \frac{a_n}{b_n}\right)$
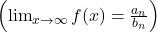
The horizontal asymptote is y=bnan.
Degree of Numerator > Degree of Denominator: The function has no horizontal asymptote. If the degree is exactly one higher, it has a slant asymptote.

c) Exponential and Logarithmic Functions

Exponential Functions f(x)=ex grow without bound as x approaches infinity: 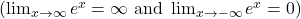$\left(\lim_{x \to \infty} e^x = \infty \text{ and } \lim_{x \to -\infty} e^x = 0\right)$ . Here, y=0 is the horizontal asymptote as x→−∞.
Logarithmic Functions f(x)=ln(x) increase without bound, but more slowly than polynomials:
$\left(\lim_{x \to \infty} \ln(x) = \infty \text{ and } \lim_{x \to 0^+} \ln(x) = -\infty\right)$

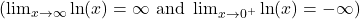
Analyzing Asymptotes and Limits at Infinity in Calculus Problems

a) Graphical Interpretation

Understanding the graphical behavior of functions is crucial. On the AP Calculus exam, you’ll often be asked to sketch graphs and identify asymptotes and end behavior based on limits at infinity.

b) Finding Asymptotes Using Limits

Use limits to determine where asymptotes occur:

Horizontal Asymptotes: Calculate $\left(\lim_{x \to \pm\infty} f(x)\right)$ .
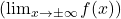Vertical Asymptotes: Look for points where the function tends to ±∞ as x approaches a finite value c.

c) L’Hôpital’s Rule

For indeterminate forms like $\left(\frac{\infty}{\infty} \text{ or } \frac{0}{0}\right)$ encountered in limits at infinity, L’Hôpital’s Rule is a powerful tool. Differentiate the numerator and denominator until the limit can be evaluated directly.

Examples

Example 1: Horizontal Asymptote in Rational Functions

Consider the function f(x)=x²−43x²+2x+1. As x approaches infinity, the lower-degree terms become negligible, and the function approaches the ratio of the leading coefficients. Thus, limx→∞f(x) = 13 = 3, indicating a horizontal asymptote at y=3.

Example 2: Vertical Asymptote and Limits

For the function g(x)=x−21, as x approaches 2, the function’s value grows without bound, either positively or negatively, depending on the direction. Specifically, limx→2+g(x)=∞ and limx→2−g(x)=−∞, showing a vertical asymptote at x=2.

Example 3: Oblique (Slant) Asymptote

Consider the function h(x) = x+1×2+3x+5. Dividing the numerator by the denominator gives a quotient of x+2, with a remainder that becomes negligible as x approaches infinity. Therefore, h(x) has an oblique asymptote given by the line y = x+2, and limx→∞(h(x)−(x+2)) = 0.

Example 4: Logarithmic Function and Horizontal Asymptote

The function f(x)=ln(x) exhibits a horizontal asymptote as x approaches infinity. The limit limx→∞ln(x) increases without bound, meaning there is no horizontal asymptote in this case. However, as x approaches 0 from the right, limx→0+ln(x)=−∞, showing that the x-axis acts as a horizontal asymptote for ln(x) at x near 0.

Example 5: Exponential Function and Limits at Infinity

For the function f(x) = e^−x, as x approaches infinity, the value of e^−x approaches 0. This indicates a horizontal asymptote at y = 0, with limx→∞e^−x = 0. Conversely, as x approaches negative infinity, limx→−∞e^−x=∞,

Multiple Choice Questions

Question 1

What is the horizontal asymptote of the function f(x)=5x²−72x²+3?

A) y = 0
B) y = 2/5
C) y = 5/2
D) There is no horizontal asymptote.

Answer: B) y = 2/5

Explanation: For a rational function like f(x) = 5x²−72x²+3, the horizontal asymptote is found by dividing the leading coefficients when the degrees of the numerator and denominator are the same. Here, the horizontal asymptote is y = 52.

Question 2

For the function f(x) = x−31, where is the vertical asymptote?

A) x=0
B) x=3
C) x=−3
D) There is no vertical asymptote.

Answer: B) x = 3

Explanation: A vertical asymptote occurs where the denominator is zero and the numerator is non-zero. For f(x) = x−31, the denominator becomes zero at x = 3. Therefore, the vertical asymptote is at x = 3.

Question 3

Evaluate the limit limx→∞2x+57x+1.

A) 7/2
B) 2/7
C) 1
D) 0

Answer: A) 7/2

Explanation: For the limit at infinity of a rational function 2x+57x+1, the limit is found by dividing the leading coefficients (7 from the numerator and 2 from the denominator). Therefore, limx→∞2x+57x+1=27.