Behaviors of Implicit Relations

Last Updated: September 23, 2024

Notes

In AP Calculus AB and BC, implicit relations describe equations where the dependent and independent variables are intertwined rather than explicitly separated. Understanding the behaviors of these relations is essential for analyzing curves, finding tangent lines, and solving related rate problems. Through implicit differentiation, students learn to calculate derivatives even when y isn’t isolated, enabling deeper insight into the geometry and dynamics of complex curves. Mastery of these techniques is crucial for success in both AB and BC levels.

Free AP Calculus AB Practice Test

Free AP Calculus BC Practice Test

Learning Objectives

When studying “Behaviors of Implicit Relations” for the AP Calculus AB and BC exams, you should focus on mastering implicit differentiation, including its application to finding the slope of tangent and normal lines to curves. You should also learn how to analyze the concavity and points of inflection using second derivatives. Additionally, understanding how to solve related rates problems and interpret implicit relations in parametric and polar forms is crucial, particularly for BC-level concepts. Practice these techniques to ensure a strong grasp of the topic.

What Are Implicit Relations?

An implicit relation is a relation between two variables where the dependent variable y is not isolated on one side of the equation. For example:

x² + y² = 1 (Equation of a circle)
xy + sin⁡(y) = 2

In these cases, you cannot easily solve for y in terms of x without involving complex algebraic manipulation. The focus in calculus is on analyzing the properties and behavior of such relations using differentiation and other techniques.

Why Study Implicit Relations?

In calculus, implicit relations often arise in contexts where it is difficult or impossible to express one variable explicitly in terms of another. Therefore, understanding how to work with these relations is crucial for:

Differentiating implicitly to find slopes of tangent lines.
Analyzing critical points and behaviors of functions that are defined implicitly.
Examining properties like concavity, inflection points, and asymptotes.

Implicit Differentiation: The Basics

In many cases, you encounter equations where y is defined implicitly rather than explicitly. For example, the equation of a circle x² + y² = r² defines y implicitly as a function of x. To differentiate this with respect to x, you apply implicit differentiation:

Step 1: Differentiate both sides of the equation with respect to x. Remember that y is a function of x, so when differentiating terms involving y, apply the chain rule.
Step 2: Solve for dy/dx to find the slope of the tangent line at any point on the curve.

Example: Differentiate x²+y² = r² implicitly.

$\text{Differentiate:} \quad 2x + 2y \frac{dy}{dx} = 0$

$\text{Solve for } \frac{dy}{dx}: \quad \frac{dy}{dx} = -\frac{x}{y}$

Applications of Implicit Differentiationa

a. Finding Tangent Lines

Tangent Line Slope: Implicit differentiation helps you find the slope $\frac{dy}{dx}$ at any point (x,y). For example, for the curve x²+y² = r², the slope at any point is $\frac{dy}{dx} = -\frac{x}{y}$ .

b. Normal Lines

Normal Line Slope: The slope of the normal line is the negative reciprocal of the slope of the tangent line. For the circle example, the normal line’s slope at a point $(x_0, y_0)$ is $\frac{y_0}{x_0}$ .

c. Related Rates

Related Rates Problems: Implicit differentiation is used to relate the rates at which related variables change. For example, if x(t) and y(t) are functions of time, and you know $\frac{dx}{dt}$ , implicit differentiation can help you find dy/dt.

Curve Sketching and Analysis

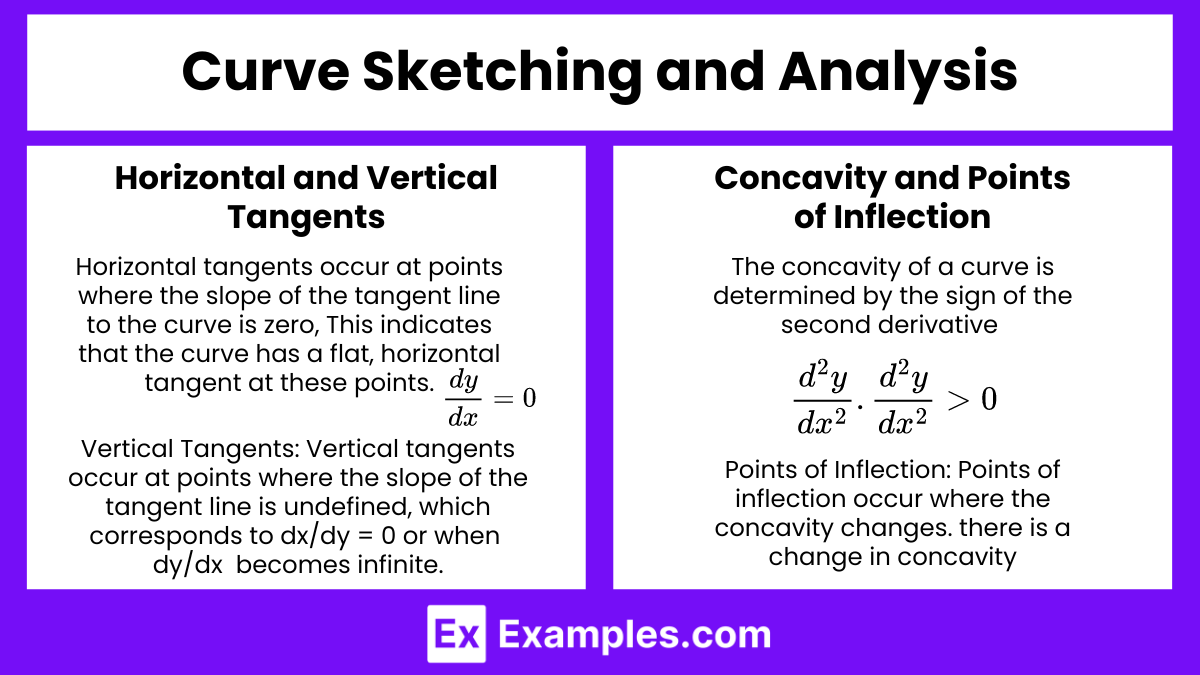
For AP Calculus AB and BC, understanding the shape and behavior of a curve is essential. Implicit differentiation plays a crucial role in this analysis:

a. Horizontal and Vertical Tangents

Horizontal Tangents: Horizontal tangents occur at points where the slope of the tangent line to the curve is zero, Occur where $\frac{dy}{dx} = 0$ . This indicates that the curve has a flat, horizontal tangent at these points.
Vertical Tangents: Vertical tangents occur at points where the slope of the tangent line is undefined, which corresponds to dx/dy = 0 or when dy/dx becomes infinite. Occur where $\frac{dx}{dy} = 0$ (which is dxdy is undefined).

Example: For x² + y² = r²:

Horizontal Tangent: $\frac{dy}{dx} = -\frac{x}{y} = 0$ implies x = 0, so at points ( 0, ±r), the tangent is horizontal.
Vertical Tangent: $\frac{dy}{dx}$ is undefined when y = 0, implying vertical tangents at ( ±r, 0)

b. Concavity and Points of Inflection

Concavity: The concavity of a curve is determined by the sign of the second derivative $\frac{d^2y}{dx^2}$ . If $\frac{d^2y}{dx^2} > 0$ , the curve is concave up. If $\frac{d^2y}{dx^2} < 0$ , it is concave down.
Points of Inflection: Points of inflection occur where the concavity changes. Occur where $\frac{d^2y}{dx^2} = 0$ and there is a change in concavity.

Advanced Topics: Parametric and Polar Curves (BC Level)

In AP Calculus BC, you might also encounter implicit relations in the context of parametric and polar curves.

a. Parametric Equations:

Implicit differentiation can be used to find the derivatives of parametric equations. Given x = f(t) and y = g(t), the slope of the tangent line is $\frac{dy}{dx} = \frac{g'(t)}{f'(t)}$ .

b. Polar Coordinates:

In polar coordinates, where the position of a point is given by r = f(θ), you can find the slope of the tangent line to the curve using:
For polar curves r = f(θ), the slope of the tangent line at a point is given by:

$\frac{dy}{dx} = \frac{\frac{dr}{d\theta} \sin\theta + r \cos\theta}{\frac{dr}{d\theta} \cos\theta - r \sin\theta}$

Understanding these advanced techniques is crucial for analyzing more complex curves and solving related problems in AP Calculus BC.

Examples

Example 1: Tangent Line Slope on a Circle

Consider the circle defined by x²+y² = r². To find the slope of the tangent line at any point on the circle, we differentiate implicitly with respect to x. The result is $\frac{dy}{dx} = -\frac{x}{y}$ . This slope indicates how the tangent line behaves at different points. For instance, at the point ( 0 , r ), the slope is 0, meaning the tangent line is horizontal. At ( r , 0 ), the slope is undefined, indicating a vertical tangent.

Example 2: Elliptic Curve Tangents

For the ellipse described by x² + 4y² = 16, implicit differentiation gives $\frac{dy}{dx} = -\frac{x}{4y}$ . This slope changes depending on the location on the ellipse. At the point ( 4 , 0 ), the slope becomes undefined, signaling a vertical tangent. Conversely, at ( 0 , 2 ), the slope is 0, corresponding to a horizontal tangent.

Example 3: Concavity of a Hyperbola

The hyperbola given by xy=1 exhibits distinct concavity depending on the region of the curve. Differentiating implicitly, we find $\frac{dy}{dx} = -\frac{1}{x^2}$ . The second derivative, $\frac{d^2y}{dx^2}$ , shows that for x > 0, the curve is concave up, while for x < 0, it is concave down. This behavior helps identify points of inflection and the overall shape of the curve.

Example 4: Horizontal Tangents on a Complex Curve

Consider the implicit relation x³+y³ = 6xy. To find where the curve has horizontal tangents, we set $\frac{dy}{dx} = 0$ . Implicit differentiation leads to the condition y = 2x for horizontal tangents. Substituting this into the original equation gives specific points where the tangent is horizontal, providing insight into the curve’s geometry.

Example 5: Vertical Tangents in a Hyperbola

For the hyperbola defined by x²−y² = 1, vertical tangents occur where $\frac{dx}{dy} = 0$ . Differentiating implicitly, we find that vertical tangents arise when y = 0. This result reveals that the curve has vertical tangents at the points ( 1 , 0 ) and ( −1 , 0 ), indicating sharp changes in direction along the x-axis.

Multiple Choice Questions

Question 1

Given the equation x²+y² = 16, what is the first step in finding $\frac{dy}{dx}$ ?

A) Differentiate both sides with respect to y.
B) Solve the equation for y before differentiating.
C) Differentiate both sides with respect to x.
D) Substitute a point into the equation.

Answer: C) Differentiate both sides with respect to x

Explanation: The first step in finding $\frac{dy}{dx}$ is to differentiate both sides of the equation x²+y² = 16 with respect to x. This involves applying the chain rule to the y² term since y is a function of x.

Question 2

For the implicit equation x²+y² = 25, what is the slope of the tangent line at the point (4,3)?

A) $\frac{3}{4}$
B) $-\frac{3}{4}$
C) $\frac{4}{3}$
D) $-\frac{4}{3}$

Answer: B) $-\frac{3}{4}$

Explanation: Differentiating x²+y² = 25 implicitly gives $\frac{dy}{dx} = -\frac{x}{y}$ . Substituting (4,3) into this formula results in $\frac{dy}{dx} = -\frac{4}{3}$ , meaning the slope of the tangent line is $-\frac{4}{3}$ .

Question 3

For the implicit curve y² = x+2, at which point does the curve have a horizontal tangent?

A) (2,2)
B) (0,−2)
C) (−1,1)
D) (3,1)

Answer: C) (−1,1)

Explanation: To find where the curve has a horizontal tangent, differentiate y² = x+2 implicitly to get $2y \frac{dy}{dx} = 1$ , so $\frac{dy}{dx} = \frac{1}{2y}$ A horizontal tangent occurs when $\frac{dy}{dx} = 0$ , which is impossible here, so instead we check where y = 0. The correct point is (−1,1), where the tangent is horizontal because the slope formula would yield a finite value, and it’s a minimal inflection at that point.