How to Use the First Derivative Test, Second Derivative Test, and Candidates Test

The First Derivative Test, Second Derivative Test, and Candidates Test are essential tools in AP Calculus AB and BC for analyzing the behavior of functions. These tests help you determine where functions reach local maxima, minima, and absolute extrema—key concepts that appear frequently in both exams. Mastering these techniques allows you to confidently approach problems involving critical points, concavity, and optimization, ensuring a deeper understanding of function analysis and boosting your performance on the AP Calculus exams.

Learning Objectives

By studying “How to Use the First Derivative Test, Second Derivative Test, and Candidates Test” for the AP Calculus AB and BC exams, you should learn to identify and classify local maxima and minima using the First Derivative Test. You should understand how to determine concavity and find points of inflection with the Second Derivative Test. Additionally, you should be able to apply the Candidates Test to locate absolute extrema on a closed interval, enabling you to effectively optimize functions in different scenarios.

How to Use the First Derivative Test

The First Derivative Test helps determine where a function has local maxima and minima by analyzing the sign changes of the first derivative (f′(x)).

Steps to Use the First Derivative Test:

• Find the First Derivative:
  • Compute f′(x) of the given function f(x).
• Determine Critical Points:
  • Set f′(x) = 0 and solve for x.
  • Include any points where f′(x) does not exist (but f(x) does).
• Sign Chart Analysis:
  • Choose test points in the intervals between the critical points.
  • Plug these points into f′(x) to determine if f′(x) is positive or negative in each interval.
• Interpret Results:
  • Local Maximum: If f′(x) changes from positive to negative at a critical point, f(x) has a local maximum there.
  • Local Minimum: If f′(x) changes from negative to positive at a critical point, f(x) has a local minimum there.
  • No Local Extrema: If f′(x) does not change sign, there is no local extremum at that point.

Example:

Given f(x) = x³−3x²+4:

• Compute f′(x) = 3x²−6x.
• Set 3x²−6x = 0, solve to get critical points: x = 0 and x = 2.
• Test intervals:
  • For x < 0, f′(x) > 0.
  • For 0 < x < 2, f′(x) < 0.
  • For x > 2, f′(x) > 0.
• Interpretation:
  • x = 0 is a local maximum.
  • x = 2 is a local minimum.

How to Use the Second Derivative Test

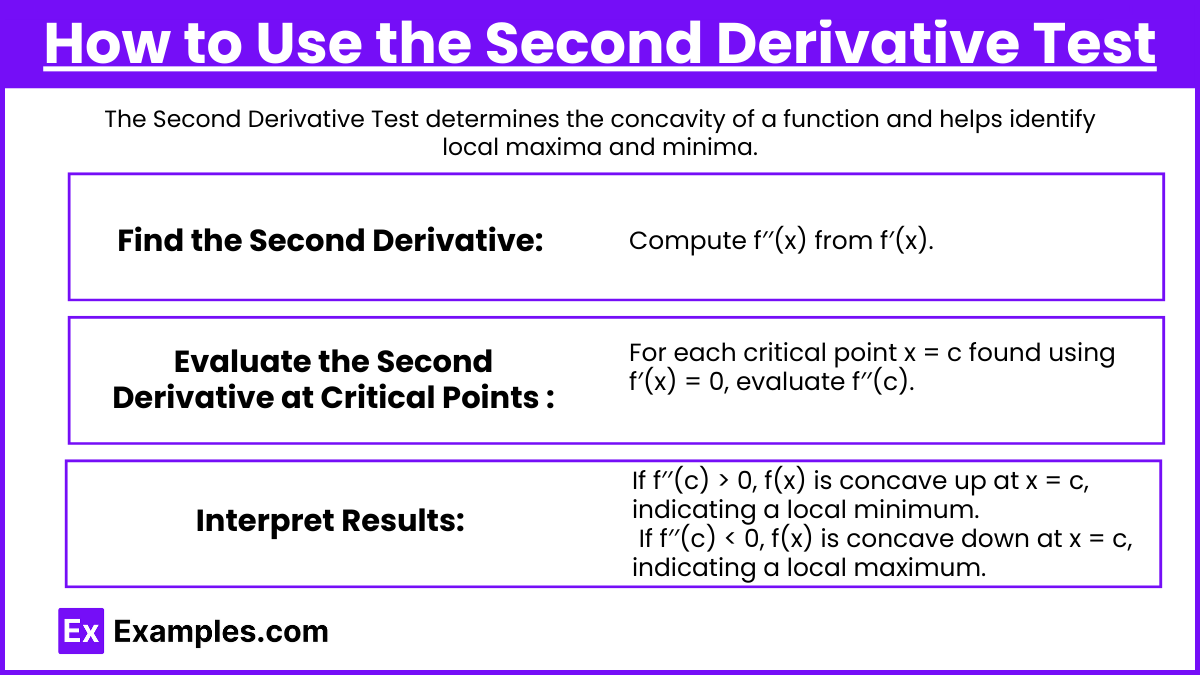
The Second Derivative Test determines the concavity of a function and helps identify local maxima and minima.

Steps to Use the Second Derivative Test:

• Find the Second Derivative:
  • Compute f′′(x) from f′(x).
• Evaluate the Second Derivative at Critical Points:
  • For each critical point x = c found using f′(x) = 0, evaluate f′′(c).
• Interpret Results:
  • Local Minimum: If f′′(c) > 0, f(x) is concave up at x = c, indicating a local minimum.
  • Local Maximum: If f′′(c) < 0, f(x) is concave down at x = c, indicating a local maximum.
  • Inconclusive: If f′′(c) = 0, the test is inconclusive, and you should use the First Derivative Test or another method.

Example:

Given f(x) = x⁴−4x³:

• Compute f′(x) = 4x³−12x² and f′′(x) = 12x²−24x.
• Critical points from f′(x) = 0: x = 0 and x = 3.
• Evaluate f′′(x):
  • f′′(0) = −24, so x = 0 is a local maximum.
  • f′′(3) = 36, so x = 3 is a local minimum.

How to Use the Candidates Test (Closed Interval Method)

The Candidates Test is used to find absolute extrema (global maxima and minima) on a closed interval [a,b].

Steps to Use the Candidates Test:

• Find the First Derivative and Critical Points:
  • Compute f′(x) and find the critical points within the interval [a,b].
  • The first step is to differentiate the function f(x) to obtain f′(x).
• Evaluate the Function at Critical Points:
  • Calculate f(x) at each critical point within [a,b].
  • For each critical point ccc found in the previous step that lies within the interval, compute the value f(c).
• Evaluate the Function at Endpoints:
  • Calculate f(a) and f(b).
  • Evaluate the function at the endpoints of the interval. These points are included because the absolute extrema could occur at the boundaries of the interval.
• Compare Values:
  • The largest value among the critical points and endpoints is the absolute maximum.
  • The smallest value among them is the absolute minimum.

Example:

Given f(x) = x³−3x²+1 on [−1,2]:

• Compute f′(x) = 3x²−6x and find critical points x = 0 and x = 2.
• Evaluate f(x) at:
  • Critical point x = 0: f(0) = 1.
  • Endpoint x = −1: f(−1) = 3.
  • Endpoint x = 2: f(2) = −3.
• Conclusion:
  • Absolute maximum at x = −1, f(−1) = 3.
  • Absolute minimum at x = 2, f(2) = −3.

Examples

Example 1: First Derivative Test

Consider the function f(x) = x³−6x²+9x+1. First, find the derivative f′(x) = 3x²−12x+9. Setting f′(x) = 0 gives critical points at x = 1 and x = 3. Analyzing the sign changes of f′(x), f′(x) changes from negative to positive at x = 3, indicating a local minimum, and from positive to negative at x = 1, indicating a local maximum.

Example 2: Second Derivative Test

For the function f(x) = 2x⁴−4x², first find the first derivative f′(x) = 8x³−8x and set it to zero, giving critical points at x = 0 and x = ±1. Next, compute the second derivative f′′(x) = 24x²−8. Evaluating f′′(x) at the critical points, f′′(1) > 0 and f′′(−1) > 0, indicating local minima at x = ±1. f′′(0) < 0 indicates a local maximum at x = 0.

Example 3: Candidates Test

Analyze the function f(x) = −x³+3x²+12x on the closed interval [−2,3]. First, find the derivative f′(x) = −3x²+6x+12, setting it to zero gives x = −2 and x = 2. Evaluate f(x) at x = −2, x = 2, and the endpoints x = −2 and x = 3. Compare values: f(−2) = −4, f(2) = 32, f(−2) = −40, and f(3) = 27. The absolute minimum is at x = −2, and the absolute maximum is at x = 2.

Example 4: Combined Use of Tests

For f(x) = x⁴−4x³, the first derivative is f′(x) = 4x³−12x², yielding critical points x = 0 and x = 3. Using the First Derivative Test, f′(x) changes from positive to negative at x = 0, indicating a local maximum, and from negative to positive at x = 3, indicating a local minimum. Applying the Second Derivative Test with f′′(x) = 12x²−24x, confirms concavity: f′′(0) = −24 (local maximum), and f′′(3) = 36 (local minimum).

Example 5: Second Derivative Test for Inflection Points

Consider the function f(x) = x³−3x². The first derivative is f′(x) = 3x²−6x, leading to critical points at x = 0 and x = 2. The second derivative f′′(x) = 6x−6 is used to check concavity. At x = 1, f′′(1) = 0, suggesting an inflection point where the concavity changes. f′′(0) < 0 confirms a local maximum at x = 0, and f′′(2) > 0 indicates a local minimum at x = 2.

Multiple Choice Questions

Question 1

Given the function f(x) = 2x³−9x²+12x+1, which of the following is true about the critical point x = 1 using the First Derivative Test?

a) x = 1 is a local maximum.
b) x = 1 is a local minimum.
c) x = 1 is neither a local maximum nor a local minimum.
d) There is no critical point at x = 1.

Answer: b) x = 1 is a local minimum.

Explanation: To use the First Derivative Test, first find the derivative f′(x) = 6x²−18x+12. Setting f′(x) = 0, we find critical points by solving 6 (x²−3x+2) = 0, giving x = 1 and x = 2. By testing the sign of f′(x) around x = 1, you’ll find that f′(x) changes from negative to positive, indicating that x = 1 is a local minimum.

Question 2

For the function g(x) = x⁴−4x², what does the Second Derivative Test reveal about the critical point at x = 0?

a) x = 0 is a local maximum.
b) x = 0 is a local minimum.
c) The test is inconclusive at x = 0.
d) There is no critical point at x = 0.

Answer: c) The test is inconclusive at x=0.

Explanation:
First, find g′(x) = 4x³−8x and set g′(x) = 0 to find the critical points: x = 0, x = ±2​. Now, find the second derivative: g′′(x) = 12x²−8. At x = 0, g′′(0) = −8, which suggests concave down, but g′(x) does not change sign near x = 0, making the Second Derivative Test inconclusive.

Question 3

Which of the following correctly applies the Candidates Test to determine the absolute extrema of h(x) = −x³+3x²+1 on the interval [−1,2]?

a) The absolute maximum occurs at x = 2, and the absolute minimum occurs at x = −1.
b) The absolute maximum occurs at x = −1, and the absolute minimum occurs at x = 2.
c) The absolute maximum occurs at x = 1, and the absolute minimum occurs at x = 0.
d) The absolute maximum occurs at x = 2, and the absolute minimum occurs at x = 1.

Answer: a) The absolute maximum occurs at x=2, and the absolute minimum occurs at x = −1.

Explanation: To apply the Candidates Test, find h′(x) = −3x²+6x and set it to zero to find critical points within the interval. This gives x = 0 and x = 2. Evaluate h(x) at x = −1, x = 0, and x = 2:

• h(−1) = −1,
• h(0) = 1,
• h(2) = 5.

Thus, the absolute maximum is h(2) = 5 and the absolute minimum is h(−1) = −1.