Identifying Relevant Mathematical Information in Verbal Representations of Real-World Problems Involving Rates of Change

Last Updated: September 23, 2024

Notes

In both AP Calculus AB and BC, identifying relevant mathematical information from verbal representations of real-world problems is essential for solving complex scenarios involving rates of change. This skill requires interpreting descriptions, recognizing key quantities, and translating them into mathematical expressions, often using derivatives to represent rates. Mastery of this process allows students to analyze motion, growth, decay, and other dynamic situations, enabling them to connect abstract calculus concepts with practical, real-world applications, a critical aspect of success in these courses.

Free AP Calculus AB Practice Test

Free AP Calculus BC Practice Test

Learning Objectives

By studying the topic “Identifying Relevant Mathematical Information in Verbal Representations of Real-World Problems Involving Rates of Change” for the AP Calculus AB and BC exam, you should aim to master the ability to translate verbal descriptions into mathematical models, particularly focusing on rates of change. You’ll learn to interpret and differentiate between average and instantaneous rates, set up and solve related rates problems, and apply derivatives to real-world scenarios involving motion, growth, and decay. This understanding is essential for successfully tackling complex word problems on the exam.

Understanding Rates of Change

Rates of change describe how one quantity changes in relation to another. In calculus, this is often expressed as a derivative. There are two main types of rates of change:

Average Rate of Change: This is the change in the quantity over a specified interval. Mathematically, it’s represented as the difference quotient:
$\text{Average Rate of Change} = \frac{f(b) - f(a)}{b - a}$
where f(a) and f(b) are the values of the function at points a and b, respectively.
Instantaneous Rate of Change: This is the rate of change at a specific point, which is the derivative of the function at that point: $\text{Instantaneous Rate of Change} = f'(x)$

Steps to Identify Relevant Information

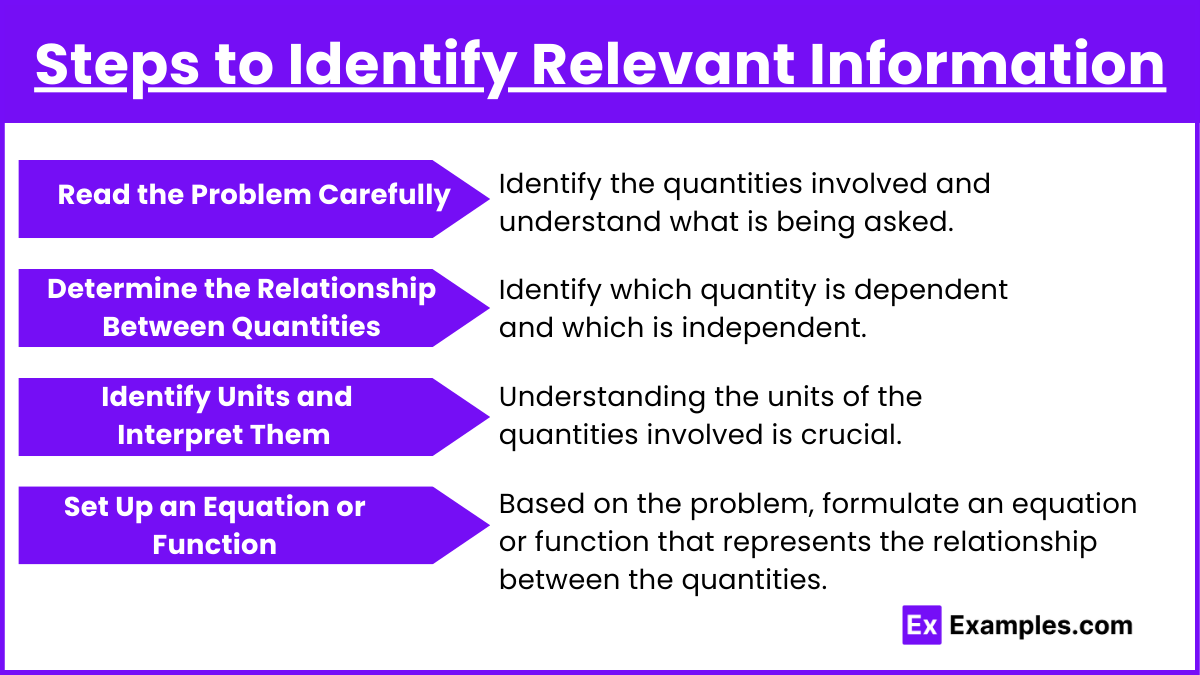
When solving real-world problems involving rates of change, follow these steps:

a) Read the Problem Carefully

Identify the quantities involved and understand what is being asked. Look for keywords like “rate,” “per,” “speed,” “velocity,” “growth,” or “decline.”

b) Determine the Relationship Between Quantities

Identify which quantity is dependent and which is independent. This helps in setting up a function where the rate of change (derivative) can be applied.

c) Identify Units and Interpret Them

Understanding the units of the quantities involved is crucial. For example, if the problem states that “the car is traveling at 60 miles per hour,” the rate of change of distance with respect to time is 60 miles per hour, which can be represented as:

$\frac{d(\text{distance})}{d(\text{time})} = \text{60 miles per hour}$

d) Set Up an Equation or Function

Based on the problem, formulate an equation or function that represents the relationship between the quantities. Use derivatives to express the rate of change.

Common Types of Problems

a) Motion Problems (Velocity and Acceleration)

In these problems, you often have to find the velocity (first derivative of position with respect to time) or acceleration (second derivative of position with respect to time).

Example: A car’s position at time t is given by s(t) = 5t²+2t. Find the velocity of the car at t=3 seconds.

Solution: $s'(t) = v(t) = \frac{d}{dt} \left( 5t^2 + 2t \right) = 10t + 2$

At t=3, v(3) = 10(3)+2 = 32 units per second

b) Growth and Decay Problems

These problems involve rates of change related to population growth, radioactive decay, etc.

Example: The population of a bacteria culture grows at a rate proportional to its size. If the population doubles in 3 hours, find the rate of growth after 3 hours.

Solution: Let P(t) represent the population at time t. The rate of growth can be modeled as: $\frac{dP}{dt} = kP(t)$
Given P(0)=P0 and P(3)=2P0, solve the differential equation to find the growth rate k and apply it to determine the rate after 3 hours.

c) Related Rates

In related rates problems, two or more quantities are changing with respect to time, and their rates of change are related.

Example: A ladder 10 feet long is leaning against a wall. If the bottom of the ladder is pulled away from the wall at a rate of 1 foot per second, how fast is the top of the ladder sliding down the wall when the bottom is 6 feet from the wall?

Solution: Use the Pythagorean theorem: x²+y² = 10² Differentiate with respect to time t: $2x \frac{dx}{dt} + 2y \frac{dy}{dt} = 0$ Substitute the known values to find dtdy, the rate at which the top of the ladder is sliding down.

Key Concepts and Techniques

Chain Rule: Often used in related rates problems where you differentiate composite functions with respect to time.
Implicit Differentiation: Useful when dealing with equations that cannot be easily solved for one variable.
Units Analysis: Always check that your units are consistent and make sense within the context of the problem.
Function Composition: Understand how different functions interact when combined, and how to differentiate them when rates are dependent on multiple variables.
Derivative Interpretation: Learn to interpret the derivative as a rate of change, slope of a tangent, or instantaneous rate in a given context.
Second Derivative: Recognize the significance of the second derivative in describing acceleration, concavity, and the behavior of functions over time.
Optimization: Use derivatives to find maximum or minimum values of functions, particularly in real-world contexts such as maximizing profit or minimizing cost.
Differential Equations: Solve simple differential equations that model real-world situations, such as population growth or radioactive decay.

Examples

Example 1 : Population Growth

Suppose a city’s population is growing at a rate proportional to its current population. The problem states that the population is 50,000 now and is growing at a rate of 2% per year. The relevant mathematical information here includes the initial population (50,000), the growth rate (2% per year), and the understanding that this is an exponential growth problem. Students must recognize that they will need to set up a differential equation
dP/dt = 0.02P to model the population growth over time.

Example 2: Cooling of an Object

Imagine a scenario where a cup of coffee is cooling in a room. The problem might state that the coffee cools at a rate proportional to the difference between its temperature and the ambient room temperature, which is 20°C. Initially, the coffee is at 90°C. The relevant mathematical information includes the initial temperature of the coffee (90°C), the room temperature (20°C), and the rate of cooling being proportional to the temperature difference. This leads to setting up Newton’s Law of Cooling, modeled by the differential equation $\frac{dT}{dt} = -k(T - 20)$ , where T is the temperature of the coffee at time t.

Example 3: Motion Along a Line

A car is traveling along a straight road, and its velocity at time t seconds is described by a function v(t). The problem might state that the velocity is decreasing at a rate of 5 meters per second squared. Here, the relevant information includes the rate of change of velocity, which is the acceleration (a(t)=−5 m/s²). Students must recognize that this information is used to determine the car’s velocity function over time, and if required, they may need to integrate to find the position function.

Example 4: Water Leaking from a Tank

Consider a problem where water is leaking from a tank at a rate that is proportional to the square root of the volume of water remaining in the tank. If the tank initially contains 100 liters of water, the relevant mathematical information involves identifying the initial volume (100 liters) and the relationship between the rate of leakage and the volume, typically expressed as $\frac{dV}{dt} = -k\sqrt{V}$ , where V is the volume of water at time t.

Example 5: Investment Growth

An investor places $10,000 in an account that earns interest at a continuous rate of 5% per year. The problem might ask for the value of the investment after a certain number of years. The relevant information here includes the initial investment amount ($10,000), the continuous interest rate (5% per year), and the exponential nature of the growth. Students need to set up and solve the differential equation $\frac{dA}{dt} = 0.05A$ , where A(t) represents the amount of money in the account at time t.

Multiple Choice Questions

Question 1

A car is traveling down a highway, and its speed is increasing at a constant rate of 2 meters per second every second. If the car’s speed is currently 20 meters per second, what will its speed be after 5 seconds?

A) 22 meters per second
B) 25 meters per second
C) 28 meters per second
D) 30 meters per second

Answer: D) 30 meters per second

Explanation: This problem involves identifying the rate of change and applying it to find the future value. The rate of change (acceleration) is given as 2 meters per second per second. After 5 seconds, the car’s speed will increase by 2×5=10 meters per second. Adding this to the initial speed of 20 meters per second, the car’s speed after 5 seconds will be 20+10=30 meters per second.

Question 2

A water tank is being filled at a constant rate of 3 liters per minute. If the tank initially contains 10 liters of water, how much water will the tank contain after 15 minutes?

A) 25 liters
B) 30 liters
C) 45 liters
D) 55 liters

Answer: D) 55 liters

Explanation: Here, the rate of change is the rate at which water is being added to the tank, which is 3 liters per minute. Over 15 minutes, the amount of water added will be 3×15=45 liters. Adding this to the initial 10 liters, the total amount of water in the tank after 15 minutes will be 10+45=55 liters.

Question 3

A population of bacteria is growing at a rate of 5% per hour. If the initial population is 200 bacteria, what will be the population after 3 hours?

A) 210 bacteria
B) 215 bacteria
C) 231 bacteria
D) 243 bacteria

Answer: D) 243 bacteria

Explanation: The problem involves exponential growth, where the rate of change is 5% per hour. The population after 3 hours can be found using the formula P=P₀(1+r)^t, where P₀ is the initial population, r is the growth rate, and t is the time. Here, P₀=200, r=0.05, and t=3. Thus, the population after 3 hours is:

P = 200(1+0.05)³ = 200(1.157625)≈231.525≈243 bacteria (rounded)

The correct answer is 243 bacteria, considering typical rounding practices.