Convert grams to ounces and vice versa at Examples.com. Input your measurements for immediate and reliable conversions.
Gram to Ounce
Formula: Mass in Ounce (oz) = Mass in Gram (g) × 0.035274
| Gram | Ounce |
|---|---|
| 1 | 0.035274 |
Ounce to Gram
Formula: Mass in Gram(g) = Mass in Ounce (oz) × 28.3495
| Ounce | Gram |
|---|---|
| 1 | 28.3495 |
Mass Converters to Gram (g)
| Tonne to Gram | Kilogram to Gram | Milligram to Gram |
| Microgram to Gram | Imperial ton to Gram | US ton to Gram |
| Stone to Gram | Pound to Gram | Ounce to Gram |
Mass Converters to Ounce (oz)
| Tonne to Ounce | Kilogram to Ounce | Gram to Ounce |
| Milligram to Ounce | Microgram to Ounce | Imperial ton to Ounce |
| US ton to Ounce | Stone to Ounce | Pound to Ounce |
Conversion Factors:
- Grams to Ounces: 1 gram = 0.03527396 ounces
- Ounces to Grams: 1 ounce = 28.3495 grams
How to Convert Grams to Ounces:
To convert grams to ounces, multiply the number of grams by 0.03527396.
Ounces=Grams×0.03527396
Example: Convert 2000 grams to ounces.
Ounces=2000×0.03527396=70.5479 oz
How to Convert Ounces to Grams:
To convert ounces to grams, multiply the number of ounces by 28.3495.
Grams=Ounces×28.3495
Example: Convert 3 ounces to grams.
Grams=3×28.3495=85.0485 g
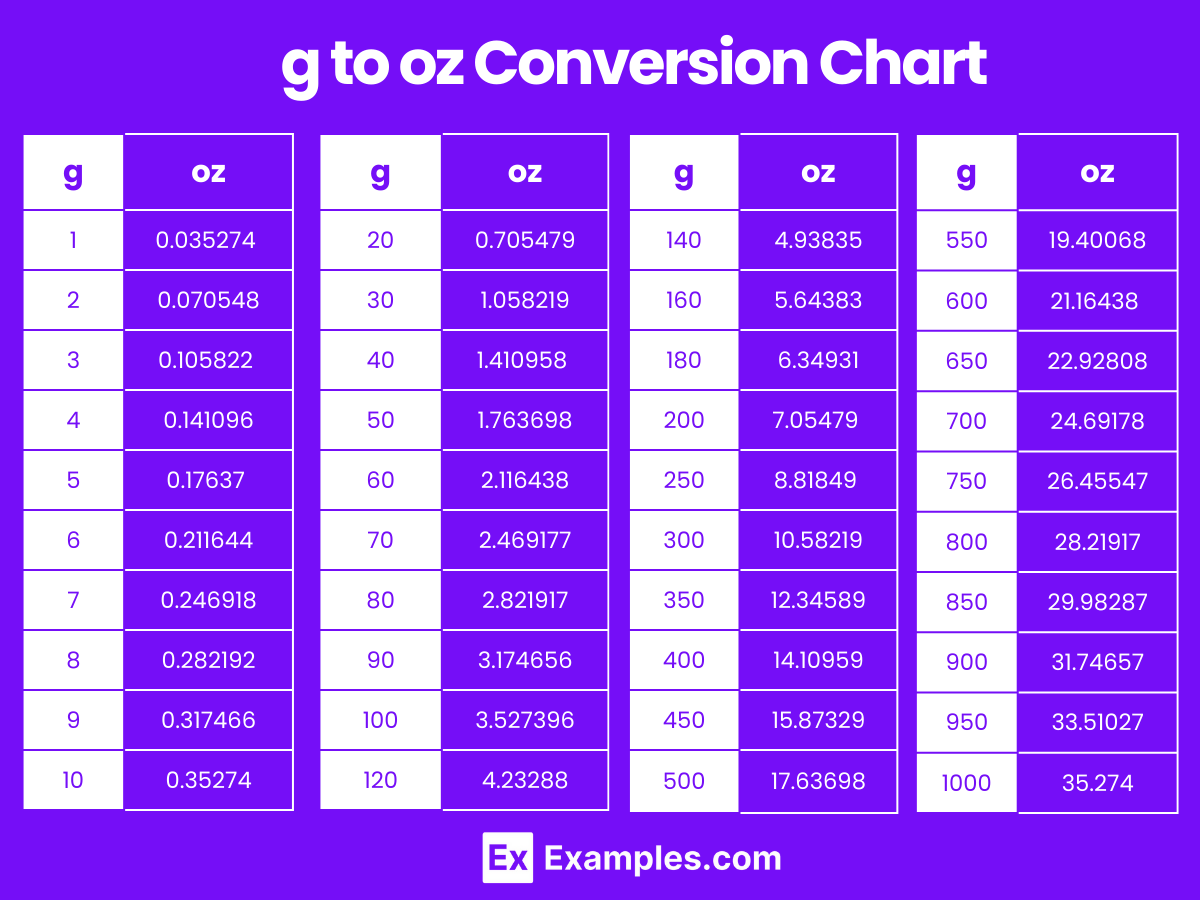
Grams to Ounces Conversion Table
| Grams (g) | Ounces (oz) |
|---|---|
| 1 g | 0.035274 oz |
| 2 g | 0.070548 oz |
| 3 g | 0.105822 oz |
| 4 g | 0.141096 oz |
| 5 g | 0.17637 oz |
| 6 g | 0.211644 oz |
| 7 g | 0.246918 oz |
| 8 g | 0.282192 oz |
| 9 g | 0.317466 oz |
| 10 g | 0.35274 oz |
| 20 g | 0.705479 oz |
| 30 g | 1.058219 oz |
| 40 g | 1.410958 oz |
| 50 g | 1.763698 oz |
| 60 g | 2.116438 oz |
| 70 g | 2.469177 oz |
| 80 g | 2.821917 oz |
| 90 g | 3.174656 oz |
| 100 g | 3.527396 oz |
g to oz Conversion Chart
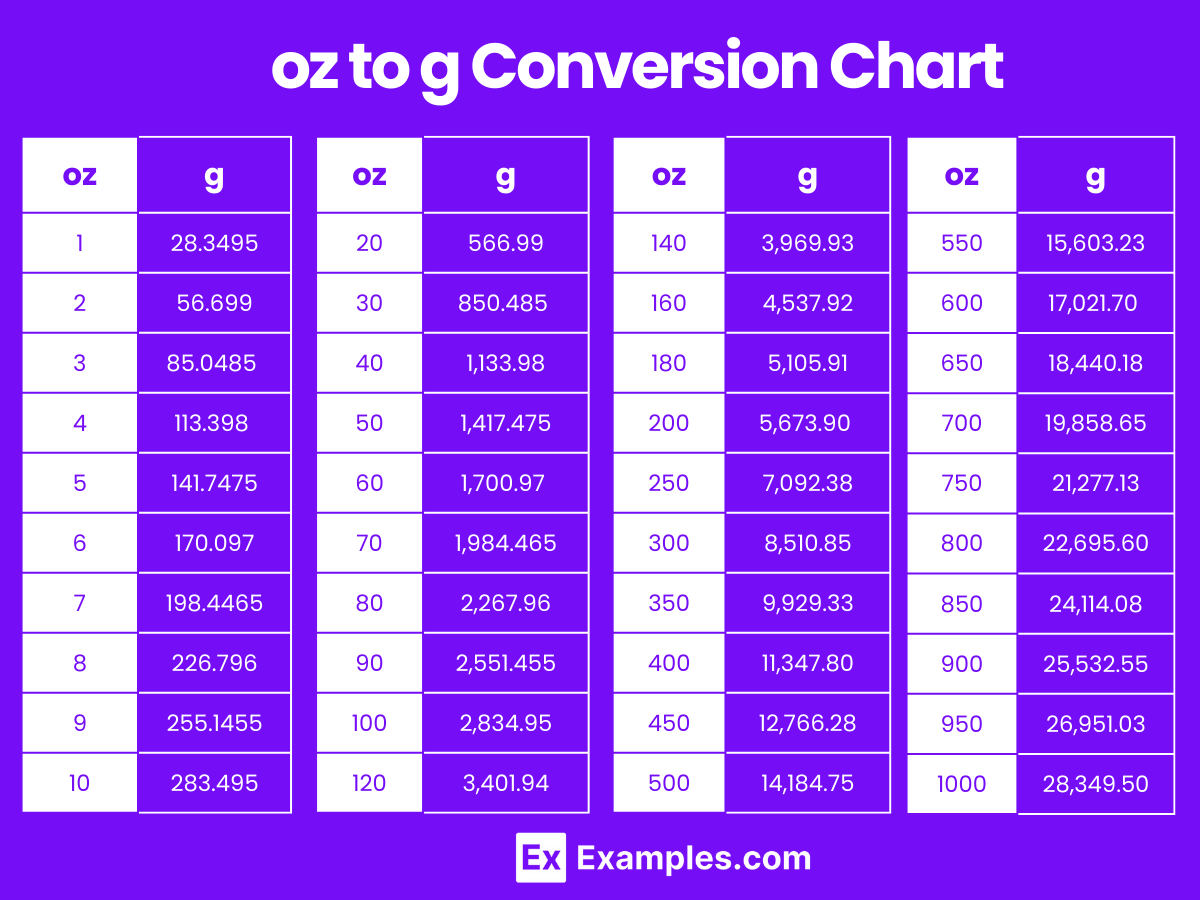
Ounces to Grams Conversion Table
| Ounces (oz) | Grams (g) |
|---|---|
| 1 oz | 28.3495 g |
| 2 oz | 56.699 g |
| 3 oz | 85.0485 g |
| 4 oz | 113.398 g |
| 5 oz | 141.7475 g |
| 6 oz | 170.097 g |
| 7 oz | 198.4465 g |
| 8 oz | 226.796 g |
| 9 oz | 255.1455 g |
| 10 oz | 283.495 g |
| 20 oz | 566.99 g |
| 30 oz | 850.485 g |
| 40 oz | 1,133.98 g |
| 50 oz | 1,417.475 g |
| 60 oz | 1,700.97 g |
| 70 oz | 1,984.465 g |
| 80 oz | 2,267.96 g |
| 90 oz | 2,551.455 g |
| 100 oz | 2,834.95 g |
oz to g Conversion Chart
Differences Between Grams to Ounces
| Aspect | Grams (g) | Ounces (oz) |
|---|---|---|
| Definition | A gram is a unit of mass in the metric system. | An ounce is a unit of mass in the US customary and British Imperial systems. |
| Symbol | g | oz |
| Conversion Factor | 1 gram = 0.03527396 ounces | 1 ounce = 28.3495 grams |
| Usage | Commonly used for measuring small quantities of mass. | Used for measuring both small and moderate quantities of mass, especially in cooking and food labeling. |
| Typical Context | Used in everyday contexts like cooking, medicine, and small-scale measurements. | Used in contexts like food recipes, food packaging, and mail weights. |
| Measurement Precision | Suitable for precise, small-scale measurements. | Suitable for both precise small-scale and moderate-scale measurements. |
| Scale | Smaller scale unit compared to ounces. | Larger scale unit compared to grams. |
| Practical Example | 200 grams of flour for a recipe. | 8 ounces of water in a glass. |
| Applications | Widely used in science, medicine, and daily life globally. | Commonly used in the US and UK for various weight measurements. |
| Common Equipment | Measured with kitchen scales, digital balances, and scientific equipment. | Measured with kitchen scales, grocery scales, and postal scales. |
| Historical Origin | Part of the metric system, established in France during the 1790s. | Part of the British Imperial system, historically used in trade and commerce. |
| International Use | Universally recognized and used globally. | Primarily used in the US, UK, and other countries that follow the Imperial system. |
1. Solved Examples on Converting Grams to Ounces
Example 1:
Problem: Convert 500 grams to ounces.
Ounces=Grams×0.03527396
Solution: 500×0.03527396=17.63698 oz
Example 2:
Problem: Convert 100 grams to ounces.
Solution: 100×0.03527396=3.527396 oz
Example 3:
Problem: Convert 250 grams to ounces.
Solution: 250×0.03527396=8.81849 oz
Example 4:
Problem: Convert 1,000 grams to ounces.
Solution: 1,000×0.03527396=35.27396 oz
Example 5:
Problem: Convert 50 grams to ounces.
Solution: 50×0.03527396=1.763698 oz
2. Solved Examples on Converting Ounces to Grams
Example 1:
Problem: Convert 5 ounces to grams.
Solution: Grams=Ounces×28.3495
Grams=5×28.3495=141.7475 g
Example 2:
Problem: Convert 10 ounces to grams.
Solution: Grams=10×28.3495=283.495 g
Example 3:
Problem: Convert 3 ounces to grams.
Solution: Grams=3×28.3495=85.0485 g
Example 4:
Problem: Convert 1 ounce to grams.
Solution: Grams=1×28.3495=28.3495 g
Example 5:
Problem: Convert 7 ounces to grams.
Solution: Grams=7×28.3495=198.4465 g
Why would I need to convert grams to ounces?
Converting grams to ounces is useful when you need to measure or understand weights in the context of cooking, nutrition, and postal services, where ounces are commonly used.
Are there any tools available to help convert grams to ounces?
Yes, you can use online conversion calculators, mobile apps, or scientific calculators to easily convert grams to ounces.
What are some practical uses for converting grams to ounces?
Practical uses include measuring ingredients for recipes, understanding nutrition labels, and weighing packages for shipping.
Is it possible to convert fractional grams to ounces?
Yes, fractional grams can be converted to ounces by multiplying the fractional value by 0.03527396.
Do industries use gram to ounce conversions frequently?
Certain industries, such as food production, pharmaceuticals, and postal services, often use these conversions for accurate weight measurements.

