Related rates problems are a critical aspect of AP Calculus, challenging students to apply derivatives to real-world situations. These problems involve finding the rate at which one quantity changes with respect to time based on the rate of change of another related quantity. By leveraging the chain rule and implicit differentiation, students can solve complex scenarios involving geometric shapes, motion, and fluid dynamics. Mastery of related rates not only tests calculus skills but also enhances problem-solving abilities, essential for success in both AP Calculus AB and BC exams.
Learning Objectives
When studying “Solving Related Rates Problems” for the AP Calculus AB and BC exam, you should focus on learning how to identify and relate different quantities that change over time, establish the correct equations linking these quantities, and apply differentiation, particularly the chain rule, to find the unknown rate of change. Additionally, practice interpreting the results in the context of real-world problems, ensuring accuracy in setting up equations, differentiating implicitly, and correctly substituting values to solve the problems efficiently during the exam.
Solving Related Rates Problems: A Comprehensive Guide for AP Calculus AB and BC
Related rates problems are crucial for both AP Calculus AB and BC exams. These problems involve determining the rate at which one quantity changes concerning time based on the rate of another related quantity. The ability to solve these problems is essential for understanding how calculus applies to real-world situations.
Key Concepts of Solving Related Rates Problems

- Understanding the Problem:
- Identify all quantities involved and their relationship.
- Determine which rates are given and which rate you need to find.
- Relationship Between Quantities:
- Formulate an equation relating the quantities, typically using geometric or physical principles.
- Differentiate with Respect to Time:
- Implicitly differentiate the equation with respect to time t, applying the chain rule.
- Substitute Known Values:
- Substitute the given values into the differentiated equation to solve for the unknown rate.
- Interpret the Answer:
- Ensure the units are correct and interpret the result in the context of the problem.
AP Calculus AB: Focus on Core Related Rates Problems

AP Calculus AB covers the fundamental concepts of related rates problems. The focus is on problems that involve basic geometric shapes and straightforward relationships.Step-by-Step Process for AP Calculus AB
- Identify Variables and Rates:
- Let x(t) and y(t) represent the changing quantities over time.
- For example, given dx/dt , find dy/dt.
- Establish the Relationship:
- Use a basic geometric formula. For example, with a ladder leaning against a wall: x2+y2 = L2
- Here, x is the distance from the wall, y is the height, and L is the ladder length.
- Differentiate with Respect to Time:
- Differentiate both sides using the chain rule:
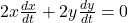
- Solve for dy/dt:
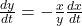
- Differentiate both sides using the chain rule:
- Substitute Known Values:
- Plug in the specific values of x, y, and dx/dt to find dy/dt.
- Interpret the Result:
- Determine the meaning of the sign and magnitude of the rate.
Common Related Rates Problems in AP Calculus AB
- Ladder Problems:
- Example: A 10 ft ladder is leaning against a wall, with the bottom pulled away at 1 ft/sec. How fast is the top sliding down when the bottom is 6 ft from the wall?
- Solution: Use the steps outlined above to find that the top of the ladder slides down at 43 ft/sec.
- Sphere Problems:
- Example: A balloon is inflated such that its radius increases at a constant rate. Find the rate at which the volume increases.
- Solution: Use the volume formula V = 4/3 πr3 and differentiate to find dV/dt.
AP Calculus BC: Advanced Related Rates Problems

AP Calculus BC includes all the topics from AB but also delves into more complex scenarios, including problems involving non-geometric relationships and additional calculus concepts like parametric equations and polar coordinates.Step-by-Step Process for AP Calculus BC
The steps for solving related rates problems in BC are similar to those in AB, but the problems can involve more intricate relationships.
- Identify Variables and Rates:
- In BC, problems might involve multiple related variables or require you to differentiate parametric equations.
- Establish the Relationship:
- For example, in a problem involving a conical tank, the relationship between height h, radius r, and volume V might involve more complex geometric principles: V = 1/3 πr2h
- In a polar coordinates problem, you might use r(θ) and differentiate with respect to θ.
- Differentiate with Respect to Time:
- Apply the chain rule as before but be prepared to handle more complex derivatives, such as implicit differentiation involving more than two variables.
- Substitute Known Values:
- Plug in values carefully, especially in parametric or polar problems where rates of change might not be directly given.
- Interpret the Result:
- Understand the physical or geometric meaning of the result, particularly when dealing with advanced contexts like polar coordinates.
Common Related Rates Problems in AP Calculus BC
- Conical Tank Problems:
- Example: Water flows into a conical tank, and you need to find the rate at which the water level rises.
- Solution: Differentiate the volume equation with respect to time, using the relationship between h and r specific to the cone’s dimensions.
- Parametric or Polar Coordinate Problems:
- Example: A particle moves along a path defined by parametric equations, and you need to find the rate of change of one coordinate with respect to another.
- Solution: Differentiate the parametric equations with respect to time and find the required rate.
Examples
Example 1: Ladder Sliding Down a Wall
A 10-foot ladder is leaning against a wall. If the bottom of the ladder is pulled away from the wall at 2 feet per second, how fast is the top of the ladder sliding down the wall when the bottom is 6 feet from the wall? This problem involves applying the Pythagorean theorem to relate the height of the ladder on the wall and the distance of the bottom from the wall.
Example 2: Expanding Circle
A circle’s radius is increasing at a rate of 3 inches per second. How fast is the area of the circle increasing when the radius is 5 inches? Here, you’ll use the area formula for a circle and differentiate with respect to time to find the rate of change of the area as the radius expands.
Example 3: Filling a Conical Tank
Water is being poured into a conical tank at a rate of 10 cubic feet per minute. If the tank has a height of 12 feet and a radius of 4 feet, how fast is the water level rising when the water is 3 feet deep? This problem requires you to relate the volume of the water to its height using the geometry of the cone and then differentiate with respect to time.
Example 4: Shadow Lengthening
A 6-foot-tall person walks away from a 15-foot streetlight at a rate of 4 feet per second. How fast is the tip of the person’s shadow moving when the person is 10 feet away from the streetlight? This scenario involves similar triangles to relate the height of the person, the length of the shadow, and the distance from the streetlight.
Example 5: Balloon Inflating
A spherical balloon is being inflated, and its volume is increasing at a rate of 100 cubic centimeters per second. How fast is the radius of the balloon increasing when the radius is 10 centimeters? In this example, you’ll use the volume formula for a sphere and differentiate to find the rate of change of the radius as the balloon expands.
Multiple Choice Questions
Question 1
A 10-foot ladder is leaning against a wall. The bottom of the ladder is being pulled away from the wall at 1 foot per second. How fast is the top of the ladder sliding down the wall when the bottom is 6 feet away from the wall?
A) 0.5 ft/sec
B) 0.6 ft/sec
C) 0.75 ft/sec
D) 0.8 ft/sec
Answer: C) 0.75 ft/sec
Explanation:
- Step 1: Use the Pythagorean theorem to relate the height y of the ladder on the wall and the distance x of the bottom from the wall: x2+y2 = 102 = 100
- Step 2: Differentiate both sides with respect to time t:
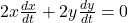
- Simplify to:
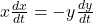
- Step 3: When x=6 feet, solve for y:
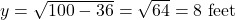
- Step 4: Substitute x = 6, y = 8, and dx/dt = 1 ft/sec into the equation: 6(1)=−8 dy/dt dy/dt = −6/8 = −0.75 ft/sec
- The magnitude is 0.75 ft/sec. Therefore, the correct answer is
- C) 0.75 ft/sec.
Question 2
A balloon is being inflated and the radius of the balloon is increasing at a rate of 0.5 inches per second. What is the rate of change of the volume of the balloon when the radius is 3 inches? (Use V=4/3 πr3 for the volume of a sphere.)
A) 6π cubic inches per second
B) 9π cubic inches per second
C) 18π cubic inches per second
D) 27π cubic inches per second
Answer: C) 18π cubic inches per second
Explanation:
- Step 1: Differentiate the volume formula with respect to time t:
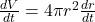
- Step 2: Substitute r=3 inches and dtdr=0.5 inches per second: dV/dt = 4π(3)2(0.5)= 4π(9)(0.5) = 18π cubic inches per second
- Therefore, the correct answer is
- C) 18π cubic inches per second.
Question 3
A circular ripple spreads out in a pond, with the radius of the circle increasing at a constant rate of 2 inches per second. How fast is the area of the circle increasing when the radius is 5 inches? (Use A = πr2 for the area of a circle.)
A) 10π square inches per second
B) 15π square inches per second
C) 20π square inches per second
D) 25π square inches per second
Answer: C) 20π square inches per second
Explanation:
- Step 1: Differentiate the area formula with respect to time t:
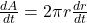
- Step 2: Substitute r=5 inches and dtdr=2 inches per second: dA/dt = 2π(5)(2)=20π square inches per second
- Therefore, the correct answer is
- C) 20π square inches per second.


