Using Definite Integrals to Determine Accumulated Change Over an Interval

Last Updated: September 23, 2024

Notes

In both AP Calculus AB and BC, understanding how to use definite integrals to determine accumulated change over an interval is essential. This concept involves calculating the total change in a quantity when its rate of change is known over a specific interval. By integrating a rate function, such as velocity or growth rate, over a given interval, you can determine the net accumulation, whether it’s displacement, total growth, or other quantities. Mastery of this topic is key to solving many real-world problems in calculus.

Free AP Calculus AB Practice Test

Free AP Calculus BC Practice Test

Learning Objectives

By studying “Using Definite Integrals to Determine Accumulated Change Over an Interval” for the AP Calculus AB and BC exams, you should learn to interpret and calculate the accumulated change of a quantity using definite integrals. Understand how to apply the Fundamental Theorem of Calculus to evaluate integrals, and use integrals to solve real-world problems involving rates of change, such as displacement, area, and total accumulation. Master the application of these concepts to both straightforward and advanced scenarios in parametric, polar, and series contexts (BC).

Understanding Accumulated Change

Accumulated change refers to the total amount of change in a quantity over a specific interval. If you know the rate at which a quantity changes, you can use a definite integral to find the total change over an interval.Rate of Change and Accumulation

If f(x) represents a rate of change of some quantity at any point x, then the accumulated change of that quantity from x = a to x = b can be determined by the definite integral:

$\text{Accumulated Change} = \int_{a}^{b} f(x) \, dx$

Here:

f(x) is the rate of change function.
[a,b] is the interval over which you’re measuring the change.
The integral $\int_{a}^{b} f(x) \, dx$ calculates the net accumulation of the quantity over the interval from x = a to x = b.

Physical Interpretation

The integral $\int_{a}^{b} f(x) \, dx$ can be understood as the area under the curve of f(x) between x = a and x = b. This area represents the total accumulated change in the quantity you’re measuring.

Example: Velocity and Displacement

Suppose v(t) represents the velocity of an object at time t. The displacement (or change in position) of the object from time t = a to t = b can be found by: $\text{Displacement} = \int_{a}^{b} v(t) \, dt$

If v(t) is positive, the object is moving forward, and if v(t) is negative, the object is moving backward. The definite integral accounts for these directions, providing the net displacement.

Example: Growth Rate and Population

If r(t) represents the rate of growth of a population at time t, then the total increase in population from t = a to t = b is given by: $\text{Total Population Increase} = \int_{a}^{b} r(t) \, dt$

This integral calculates the total number of individuals added to the population over the interval.

AP Calculus AB and AP Calculus BC

AP Calculus AB

In AP Calculus AB, you will focus on understanding how definite integrals calculate accumulated change in contexts such as:

Displacement from velocity.
Area under a curve.
Total amount of a substance added or removed over time.

Key Concepts:

Fundamental Theorem of Calculus (Part 1): Connects the definite integral to the antiderivative. $\int_{a}^{b} f(x) \, dx = F(b) - F(a)$
Where F(x) is an antiderivative of f(x).
Applications: Finding the area under a curve, total distance traveled, and net change in quantities.

AP Calculus BC

AP Calculus BC expands on these ideas with additional topics, such as:

Improper Integrals: Integrals with infinite limits or integrands with discontinuities.
Parametric Equations and Polar Coordinates: Integrals that calculate accumulated change when the curve is defined parametrically or in polar form.
Series and Sequences: Accumulation in terms of infinite series.

Additional Topics:

Arc Length and Surface Area: Integrals used to calculate the length of a curve and the surface area of a solid of revolution. Example for Arc Length: $\text{Arc Length} = \int_{a}^{b} \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \, dx$
Advanced Applications: Such as work done by a force, center of mass, and fluid force.

Step-by-Step Process

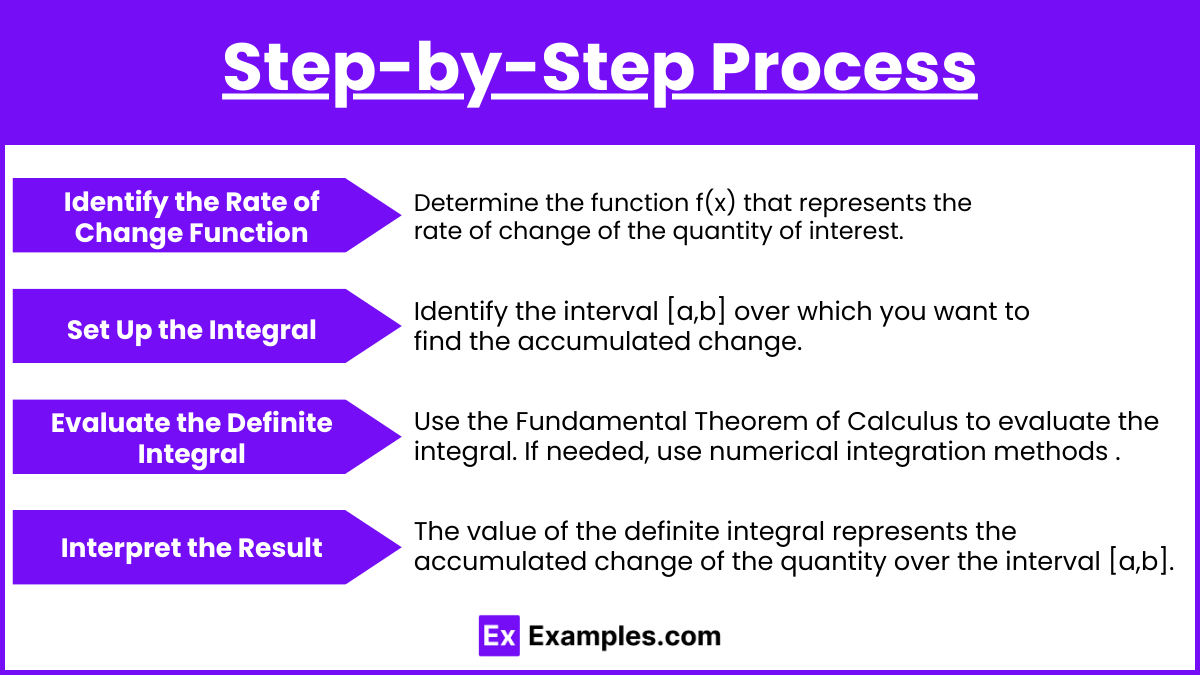
1. Identify the Rate of Change Function

Determine the function f(x) that represents the rate of change of the quantity of interest. This could be a velocity function representing the rate of change of position, a growth rate in a population model, or any other context where change is occurring continuously.

2. Set Up the Integral

Identify the interval [a,b] over which you want to find the accumulated change. $\int_{a}^{b} f(x) \, dx$ . This interval should correspond to the period over which the change is being measured.

3. Evaluate the Definite Integral

Use the Fundamental Theorem of Calculus to evaluate the integral. If needed, use numerical integration methods for complex functions. If the function is complex or lacks a simple antiderivative, use numerical integration methods such as Riemann sums, Trapezoidal Rule, or Simpson’s Rule to approximate the integral.

4. Interpret the Result

The value of the definite integral represents the accumulated change of the quantity over the interval [a,b]. Make sure to relate the mathematical result back to the real-world scenario, ensuring that the units and the interpretation make sense in the given context.

Examples

Example 1: Accumulating Distance from Velocity

Suppose a car’s velocity over time is given by the function v(t) = 3t²+2t (in meters per second) for t in seconds. To find the total distance the car travels between t = 1 second and t = 4 seconds, you would integrate the velocity function over that interval:

$\text{Distance} = \int_{1}^{4} v(t) \, dt = \int_{1}^{4} (3t^2 + 2t) \, dt$

Evaluating this integral provides the accumulated distance traveled by the car over the 3-second interval.

Example 2: Calculating Net Displacement from Velocity

Consider a particle moving along a line with its velocity given by v(t) = sin(t)−cos(t) meters per second. To determine the net displacement of the particle from t = 0 to t = 2π, you compute the definite integral:

$\text{Net Displacement} = \int_{0}^{2\pi} (\sin(t) - \cos(t)) \, dt$

This integral provides the accumulated change in the particle’s position, accounting for both forward and backward motion.

Example 3 : Accumulating Area Under a Curve

The revenue generated by a company over time can be modeled by the function R(t) = 100e^0.05t dollars per day. To find the total revenue generated from day 0 to day 10, you integrate the revenue function over this interval:

$\text{Total Revenue} = \int_{0}^{10} 100e^{0.05t} \, dt$

The result of this integral represents the accumulated revenue over the 10-day period.

Example 4: Accumulating Heat from a Rate of Temperature Change

Suppose the rate at which a substance’s temperature changes over time is given by $\frac{dT}{dt} = 5t - 2$ degrees per minute. To find the total change in temperature from t = 0 minutes to t = 6 minutes, you integrate the rate of change of temperature:

$\text{Total Temperature Change} = \int_{0}^{6} (5t - 2) \, dt$

This integral calculates the accumulated change in temperature over the 6-minute interval.

Example 5: Accumulating Population Growth

A population of bacteria grows according to the rate $\frac{dP}{dt} = 300e^{0.02t}$ bacteria per hour. To determine the total increase in the population over the first 5 hours, you would integrate this rate of growth:

$\text{Total Population Increase} = \int_{0}^{5} 300e^{0.02t} \, dt$

The definite integral gives the accumulated change in the population, reflecting the total number of bacteria added over the 5-hour period.

Multiple Choice Questions

Question 1

A car’s velocity is given by v(t) = 5t²−3t meters per second. What is the total distance the car travels from t = 1 second to t = 3 seconds?

A) 16 meters
B) 28 meters
C) 50 meters
D) 64 meters

Answer: C) 50 meters

Explanation: To find the total distance, we calculate the integral of the velocity function from t = 1 to t = 3:

$\text{Distance} = \int_{1}^{3} (5t^2 - 3t) \, dt$

This integral tells us the total area under the curve of the velocity function, which represents the distance traveled. After computing, we find the distance to be 50 meters.

Question 2

Water flows into a tank at a rate given by R(t) = 2+4t liters per minute. How much water enters the tank from t = 0 to t = 5 minutes?

A) 30 liters
B) 45 liters
C) 70 liters
D) 90 liters

Answer: C) 70 liters

Explanation: To find out how much water has entered the tank, we calculate the integral of the rate function from t = 0 to t = 5:

$\text{Total Water} = \int_{0}^{5} (2 + 4t) \, dt$

This integral gives us the total water accumulated over 5 minutes, which is 70 liters.

Question 3

A particle moves with a velocity given by v(t) = 3sin(t) meters per second. What is the net displacement of the particle from t = 0 to t = π seconds?

A) 0 meters
B) 3 meters
C) 6 meters
D) 9 meters

Answer: A) 0 meters

Explanation: The net displacement is the total change in position. We calculate this by integrating the velocity function from t = 0 to t = π:

$\text{Net Displacement} = \int_{0}^{\pi} 3\sin(t) \, dt$

Since sin(t) is positive for half the interval and negative for the other half, the total displacement ends up being 0 meters, meaning the particle returns to its starting point.