Resources

Calculating Equilibrium Concentrations

Team English - Examples.com
Last Updated: September 24, 2024

Learning Objectives

By studying the topic of Calculating Equilibrium Concentrations for the AP Chemistry exam, you should be able to understand the concept of chemical equilibrium and the significance of the equilibrium constant (K꜀​ and Kₚ). You should learn how to write and interpret equilibrium expressions, use initial concentrations to set up and solve for equilibrium concentrations using the ICE table method, and apply stoichiometric relationships to determine changes in concentration. Additionally, you should be able to solve quadratic equations when necessary, make valid approximations to simplify calculations, and understand how changes in conditions (such as concentration, temperature, and pressure) affect the equilibrium position.

Free AP Chemistry Practice Test

Introduction

Calculating equilibrium concentrations involves determining the concentrations of reactants and products in a chemical reaction at equilibrium. At this point, the rate of the forward reaction equals the rate of the reverse reaction, leading to constant concentrations of all species involved. This process typically requires the use of the equilibrium constant (Keq), which is derived from the balanced chemical equation and provides a ratio of product concentrations to reactant concentrations. By applying the principles of stoichiometry and the initial concentrations of the reactants, we can solve for the equilibrium concentrations, providing insights into the reaction’s behavior under specific conditions.

What is Chemical Equilibrium?

Chemical equilibrium is a state in a chemical reaction where the rates of the forward and reverse reactions are equal, resulting in the concentrations of the reactants and products remaining constant over time. At equilibrium, there is no net change in the amounts of reactants and products, although the reactions continue to occur. This dynamic balance can be represented by the equation:

aA + bB ⇌ cC + dD

In this state, the system’s macroscopic properties, such as concentration, pressure, and color, remain unchanged.

What are Equilibrium Concentrations?

What are Equilibrium Concentrations?

Equilibrium concentrations are the concentrations of reactants and products in a chemical reaction mixture when the reaction has reached chemical equilibrium. At this point, the concentrations remain constant over time because the rates of the forward and reverse reactions are equal. These concentrations can be used to calculate the equilibrium constant, which quantifies the ratio of product concentrations to reactant concentrations in a balanced chemical equation.

The Equilibrium Constant (K)

The Equilibrium Constant (K) is a numerical value that represents the ratio of the concentrations of products to reactants at equilibrium for a reversible chemical reaction. It is specific to a particular reaction at a given temperature. The value of K indicates the extent to which a reaction proceeds: a large K (K >> 1) means the reaction favors products, while a small K (K << 1) means it favors reactants. The equilibrium constant expression is derived from the balanced chemical equation and involves raising the concentration of each species to the power of its coefficient in the equation.

Expression for K꜀

K꜀ = \frac{[C]^c [D]^d}{[A]^a [B]^b}

Where:

  • [A], [B], [C], [D] are the molar concentrations of the reactants and products.
  • a, b, c, d are the coefficients from the balanced chemical equation.

Expression for Kₚ​

Kₚ = \frac{(P_C)^c (P_D)^d}{(P_A)^a (P_B)^b}

Where:

  • PA​, PB, PC​, PD​ are the partial pressures of the gaseous reactants and products.
  • a, b, c, d are the coefficients from the balanced chemical equation.

Steps to Calculate Equilibrium Concentrations

Steps to Calculate Equilibrium Concentrations

Step 1: Write the Balanced Chemical Equation

Ensure you have a balanced chemical equation for the reaction. This step is crucial as the coefficients will be used in subsequent calculations.

Step 2: Write the equilibrium expression (K꜀ or Kₚ​).

Based on the balanced equation, write the equilibrium expression for K꜀(if using concentrations) or Kₚ​ (if using partial pressures). For a general reaction: aA + bB ⇌ cC + dD

The expressions are:

K꜀ = \frac{[C]^c [D]^d}{[A]^a [B]^b}

Kₚ = \frac{(P_C)^c (P_D)^d}{(P_A)^a (P_B)^b}

Step 3: List initial concentrations (or partial pressures).

Determine the initial concentrations or partial pressures of all reactants and products. This information is usually provided in the problem statement.

Step 4: Define changes in concentrations using stoichiometry (often done with an ICE table).

Set up an ICE (Initial, Change, Equilibrium) table to track changes in concentrations (or partial pressures) as the system moves towards equilibrium. Define the changes in terms of a variable x, which represents the change in concentration.

ICE Table Setup

For the reaction:

aA + bB ⇌ cC + dD

The ICE table looks like this:

Initial (M)Change (M)Equilibrium (M)
[A][A]₀-ax[A]₀ – ax
[B][B]₀-bx[B]₀ – bx
[C][C]₀+cx[C]₀ + cx
[D][D]₀+dx[D]₀ + dx

Step 5: Write the Expression for Equilibrium Concentrations

Using the ICE table, write the expressions for the equilibrium concentrations of all species in terms of the initial concentrations and the variable x.

Step 6: Substitute Equilibrium Concentrations into the Equilibrium Expression

Substitute the expressions from the ICE table into the equilibrium expression K꜀ or Kₚ​.

Step 7: Solve for the Unknown(s)

Solve the resulting equation for x. This step might involve solving a quadratic equation or making approximations if x is small compared to the initial concentrations.

Practice Problems

Problem 1: For the reaction:

H₂(g) + I₂(g) ⇌ 2HI(g)

At a certain temperature, K꜀ = 50.0. Initially, 1.00 M H2​ and 1.00 M I2​ are mixed.

Find the equilibrium concentrations of all species.

Solution:

  1. Write the balanced chemical equation: H₂(g) + I₂(g) ⇌ 2HI(g)
  2. Write the equilibrium expression: K_c = \frac{[\text{HI}]^2}{[\text{H}_2][\text{I}_2]}
  3. List initial concentrations:
Initial (M)
H₂1.00
I₂1.00
HI0.00
  1. Define changes in concentrations using stoichiometry (ICE Table):

Here is the corrected table format:

Initial (M)Change (M)Equilibrium (M)
H₂1.00-x1.00 – x
I₂1.00-x1.00 – x
HI0.00+2x2x
  1. Substitute equilibrium concentrations into the equilibrium expression
    • K_c = \frac{(2x)^2}{(1.00 - x)(1.00 - x)}= 50.0
    • \frac{4x^2} {(1.00 - x)^2}= 50.0
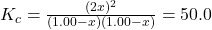
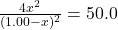
    • 4x² = 50.0(1.00 – x)²
    • 4x² = 50.0(1.00 – 2x + x²)
    • 4x² = 50.0 – 100x + 50.0x²
    • 0 = 50.0x² – 4x² – 100x + 50.0
    • 0 = 46x² – 100x + 50.0
    • 46x² – 100x + 50.0 = 0
  1. Solve the quadratic equation:
    • Using the quadratic formula ( ax² + bx + c = 0 ),
    • where ( a = 46 ), ( b = -100 ), and ( c = 50.0 ):
    • x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
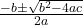
    • Substitute the values
    • x = \frac{100 \pm \sqrt{(-100)^2 - 4(46)(50.0)}}{2(46)}
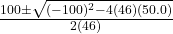
    • x = \frac{100 \pm \sqrt{10000 - 9200}}{92}
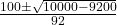
    • x = \frac{100 \pm \sqrt{800}}{92}
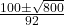
    • x = \frac{100 \pm 28.28}{92}
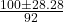
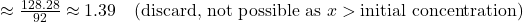
    • x \approx \frac{128.28}{92} \approx 1.39 \quad (\text{discard, not possible as } x > \text{initial concentration})
    • x \approx \frac{71.72}{92} \approx 0.78
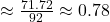
  1. Calculate equilibrium concentrations:
Equilibrium (M)
H₂1.00 – 0.78 = 0.22
I₂1.00 – 0.78 = 0.22
HI2(0.78) = 1.56

Problem 2: For the reaction:

N₂O₄(g) ⇌ 2NO₂(g)

At a certain temperature, K꜀ = 0.36. Initially, 0.50 M N₂O₄​ is present with no NO₂​.

Find the equilibrium concentrations of all species.

  1. Write the balanced chemical equation: N₂O₄(g) ⇌ 2NO₂(g)
  2. Write the equilibrium expression: K_c = \frac{[\text{NO}_2]^2}{[\text{N}_2O_4]}
  3. List initial concentrations:
Initial (M)
N₂O₄0.50
NO₂0.00
  1. Define changes in concentrations using stoichiometry (ICE Table):
Initial (M)Change (M)Equilibrium (M)
N₂O₄0.50-x0.50 – x
NO₂0.00+2x2x
  1. Substitute equilibrium concentrations into the equilibrium expression:
    • K_c = \frac{(2x)^2}{0.50 - x}= 0.36
    • \frac{4x^2}{0.50 - x} = 0.36
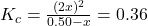
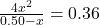
    • 4x² = 0.36(0.50 – x)
    • 4x² = 0.18 – 0.36x
    • 4x² + 0.36x – 0.18 = 0
  1. Solve the quadratic equation:
    • Given the quadratic equation ( ax² + bx + c = 0 ),
    • where ( a = 4 ), ( b = 0.36 ), and ( c = -0.18 ):
    • x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
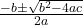
    • Substitute the values:
    • x = \frac{-0.36 \pm \sqrt{(0.36)^2 - 4(4)(-0.18)}}{2(4)}
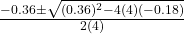
    • x = \frac{-0.36 \pm \sqrt{0.1296 + 2.88}}{8}
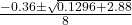
    • x = \frac{-0.36 \pm \sqrt{3.0096}}{8}
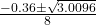
    • x = \frac{-0.36 \pm 1.734}{8}
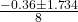
    • x \approx \frac{1.374}{8} \approx 0.17 \quad (\text{discard negative value as } x \text{ cannot be negative})
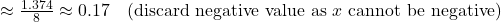
  1. Calculate equilibrium concentrations:
SpeciesEquilibrium (M)
N₂O₄0.50 – 0.17 = 0.33
NO₂2(0.17) = 0.34