Collision Model
Learning Objectives
For the AP Chemistry exam, mastering the Collision Model involves understanding the conditions required for effective collisions, including the concepts of collision frequency, activation energy, and proper molecular orientation. You should learn how various factors such as concentration, temperature, surface area, and catalysts influence reaction rates and be able to explain these effects using the Collision Model. Additionally, familiarity with the Maxwell-Boltzmann distribution and the Arrhenius Equation will help in quantitatively analyzing reaction rates.
Introduction
The Collision Model is a key concept in chemical kinetics that explains how chemical reactions occur and why their rates vary. According to this model, for a reaction to take place, reactant molecules must collide with sufficient energy and in the correct orientation. This theory highlights three essential factors influencing reaction rates: collision frequency, activation energy, and proper molecular orientation. By understanding and manipulating these factors, chemists can predict and control the speed of chemical reactions, making the Collision Model a fundamental tool in both theoretical and applied chemistry.
What is Collision Model?
The Collision Model is a theory in chemistry that states for a chemical reaction to occur, reactant molecules must collide with sufficient energy and proper orientation. This model explains how reaction rates depend on the frequency of collisions, the energy of collisions (activation energy), and the orientation of the colliding molecules.
Essential Requirements for a Reaction
1. Collision Frequency
Definition: Collision frequency refers to the number of times reactant molecules collide per unit of time.
- Impact on Reaction Rate: A higher collision frequency increases the chances of reactant molecules interacting and forming products. More collisions mean more opportunities for the reactants to meet and potentially react.
- Factors Influencing Collision Frequency:
- Concentration: Higher concentrations of reactants lead to more collisions because there are more molecules present in a given volume.
- Pressure: For gases, increasing the pressure reduces the volume, bringing molecules closer together and increasing collision frequency.
- Temperature: Higher temperatures increase the kinetic energy of molecules, causing them to move faster and collide more often.
2. Activation Energy (Ea)
Definition: Activation energy is the minimum amount of energy that reactant molecules must possess for a collision to result in a chemical reaction.
- Energy Barrier: Activation energy represents the energy barrier that must be overcome for reactants to be transformed into products. This barrier is due to the energy needed to break bonds in the reactants and form new bonds in the products.
- Role in Reaction Rate: Only collisions with energy equal to or greater than the activation energy will lead to a reaction. The higher the activation energy, the fewer the number of successful collisions, and thus, the slower the reaction rate.
- Effect of Temperature: Increasing the temperature increases the kinetic energy of the molecules, leading to more collisions with sufficient energy to overcome the activation energy barrier.
3. Proper Orientation
Definition: Proper orientation means that reactant molecules must collide in a specific way that allows the formation of new bonds and the conversion of reactants to products.
- Steric Factor: The orientation requirement is often described by the steric factor, which is a measure of the fraction of collisions that have the correct orientation for a reaction to occur.
- Importance of Orientation: Even if collisions occur with sufficient energy, incorrect orientation can prevent the formation of the transition state necessary for the reaction to proceed. For example, in the reaction between two diatomic molecules, the specific atoms that need to react must collide directly.
- Influence of Molecular Structure: The structure and geometry of molecules play a significant role in determining the likelihood of proper orientation during collisions.
Maxwell-Boltzmann Distribution
The Maxwell-Boltzmann Distribution describes the distribution of kinetic energies among molecules in a gas.
Understanding the Distribution
- Distribution Curve: The Maxwell-Boltzmann distribution is typically represented by a curve that shows the number of molecules (y-axis) versus their kinetic energy (x-axis).
- Shape of the Curve: At lower temperatures, the curve is higher and narrower, indicating that most molecules have similar, relatively low energies. At higher temperatures, the curve flattens and spreads out, showing a wider range of kinetic energies with more molecules possessing higher energies.
Key Features
- Most Probable Energy: This is the energy corresponding to the peak of the curve, where the largest number of molecules is found.
- Average Energy: The mean energy of all the molecules in the distribution.
- High-Energy Tail: At the right end of the curve, the tail represents molecules with very high kinetic energy. The number of these high-energy molecules increases with temperature.
Implications for Reaction Rates
- Temperature and Reaction Rate: As temperature increases, the distribution shifts so that a greater proportion of molecules have higher kinetic energies. This means more molecules have enough energy to overcome the activation energy barrier, leading to an increased reaction rate.
- Activation Energy (Ea): Only a certain fraction of molecules in the distribution have kinetic energy equal to or greater than the activation energy. This fraction can be found by the area under the curve to the right of the activation energy threshold.
Mathematical Representation
The probability P(E) of a molecule having energy E in an ideal gas is given by the Maxwell-Boltzmann distribution formula:
\(\text{P(E)} = \left( \frac{2}{\sqrt{\pi}} \right) \left( \frac{1}{(k_BT)^{3/2}} \right) E^{1/2} \exp\left( -\frac{E}{k_BT} \right)\)
Where:
- E = Kinetic energy of the molecules
- k = Boltzmann constant
- T = Absolute temperature
Collision Theory and Arrhenius Equation
Collision Theory
Collision Theory explains how chemical reactions occur and why reaction rates differ among different reactions. According to this theory, for a reaction to take place, the reactant molecules must collide with sufficient energy and proper orientation.
Key Points of Collision Theory
- Collision Frequency: The number of collisions that occur per unit time in a system.
- Activation Energy (Eₐ): The minimum energy required for a collision to result in a reaction.
- Proper Orientation: Reactant molecules must be oriented in a specific way to allow the formation of new chemical bonds.
Factors Affecting Collision Theory
- Concentration: Higher concentrations lead to more frequent collisions.
- Temperature: Higher temperatures increase the kinetic energy of molecules, leading to more collisions with sufficient energy.
- Surface Area: Increased surface area allows more collisions to occur.
- Catalysts: Catalysts lower the activation energy, increasing the number of successful collisions.
Arrhenius Equation
The Arrhenius Equation quantitatively describes the effect of temperature on the reaction rate. It shows how the rate constant (k) changes with temperature and activation energy.
The Arrhenius Equation
\(\text{k} = \text {A} e^{-\frac{E_a}{RT}}\)
Where:
- k = Rate constant
- A = Frequency factor (also known as the pre-exponential factor), which accounts for the frequency of collisions and the probability of proper orientation
- Eₐ = Activation energy
- R = Universal gas constant (8.314 J/mol.K)
- T = Temperature in Kelvin
Components of the Arrhenius Equation
- Frequency Factor (A): Reflects how often molecules collide with the correct orientation.
- Exponential Factor 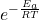\(e^{-\frac{E_a}{RT}}\): Represents the fraction of collisions that have enough energy to overcome the activation energy barrier.
Impact of Temperature on Reaction Rates
- Higher Temperature: Increases the kinetic energy of molecules, leading to more collisions with energy greater than or equal to the activation energy, thus increasing the reaction rate.
- Lower Temperature: Decreases the kinetic energy, resulting in fewer successful collisions and a slower reaction rate.
Examples
Decomposition of Hydrogen Peroxide
Reaction: 2H₂O₂ → 2H₂O + O₂
- Collision Frequency: Hydrogen peroxide molecules must frequently collide to decompose into water and oxygen.
- Activation Energy: The reaction requires sufficient energy to break the H₂O₂ bonds.
- Proper Orientation: The molecules must collide in a way that allows the O-O bond to break and form new H-O bonds.
- Catalyst: Adding manganese dioxide (MnO₂) lowers the activation energy, increasing the rate of decomposition by ensuring more effective collisions.
Combustion of Methane
Reaction: CH₄ + 2O₂ → CO₂ + 2H₂O
- Collision Frequency: Methane and oxygen molecules need to collide frequently for combustion to occur.
- Activation Energy: The reaction requires sufficient energy to break the C−H and O=O bonds.
- Proper Orientation: The methane and oxygen molecules must collide in a way that facilitates the breaking of bonds and the formation of new C=O and O−H bonds.
- Temperature: Increasing temperature raises the kinetic energy of the molecules, resulting in more frequent and energetic collisions that overcome the activation energy barrier.