Energy of Phase Changes

Last Updated: September 24, 2024

Notes

Learning Objectives

Understanding the energy involved in phase changes is crucial for the AP Chemistry exam. You should be able to identify and describe the six main types of phase changes (melting, freezing, vaporization, condensation, sublimation, deposition) and their endothermic or exothermic nature. Mastery involves calculating energy changes using specific heat, heat of fusion, and heat of vaporization. You need to interpret heating and cooling curves and apply these concepts to real-world scenarios. Solving complex problems that involve multiple phase changes is essential.

Free AP Chemistry Practice Test

Introduction

The energy of phase changes refers to the amount of energy required to transform a substance from one state of matter to another, such as from solid to liquid or liquid to gas. These transformations, known as phase transitions, involve either the absorption or release of heat energy without altering the substance’s temperature. Key phase changes include melting, freezing, vaporization, condensation, sublimation, and deposition, each of which is characterized by specific enthalpy changes. Understanding the energy dynamics of phase changes is crucial in fields like thermodynamics, material science, and chemistry, as it explains the behavior of substances under various thermal conditions.

Phases of Matter

Matter can exist in three primary phases: solid, liquid, and gas. Each phase has distinct physical properties determined by the arrangement and energy of its particles.

Solid Phase

Characteristics

Definite Shape and Volume: Solids maintain a fixed shape and volume.
Incompressible: Solids cannot be easily compressed due to tightly packed particles.
High Density: Particles are closely packed together, resulting in a high density.

Particle Arrangement

Structure: Particles in a solid are arranged in a fixed, orderly structure, often forming a crystalline lattice.
Movement: Particles vibrate in place but do not move freely.

Energy

Kinetic Energy: Solids have the lowest kinetic energy among the three phases.
Intermolecular Forces: Strong intermolecular forces hold particles together tightly.

Liquid Phase

Characteristics

Definite Volume, Indefinite Shape: Liquids take the shape of their container but have a fixed volume.
Slightly Compressible: Liquids are only slightly compressible because particles are close together.
Moderate Density: Liquids have a lower density than solids but higher than gases.

Particle Arrangement

Structure: Particles in a liquid are close together but not in a fixed position.
Movement: Particles can move past each other, allowing liquids to flow.

Energy

Kinetic Energy: Liquids have higher kinetic energy than solids.
Intermolecular Forces: Moderate intermolecular forces allow particles to move while remaining in close contact.

Gas Phase

Characteristics

Indefinite Shape and Volume: Gases take the shape and volume of their container.
Highly Compressible: Gases can be easily compressed due to large spaces between particles.
Low Density: Particles are far apart, resulting in low density.

Particle Arrangement

Structure: Particles in a gas are spread out and not arranged in any specific structure.
Movement: Particles move freely and rapidly in all directions.

Energy

Kinetic Energy: Gases have the highest kinetic energy among the three phases.
Intermolecular Forces: Weak intermolecular forces allow particles to move independently.

Phase Changes and Energy

Phase changes involve the transition of a substance from one state of matter to another. These transitions require or release energy, affecting the movement and arrangement of particles. Here, we will explore the different phase changes, the energy involved, and their characteristics.

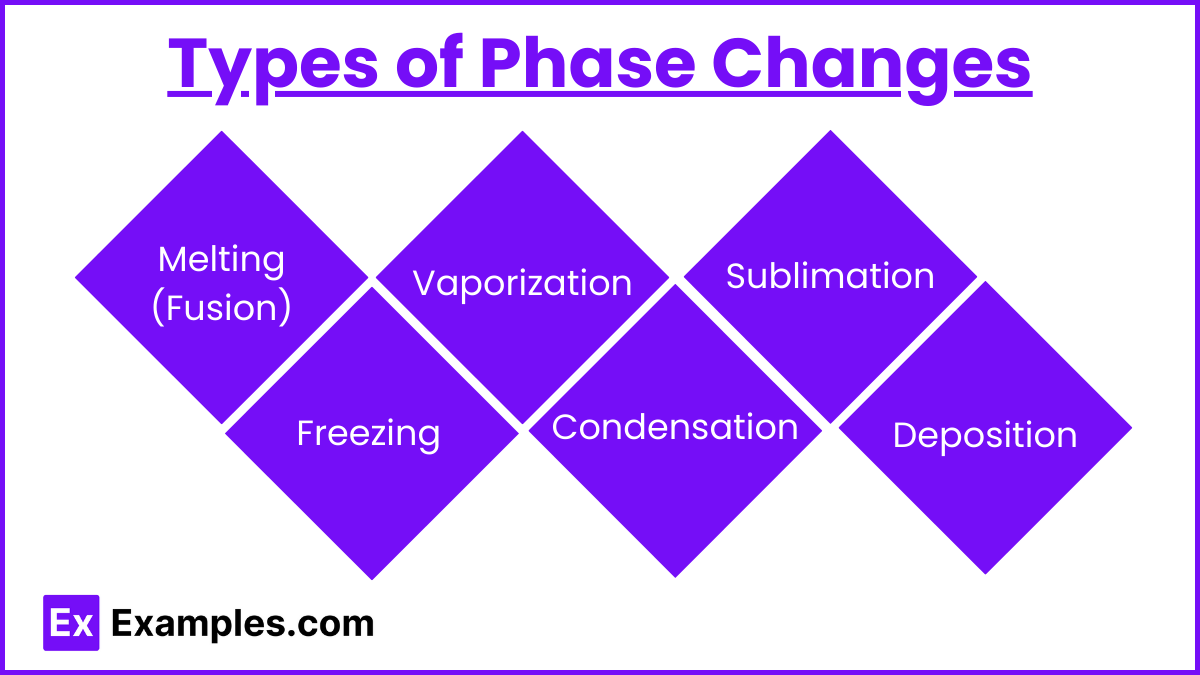
Types of Phase Changes

1. Melting (Fusion)

Process: Solid to liquid.
Energy Change: Absorbs heat (endothermic).
Key Term: Heat of fusion (ΔHբᵤₛ).
Equation: q = mΔHբᵤₛ

2. Freezing

Process: Liquid to solid.
Energy Change: Releases heat (exothermic).
Key Term: Heat of fusion (ΔHբᵤₛ), but negative.
Equation: q = −mΔHբᵤₛ

3. Vaporization (Boiling/Evaporation)

Process: Liquid to gas.
Energy Change: Absorbs heat (endothermic).
Key Term: Heat of vaporization (ΔHᵥₐₚ).
Equation: q = mΔHᵥₐₚ

4. Condensation

Process: Gas to liquid.
Energy Change: Releases heat (exothermic).
Key Term: Heat of vaporization (ΔHᵥₐₚ), but negative.
Equation: q = −mΔHᵥₐₚ

5. Sublimation

Process: Solid to gas.
Energy Change: Absorbs heat (endothermic).
Key Term: Heat of sublimation $(\Delta H_{\text{sub}})$ .
Equation: $q= m\Delta H_{\text{sub}}$

6. Deposition

Process: Gas to solid.
Energy Change: Releases heat (exothermic).
Key Term: Heat of sublimation $\Delta H_{\text{sub}}$ , but negative.
Equation: $q = -m \Delta H_{\text{sub}}$

Heating and Cooling Curves

Heating and cooling curves graphically represent the changes in temperature of a substance as it absorbs or releases heat over time. These curves are essential for understanding phase transitions and the energy changes associated with them.

Heating Curve

A heating curve shows how the temperature of a substance increases as it absorbs heat. The curve includes distinct segments for each phase and phase change.

Heating Curve for Water

Solid Heating (Ice Warming)
- Temperature Range: Below 0°C.
- Equation: q = $m c_{\text{solid}} \Delta T$
- Key Point: Temperature rises steadily as heat is absorbed, increasing the kinetic energy of the particles.
Melting (Fusion)
- Temperature Range: 0°C.
- Equation: q = $m \Delta H_{\text{fus}}$
- Key Point: Temperature remains constant during the phase change as heat energy is used to break the bonds between solid particles, turning ice into liquid water.
Liquid Heating (Water Warming)
- Temperature Range: 0°C to 100°C.
- Equation: q = $m c_{\text{liquid}} \Delta T$
- Key Point: Temperature rises steadily as heat is absorbed, increasing the kinetic energy of the water molecules.
Vaporization (Boiling)
- Temperature Range: 100°C.
- Equation: q = $m \Delta H_{\text{vap}}$
- Key Point: Temperature remains constant during the phase change as heat energy is used to break the intermolecular forces between liquid particles, turning water into steam.
Gas Heating (Steam Warming)
- Temperature Range: Above 100°C.
- Equation: q = $m c_{\text{gas}} \Delta T$
- Key Point: Temperature rises steadily as heat is absorbed, increasing the kinetic energy of the steam particles.

Cooling Curve

A cooling curve shows how the temperature of a substance decreases as it releases heat. The curve includes distinct segments for each phase and phase change, similar to the heating curve but in reverse.

Cooling Curve for Water

Gas Cooling (Steam Cooling)
- Temperature Range: Above 100°C.
- Equation: q = $m c_{\text{gas}} \Delta T$
- Key Point: Temperature decreases steadily as heat is released, decreasing the kinetic energy of the steam particles.
Condensation
- Temperature Range: 100°C.
- Equation: q = $-m \Delta H_{\text{vap}}$
- Key Point: Temperature remains constant during the phase change as heat energy is released, allowing steam to condense into liquid water.
Liquid Cooling (Water Cooling)
- Temperature Range: 100°C to 0°C.
- Equation: q = $m c_{\text{liquid}} \Delta T$
- Key Point: Temperature decreases steadily as heat is released, decreasing the kinetic energy of the water molecules.
Freezing
- Temperature Range: 0°C.
- Equation: q = $-m \Delta H_{\text{fus}}$
- Key Point: Temperature remains constant during the phase change as heat energy is released, allowing liquid water to freeze into ice.
Solid Cooling (Ice Cooling)
- Temperature Range: Below 0°C.
- Equation: q = $m c_{\text{solid}} \Delta T$
- Key Point: Temperature decreases steadily as heat is released, decreasing the kinetic energy of the ice particles.

Steps for Calculating Energy for Phase Changes

Identify the Different Phases and Phase Changes
- Determine the initial and final states of the substance.
- Identify all phases the substance goes through.
- Note the temperature ranges and phase changes that occur.
Calculate Energy for Heating or Cooling within a Phase
- Use the specific heat capacity (c) to calculate the energy required to change the temperature within a single phase.
- Equation: q=mcΔT
  - q = heat energy (Joules)
  - m = mass (grams)
  - c = specific heat capacity (J/g°C)
  - ΔT = change in temperature (°C)
Calculate Energy for Phase Changes
- Use the heat of fusion (ΔHբᵤₛ) or heat of vaporization (ΔHᵥₐₚ) to calculate the energy required for phase changes.
- Equation: q = mΔH
  - q = heat energy (Joules)
  - m = mass (grams)
  - ΔH = heat of phase change (J/g)
Sum the Energy Values
- Add all the energy values from each step to find the total energy required for the entire process.
- Equation: qₜₒₜₐₗ = q₁ + q₂ + q₃ + q₄ + q₅
  - $q_{\text{total}}$ = total heat energy (Joules)
  - q₁, q₂, q₃, q₄, q₅ = heat energy for each segment of the process (Joules)

Example Problem

Calculate the total energy required to convert 50 g of ice at -10°C to steam at 120°C.

Steps for Calculation

Identify the Different Phases and Phase Changes
- Initial state: Ice at -10°C.
- Final state: Steam at 120°C.
- Phases and changes:
  - Heating ice from -10°C to 0°C.
  - Melting ice at 0°C.
  - Heating water from 0°C to 100°C.
  - Vaporizing water at 100°C.
  - Heating steam from 100°C to 120°C.
Calculate Energy for Heating or Cooling within a Phase
- Heating Ice from -10°C to 0°C
  - $c_{\text{solid}} = 2.1 \, \frac{\text{J}}{\text{g} \cdot \text{°C}}$
  - $q_1 = 50 \, \text{g} \times 2.1 \, \frac{\text{J}}{\text{g} \cdot \text{°C}} \times 10 \, \text{°C} = 1050 \, \text{J}$
- Heating Water from 0°C to 100°C
  - $c_{\text{liquid}} = 4.18 \, \frac{\text{J}}{\text{g} \cdot \text{°C}}$
  - $q_3 = 50 \, \text{g} \times 4.18 \times 100 = 20900 \, \text{J}$
- Heating Steam from 100°C to 120°C
  - $c_{\text{gas}} = 2.0 \, \frac{\text{J}}{\text{g} \cdot \text{°C}}$
  - $q_5 = 50 \, \text{g} \times 2.0 \times 20 = 2000 \, \text{J}$
Calculate Energy for Phase Changes
- Melting Ice at 0°C
  - $\Delta H_{\text{fus}} = 334 \, \frac{\text{J}}{\text{g}}$
  - $q_2 = 50 \, \text{g} \times 334 = 16700 \, \text{J}$
- Vaporizing Water at 100°C
  - $\Delta H_{\text{vap}} = 2260 \, \frac{\text{J}}{\text{g}}$
  - $q_4 = 50 \, \text{g} \times 2260 = 113000 \, \text{J}$
Sum the Energy Values
- Total energy required: $q_{\text{total}} = q_1 + q_2 + q_3 + q_4 + q_5$
- $q_{\text{total}} = 1050 \, \text{J} + 16700 \, \text{J} + 20900 \, \text{J} + 113000 \, \text{J} + 2000 \, \text{J} = 153650 \, \text{J}$