Resonance and Formal Charge

Learning Objectives

By studying resonance and formal charge for the AP Chemistry exam, you should be able to understand and apply the concept of electron delocalization in molecules, identify and draw multiple resonance structures, and determine the resonance hybrid. You should learn how to calculate formal charges for atoms in a molecule using the appropriate formula, and use these calculations to evaluate the stability of different resonance structures. Additionally, you should understand how resonance and formal charge influence molecular geometry, bond lengths, bond energies, and overall molecular stability, aiding in predicting the reactivity and properties of compounds.

Introduction

Resonance and formal charge are fundamental concepts in chemistry that explain the stability and electron distribution in molecules. Resonance describes the delocalization of electrons across multiple atoms, leading to structures that cannot be represented by a single Lewis structure. Formal charge helps determine the most stable resonance structure by calculating the charge distribution on each atom. Together, these concepts provide a deeper understanding of molecular geometry, reactivity, and properties.

Resonance

What is Resonance?

Resonance is a phenomenon in chemistry where a molecule or ion is best described by two or more valid Lewis structures, known as resonance structures. These structures differ only in the placement of electrons, not the arrangement of atoms. The actual molecule is a resonance hybrid, representing the delocalization of electrons across the atoms, which contributes to the molecule’s stability.

Key Points

1. Multiple Structures: Resonance involves two or more valid Lewis structures for a single molecule or ion, called resonance structures.
2. Electron Delocalization: Electrons are shared over multiple atoms rather than being confined to a single bond or lone pair.
3. Stability: The resonance hybrid, which is the actual structure of the molecule, is more stable than any individual resonance structure due to electron delocalization.
4. Representation: Resonance structures are depicted using double-headed arrows (↔) between them.
5. Bond Characteristics: In the resonance hybrid, bond lengths and strengths are intermediate between those depicted in the individual resonance structures.
6. Resonance Energy: The extra stability gained from resonance is called resonance energy.
7. Influence on Properties: Resonance affects various molecular properties, such as bond length, bond energy, and reactivity.

Importance of Resonance

1. Increased Stability: Resonance delocalizes electrons over multiple atoms, reducing electron repulsion and enhancing the overall stability of the molecule.
2. Bond Length Uniformity: It leads to bond lengths that are intermediate between single and double bonds, providing a more accurate representation of molecular structure.
3. Energy Distribution: Resonance spreads the molecule’s potential energy over a larger volume, lowering its overall energy.
4. Predicting Reactivity: Understanding resonance helps predict how molecules will react, as the delocalized electrons often participate in chemical reactions.
5. Explaining Molecular Properties: Resonance is key to explaining various physical and chemical properties, such as acidity, basicity, and color.
6. Molecular Symmetry: Resonance contributes to the symmetry of certain molecules, which is crucial for understanding their behavior in different chemical environments.
7. Chemical Bonding Theory: It is essential in advanced theories of chemical bonding, such as Molecular Orbital Theory, which requires an understanding of electron delocalization.

Examples

Benzene (C₆H₆)

Benzene has two primary resonance structures where the double bonds alternate around the ring. The resonance hybrid shows delocalized π electrons above and below the plane of the ring.

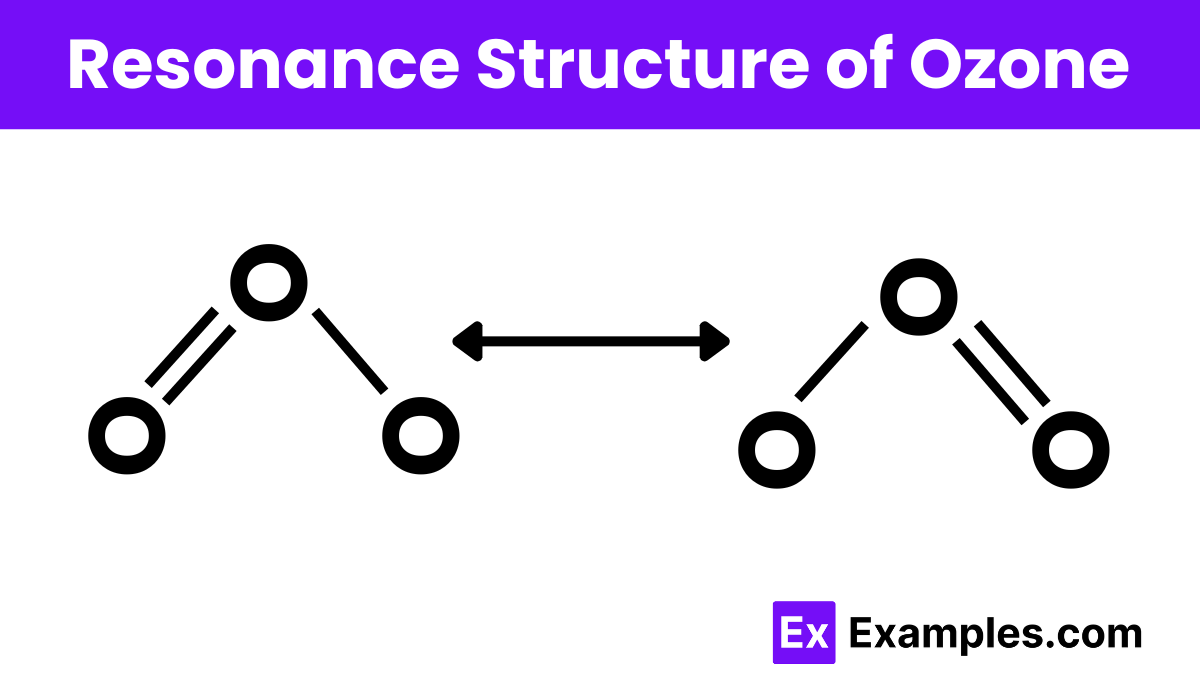
Ozone (O₃)

Ozone has two resonance structures:

• Structure 1: O=O-O⁻
• Structure 2: O⁻-O=O

In these structures, the positions of the double and single bonds switch. The resonance hybrid indicates that each O-O bond has a bond order of 1.5, reflecting partial double-bond character.

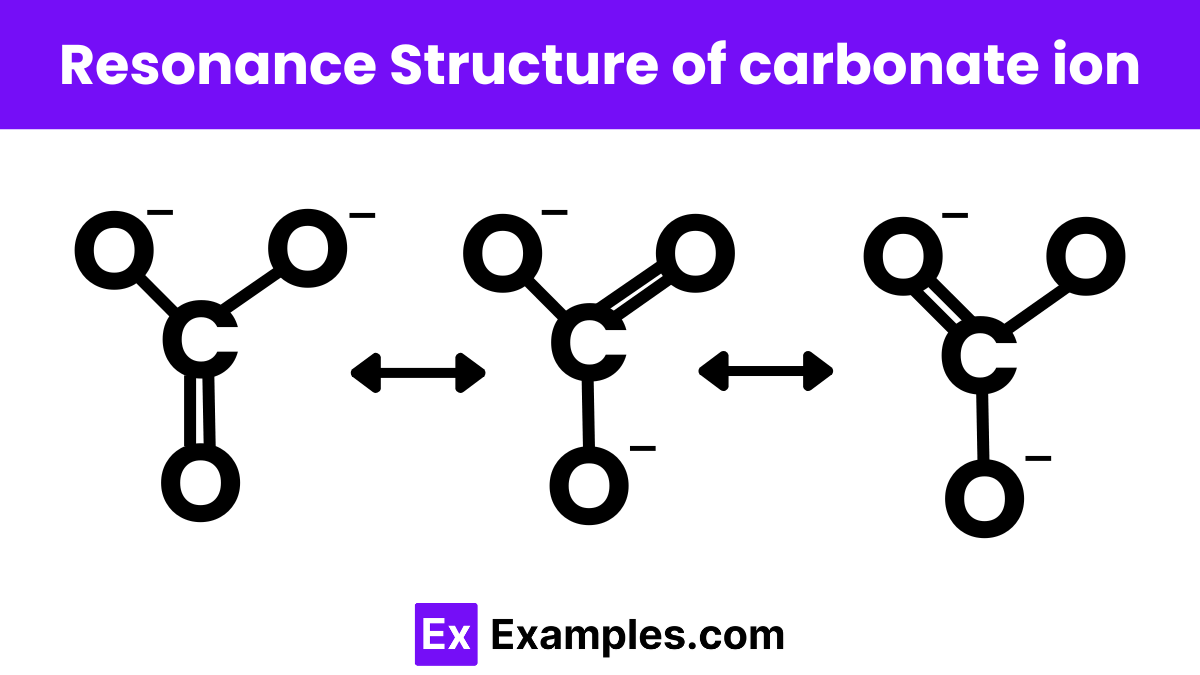
3. Carbonate Ion (CO₃²⁻)

The carbonate ion (CO₃²⁻) has three resonance structures:

• Structure 1: O=C-O⁻
• Structure 2: O⁻-C=O
• Structure 3: O-C=O⁻

In each structure, one of the oxygen atoms carries a negative charge while being bonded to the carbon with a single bond, and the other two bonds are double bonds. The resonance hybrid shows that all three C-O bonds are equivalent, with a bond order of approximately 1⅓.

Formal Charges

What is Formal Charge?

Formal charge is a theoretical concept used in chemistry to estimate the distribution of electrons in a molecule. It represents the difference between the number of valence electrons in an isolated atom and the number of electrons assigned to that atom in a Lewis structure. The formal charge is calculated using the formula:

Steps to Calculate Formal Charge

1. Determine Valence Electrons: Identify the number of valence electrons for the atom.
2. Count Non-bonding Electrons: Count the lone pair electrons on the atom.
3. Count Bonding Electrons: Count the total number of electrons in bonds with other atoms, then divide by two.
4. Apply Formula: Use the formula Formal Charge =

Importance of Formal Charge

1. Determining Stability: Helps identify the most stable Lewis structure by minimizing formal charges.
2. Predicting Reactivity: Indicates regions of high electron density or positive charge, predicting sites of chemical reactivity.
3. Identifying Resonance Structures: Assists in evaluating and comparing the stability of different resonance structures.
4. Molecular Polarity: Contributes to understanding the distribution of charges within a molecule, influencing its polarity.
5. Guiding Chemical Bonding: Helps in understanding the electron distribution within bonds, guiding predictions about bond strength and length.
6. Explaining Molecular Geometry: Aids in predicting the geometry of molecules by considering formal charge distribution.
7. Optimizing Molecule Design: Essential in designing molecules with desired properties in fields like pharmaceuticals and materials science.

Examples

Formal Charge in Water (H₂O)

• Oxygen (O):
  • Valence electrons: 6
  • Non-bonding electrons: 4 (2 lone pairs)
  • Bonding electrons: 4 (2 bonds with hydrogen)
  • = 6 – (4 + 2) = 0
• Hydrogen (H) (each):
  • Valence electrons: 1
  • Non-bonding electrons: 0
  • Bonding electrons: 2 (1 bond with oxygen)
  • = 1 – 1 = 0

2. Formal Charge in Ammonium Ion (NH₄⁺)

• Nitrogen (N):
  • Valence electrons: 5
  • Non-bonding electrons: 0
  • Bonding electrons: 8 (4 bonds with hydrogen)
  • = 5 – 4 = +1
• Hydrogen (H) (each):
  • Valence electrons: 1
  • Non-bonding electrons: 0
  • Bonding electrons: 2 (1 bond with nitrogen)
  • = 1 – 1 = 0

3. Formal Charge in Carbonate Ion (CO₃²⁻)

• Carbon (C):
  • Valence electrons: 4
  • Non-bonding electrons: 0
  • Bonding electrons: 8 (4 bonds with oxygen)
  • = 4 – 4 = 0
• Oxygen (O) (double-bonded):
  • Valence electrons: 6
  • Non-bonding electrons: 4 (2 lone pairs)
  • Bonding electrons: 4 (2 bonds with carbon)
  • = 6 – 6 = 0
• Oxygen (O) (single-bonded, each):
  • Valence electrons: 6
  • Non-bonding electrons: 6 (3 lone pairs)
  • Bonding electrons: 2 (1 bond with carbon)
  • = 6 – 7 = -1

Comparing Resonance Structures Using Formal Charge

When evaluating resonance structures, formal charge is a critical tool for determining which structures contribute most significantly to the resonance hybrid. Here’s how to compare resonance structures using formal charge:

Steps to Compare Resonance Structures

1. Calculate Formal Charge: Determine the formal charge for each atom in all resonance structures.
2. Minimize Formal Charges: Structures with formal charges closest to zero are generally more stable.
3. Electronegativity Consideration: Place negative formal charges on more electronegative atoms and positive charges on less electronegative atoms.
4. Avoid Like Charges: Structures that have like charges (both positive or both negative) on adjacent atoms are less favorable.

Example: Nitrite Ion (NO₂⁻)

Nitrite ion has two resonance structures:

1. Structure 1:
   • O=N-O⁻
2. Structure 2:
   • O⁻-N=O

Formal Charge Calculation:

• Structure 1:
  • Nitrogen (N): = 5 – 4 = +1
  • Double-bonded Oxygen (O): = 6 – 6 = 0
  • Single-bonded Oxygen (O): = 6 – 7 = -1
• Structure 2:
  • Nitrogen (N): Formal Charge= = 5 – 4 = +1
  • Double-bonded Oxygen (O): = 6 – 6 = 0
  • Single-bonded Oxygen (O): = 6 – 7 = -1

Comparison:

Both resonance structures for NO₂⁻ have the same formal charges on each atom:

• Nitrogen (N) has a formal charge of +1.
• Double-bonded Oxygen (O) has a formal charge of 0.
• Single-bonded Oxygen (O) has a formal charge of -1.

Since both structures have identical formal charges, they are equally significant in contributing to the resonance hybrid.