Searching and Sorting Using Binary Search and Merge Sort Algorithms

Binary Search and Merge Sort are fundamental algorithms in computer science, particularly useful for efficiently searching and sorting data. Binary Search operates on sorted arrays and utilizes a divide-and-conquer approach to find elements in O(log n) time by repeatedly halving the search space. Merge Sort, another divide-and-conquer algorithm, recursively divides an array into subarrays, sorts them, and merges them back together, achieving O(n log n) time complexity. Both algorithms are essential for optimizing performance in data processing and problem-solving in computer science.

Learning Objectives

For the topic “Searching and Sorting Using Binary Search and Merge Sort Algorithms”, in AP Computer Science A” you should focus on understanding how binary search efficiently finds elements in a sorted array using divide-and-conquer principles, with a time complexity of O(log n). Additionally, learn the structure and recursive process of merge sort, its time complexity of O(n log n), and its ability to merge two sorted sub-arrays. You should be able to write and analyze code for both algorithms, understanding their efficiency and practical applications in solving computational problems.

Binary Search Algorithm

Overview: Binary search is an efficient algorithm for finding a target value within a sorted array. It works by repeatedly dividing the search interval in half and eliminating half of the remaining elements in each step. The time complexity of binary search is O(logn), making it very efficient for large datasets.

Steps in Binary Search:

• Initial Setup:
  • The array must be sorted.
  • Set two pointers, low to the first index and high to the last index of the array.
• Iteration Process:
  • Calculate the middle index: mid = (low + high) / 2.
  • Compare the target value with the middle element.
  • If the target equals the middle element, return the middle index (found).
  • If the target is less than the middle element, set high = mid – 1 (narrow search to the left half).
  • If the target is greater than the middle element, set low = mid + 1 (narrow search to the right half).
• Termination:
  • The algorithm continues dividing the array until the target is found, or the low pointer exceeds the high pointer, indicating that the target is not in the array.

Binary Search Code Example (in Java)

public class BinarySearch {
    public static int binarySearch(int[] arr, int target) {
        int low = 0;
        int high = arr.length - 1;
        while (low <= high) {
            int mid = (low + high) / 2;
            if (arr[mid] == target) {
                return mid; // Target found
            } else if (arr[mid] < target) {
                low = mid + 1; // Search in the right half
            } else {
                high = mid - 1; // Search in the left half
            }
        }
        return -1; // Target not found
    }
}

Merge Sort Algorithm

Overview: Merge Sort is a highly efficient, comparison-based, divide-and-conquer sorting algorithm. It recursively divides the array into two halves, sorts each half, and then merges the sorted halves to produce the final sorted array. Merge Sort operates with a time complexity of O(nlogn), making it suitable for large datasets.

Steps in Merge Sort:

• Divide: Recursively split the array into two halves until each sub-array contains a single element.
• Conquer: Recursively sort the two halves. Each step calls merge sort on the left and right halves until all the single-element arrays are merged back.
• Merge: Combine two sorted halves into a single sorted array. This merging process ensures the final output is sorted.

Merge Process:

• Compare the first elements of the left and right halves.
• Append the smaller element to the result.
• Continue this process until one of the halves is exhausted.
• Append the remaining elements from the other half.
• Merge the elements back into the original array, maintaining sorted order.Recursively repeat the merge process until the entire array is sorted.

Merge Sort Code Example (in Java)

public class MergeSort {
    // Function to merge two halves
    public static void merge(int[] arr, int[] left, int[] right) {
        int i = 0, j = 0, k = 0;
        while (i < left.length && j < right.length) {
            if (left[i] <= right[j]) {
                arr[k++] = left[i++];
            } else {
                arr[k++] = right[j++];
            }
        }
        while (i < left.length) {
            arr[k++] = left[i++];
        }
        while (j < right.length) {
            arr[k++] = right[j++];
        }
    }

    // Main Merge Sort function
    public static void mergeSort(int[] arr) {
        if (arr.length < 2) {
            return;
        }
        int mid = arr.length / 2;
        int[] left = new int[mid];
        int[] right = new int[arr.length - mid];

        // Copy data to left and right arrays
        System.arraycopy(arr, 0, left, 0, mid);
        System.arraycopy(arr, mid, right, 0, arr.length - mid);

        // Recursively sort both halves
        mergeSort(left);
        mergeSort(right);

        // Merge sorted halves
        merge(arr, left, right);
    }
}

Advantages and Disadvantages of Merge Sort

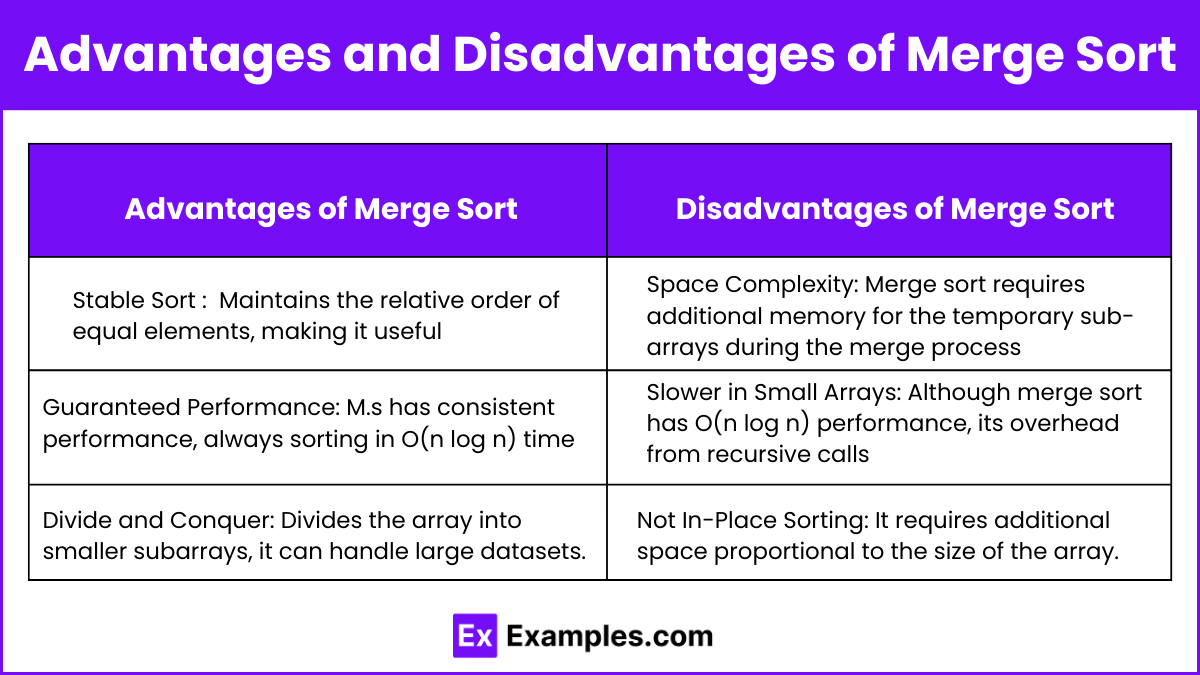
Advantages of Merge Sort:

• Stable Sort: Maintains the relative order of equal elements, making it useful when preserving order is important.
• Guaranteed O(n log n) Performance: Merge sort has consistent performance, always sorting in O(n log n) time, regardless of the input data’s initial order, unlike algorithms like quicksort, which can degrade to O(n²) in the worst case.
• Divide and Conquer: Since merge sort divides the array into smaller sub-arrays, it can handle large datasets more efficiently. This divide-and-conquer approach also allows for parallel processing if implemented.

Disadvantages of Merge Sort:

• Space Complexity: Merge sort requires additional memory for the temporary sub-arrays during the merge process, resulting in O(n) space complexity. This can be inefficient for large datasets where memory usage is a concern.
• Slower in Small Arrays: Although merge sort has O(n log n) performance, its overhead from recursive calls and extra memory allocation can make it slower compared to other algorithms like quicksort or insertion sort for smaller arrays.
• Not In-Place Sorting: Merge sort is not an in-place algorithm, meaning it requires additional space proportional to the size of the array. This increases the memory footprint, which may not be ideal in memory-constrained environments.

Examples

Example 1: Student Exam Scores Analysis

Imagine a scenario where a teacher has a list of students’ exam scores sorted in ascending order. The teacher wants to quickly find if a specific student’s score exists in the list. By using binary search, the teacher can efficiently determine the score’s presence by halving the search space with each iteration, rather than scanning through the entire list.

Example 2: Organizing Library Books

A digital library system manages thousands of books, sorted alphabetically by title. When a user searches for a specific book title, binary search can quickly locate the exact book by dividing the sorted list of titles in half repeatedly. Additionally, if the book titles need to be sorted, the system can employ merge sort to handle even large datasets efficiently, ensuring the list is organized properly for future searches.

Example 3: Inventory Management System

In a warehouse, the stock-keeping unit (SKU) numbers of items are stored in a sorted list. When checking whether a particular SKU exists in the inventory, binary search can be used to efficiently search through the list and retrieve the item’s details without having to examine every item sequentially. When the inventory is updated with new items, merge sort can be used to maintain the sorted order of the SKU numbers.

Example 5: Medical Records Search

In a hospital database, patient medical records are sorted by patient ID numbers. To quickly locate a patient’s record based on their ID, a binary search can be applied, reducing the time needed to retrieve the correct record. If the records are received out of order or need to be reorganized, merge sort is ideal for sorting large numbers of records, ensuring the database remains efficient for future queries.

Example 6: Financial Data Sorting and Searching

A financial institution tracks the daily stock prices of various companies over a year. The data needs to be sorted by the closing price so analysts can study trends. Merge sort can be used to sort this large dataset efficiently. When an analyst wants to check whether a certain stock hit a specific price on a given day, binary search can be employed to quickly locate the price within the sorted list.

Multiple Choice Questions

Question 1

What is the time complexity of the binary search algorithm when searching for an element in a sorted array?

A) O(n)
B) O(n log n)
C) O(log n)
D) O(n²)

Answer: C) O(log n)

Explanation: Binary search works by repeatedly dividing the search interval in half. Since the array is already sorted, each comparison allows you to eliminate half of the remaining elements, leading to a logarithmic number of comparisons. Therefore, the time complexity of binary search is O(log n). It is much faster than linear search for large datasets.

Question 2

Which of the following best describes the merge step in the merge sort algorithm?

A) Dividing the array into smaller sub-arrays
B) Merging two unsorted sub-arrays into a single sorted array
C) Combining two sorted sub-arrays into a single sorted array
D) Sorting a single element from the array

Answer: C) Combining two sorted sub-arrays into a single sorted array

Explanation: Merge sort is a divide-and-conquer algorithm. The merge step occurs after the array has been divided into smaller sub-arrays, and it involves combining two sorted sub-arrays into a single sorted array. The merge process ensures that the overall array remains sorted as the sub-arrays are combined.

Question 3

What is the key difference between merge sort and binary search in terms of their application?

A) Binary search sorts an array, whereas merge sort searches for an element in the array.
B) Merge sort requires the array to be sorted, whereas binary search does not.
C) Binary search works on sorted arrays, whereas merge sort sorts arrays.
D) Merge sort has a worse time complexity than binary search in all cases.

Answer: C) Binary search works on sorted arrays, whereas merge sort sorts arrays

Explanation: Binary search is a search algorithm that requires the input array to be sorted before it can work. It efficiently finds an element’s position by dividing the search space in half at each step. Merge sort, on the other hand, is a sorting algorithm that sorts an unsorted array using the divide-and-conquer approach. Therefore, merge sort prepares the data, while binary search operates on sorted data.