Angular Momentum and Torque
Understanding angular momentum and torque is crucial for mastering rotational dynamics and achieving a high score on the AP Physics exam. These concepts are fundamental in analyzing the motion of rotating objects and the forces that cause changes in rotational motion. Below are detailed notes to help you excel in this topic.
Learning Objectives
In the AP Physics exam, students should understand the principles of Conservation of Energy, the Work–Energy Principle, and Power. This includes comprehending how energy is conserved in isolated systems, applying the work-energy theorem to solve problems, and calculating power as the rate of energy transfer. Additionally, students should be able to analyze real-world scenarios using these concepts, perform calculations involving kinetic and potential energy, and understand the implications of energy transformations and efficiency in physical systems.
Angular Momentum
Definition: Angular momentum (L) is the rotational analogue of linear momentum. It is a measure of the quantity of rotation an object has, taking into account its moment of inertia and angular velocity.
Characteristics
- Vector Quantity: Direction is perpendicular to the plane of rotation, following the right-hand rule.
- Conservation: In the absence of external torques, the total angular momentum of a system remains constant.
Angular Momentum of a Particle
Formula: L = r × p
where:
- L is the angular momentum,
- r is the position vector of the particle relative to the axis of rotation,
- p is the linear momentum of the particle (p = mv),
- × denotes the cross product.
Angular Momentum of a Rigid Body
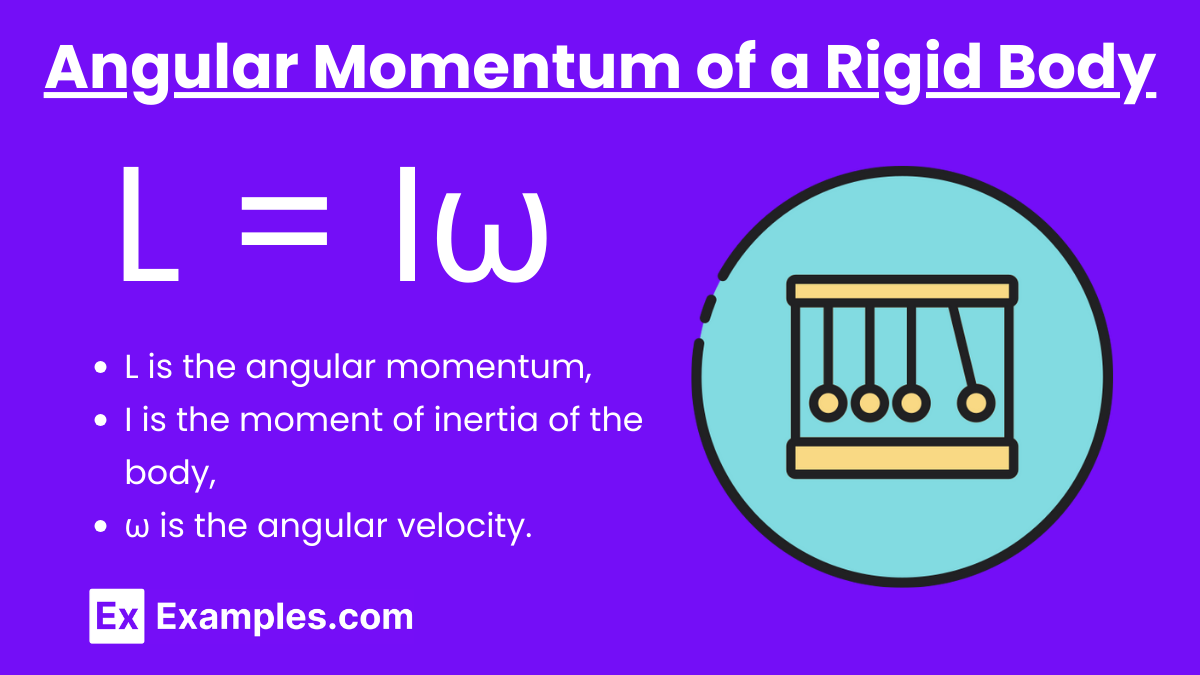
Formula: L = Iω
where:
- L is the angular momentum,
- I is the moment of inertia of the body,
- ω is the angular velocity.
Key Points:
- Angular momentum is a vector quantity, having both magnitude and direction.
- The direction of the angular momentum vector is perpendicular to the plane of rotation.
Conservation of Angular Momentum
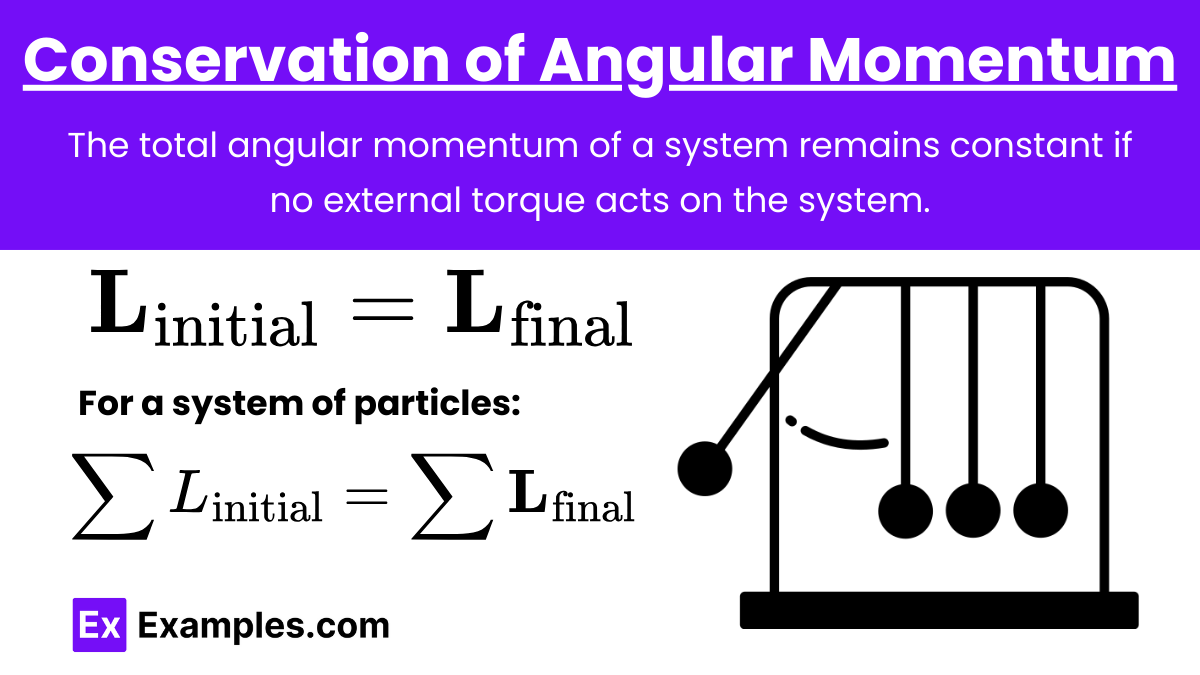
Principle: The total angular momentum of a system remains constant if no external torque acts on the system.
Formula: \[ \mathbf{L}_{\text{initial}} = \mathbf{L}_{\text{final}} \]
Example: A figure skater spins faster when pulling in their arms. Here, the moment of inertia decreases, so the angular velocity increases to conserve angular momentum.
Torque
Definition: Torque (τ) is the rotational analogue of force. It is a measure of the tendency of a force to cause an object to rotate about an axis.
Characteristics
- Vector Quantity: Direction is determined by the right-hand rule.
- Moment Arm: The perpendicular distance from the axis of rotation to the line of action of the force.
Formula
τ = r×F
where:
- τ is the torque,
- r is the position vector from the axis of rotation to the point where the force is applied,
- F is the applied force,
- × denotes the cross product.
Magnitude of Torque: τ = rFsinθ
where:
- τ is the magnitude of the torque,
- r is the distance from the axis of rotation to the point where the force is applied,
- F is the magnitude of the force,
- θ is the angle between r and F.
Key Points:
- Torque is a vector quantity, having both magnitude and direction.
- The direction of the torque vector is determined by the right-hand rule.
Relationship Between Torque and Angular Acceleration
Formula: τ = Iα
where:
- τ is the net torque,
- I is the moment of inertia,
- α is the angular acceleration.
Key Points:
- A net torque acting on a body causes an angular acceleration, similar to how a net force causes linear acceleration.
Moment of Inertia
Definition: Moment of inertia (I) is a measure of an object’s resistance to changes in its rotational motion.
Formula for a Point Mass: I = mr²
where:
- m is the mass of the object,
- r is the distance from the axis of rotation.
Formulas for Common Geometries:
- Solid sphere: \[ I = \frac{2}{5}mr^2 \]
- Solid cylinder: \[ I = \frac{1}{2}mr^2 \]
- Thin rod (about center): \[ I = \frac{1}{12}ml^2 \]
- Thin rod (about end): \[ I = \frac{1}{3}ml^2 \]
Examples
Example 1: Calculating Angular Momentum of a Particle
Scenario: A particle of mass 2kg is moving with a velocity of 3m/s at a distance of 4m from the axis of rotation.
Solution: \[ \mathbf{L} = \mathbf{r} \times \mathbf{p} = rmv \sin \theta \] \[ \text{Assuming } \theta = 90^\circ, \] \[ L = 4 \times 2 \times 3 \times \sin 90^\circ = 24 \, \text{kg} \cdot \text{m}^2/\text{s} \]
Example 2: Conservation of Angular Momentum
Scenario: A figure skater with moment of inertia I₁ and angular velocity ω₁ pulls in her arms, reducing her moment of inertia to \[ I_2 = \frac{1}{2} I_1 \]. Calculate her new angular velocity ω₂.
Solution: \[ \mathbf{L}_{\text{initial}} = \mathbf{L}_{\text{final}} \] \[ I_1 \omega_1 = I_2 \omega_2 \] \[ \omega_2 = \frac{I_1 \omega_1}{I_2} = \frac{I_1 \omega_1}{\frac{1}{2} I_1} = 2 \omega_1 \]
Example 3: Calculating Torque
Scenario: A force of 10N is applied at a distance of 0.5m from the axis of rotation, making an angle of 30ᵒ with the lever arm.
Solution: τ = rFsinθ
τ = 0.5×10×sin30ᵒ = 0.5×10×0.5 = 2.5N⋅m
Example 4: Earth’s Rotation
The Earth rotating about its axis.
- Moment of Inertia (I): Depends on Earth’s mass distribution.
- Angular Velocity (ω): Constant for Earth’s rotation.
L = Iω
Example 5: Rolling Disk
A disk of mass m and radius R rolls without slipping.
- Linear Velocity (v) of center of mass: Related to angular velocity by v=Rω.
- Angular Momentum (L): Sum of translational and rotational angular momentum.
L = Iω+mvR
Applications
1. Engineering and Machinery
- Rotational Devices: Understanding angular momentum and torque is essential in designing gears, turbines, and flywheels.
- Balancing Rotating Systems: Ensuring the stability of rotating machinery by balancing angular momentum and minimizing unwanted torques.
2. Sports
- Diving and Gymnastics: Athletes control their body positions to manage angular momentum, performing flips and twists.
- Cycling: Cyclists apply torque to the pedals, generating angular momentum in the wheels.
3. Aerospace
- Satellite Stabilization: Satellites use gyroscopes to maintain orientation by conserving angular momentum.
- Spacecraft Maneuvers: Thrusters apply torque to change the angular momentum of spacecraft, adjusting their orientation.
4. Everyday Life
- Opening Doors: Applying force at the edge of a door creates torque, making it easier to open compared to pushing near the hinge.
- Wrenches and Tools: Using a longer wrench increases the torque applied to a bolt, making it easier to turn.
Practice Problems
Question 1:
Which of the following statements is true about angular momentum?
A) Angular momentum is always conserved.
B) Angular momentum depends on the object’s mass, velocity, and radius from the axis of rotation.
C) Angular momentum is a scalar quantity.
D) Angular momentum is always zero for objects moving in a straight line.
Answer: B) Angular momentum depends on the object’s mass, velocity, and radius from the axis of rotation.
Explanation: Angular momentum (L) of an object is given by the formula L = Iω or L = mvr for a point mass, where m is mass, v is linear velocity, and r is the radius or distance from the axis of rotation. This makes option B correct. Angular momentum is not always conserved (option A) unless the net external torque is zero. It is a vector quantity (option C), not scalar. Objects moving in a straight line can have angular momentum if considered about a point not on the line of motion (option D).
Question 2:
What is the effect of doubling the radius on the torque applied to a rotating object if the force remains constant?
A) Torque is halved.
B) Torque remains unchanged.
C) Torque is doubled.
D) Torque is quadrupled.
Answer: C) Torque is doubled.
Explanation: Torque (τ) is calculated using the formula τ = rFsin(θ), where r is the radius, F is the force applied, and θ is the angle between the force vector and the lever arm. If the force remains constant and the radius is doubled, the torque will also double. Thus, option C is correct.
Question 3:
If a figure skater pulls in their arms while spinning, what happens to their angular velocity and why?
A) Angular velocity decreases due to increased moment of inertia.
B) Angular velocity remains constant because angular momentum is not conserved.
C) Angular velocity increases due to decreased moment of inertia.
D) Angular velocity decreases because torque is applied.
Answer: C) Angular velocity increases due to decreased moment of inertia.
Explanation: When a figure skater pulls in their arms, they reduce their moment of inertia (I). According to the conservation of angular momentum (L = Iω), if no external torque acts on the system, the product of the moment of inertia and angular velocity (ω) must remain constant. Therefore, a decrease in moment of inertia results in an increase in angular velocity. Thus, option C is correct.