Centripetal Acceleration vs. Centripetal Force
Understanding centripetal acceleration and centripetal force is crucial for mastering the concepts of circular motion in the AP Physics exam. These concepts explain the forces and accelerations acting on objects moving in circular paths. Below are detailed notes to help you achieve a high score on your AP Physics exam.
Learning Objectives
By studying Centripetal Acceleration vs. Centripetal Force for the AP Physics exam, you will learn to differentiate between the two concepts, understand their mathematical definitions, and grasp how they relate to circular motion. You’ll explore how centripetal acceleration keeps an object moving in a circular path, while centripetal force is the net force causing this acceleration. Additionally, you will learn to apply relevant formulas, analyze real-world examples, and solve problems involving these principles to prepare for the exam.
Centripetal Acceleration
Definition: Centripetal acceleration is the acceleration of an object moving in a circular path, directed towards the center of the circle. It is responsible for changing the direction of the object’s velocity.
Formula:
\[ a_c = \frac{v^2}{r} \]
where:
- a꜀ is the centripetal acceleration,
- v is the tangential velocity of the object,
- r is the radius of the circular path.
Key Points:
- Centripetal acceleration always points towards the center of the circle.
- It is perpendicular to the object’s velocity.
- It does not change the speed of the object, only its direction.
Characteristics
- Direction: Always points toward the center of the circle.
- Magnitude: Depends on the square of the speed and inversely on the radius.
- Role: Keeps the object moving in a circular path by constantly changing its direction.
Examples
- Car Turning in a Circle:
When a car turns in a circular path, the centripetal acceleration keeps it moving along the curved trajectory. - Planet Orbiting the Sun:
The gravitational force provides the centripetal acceleration necessary for the planet to orbit the sun.
Centripetal Force
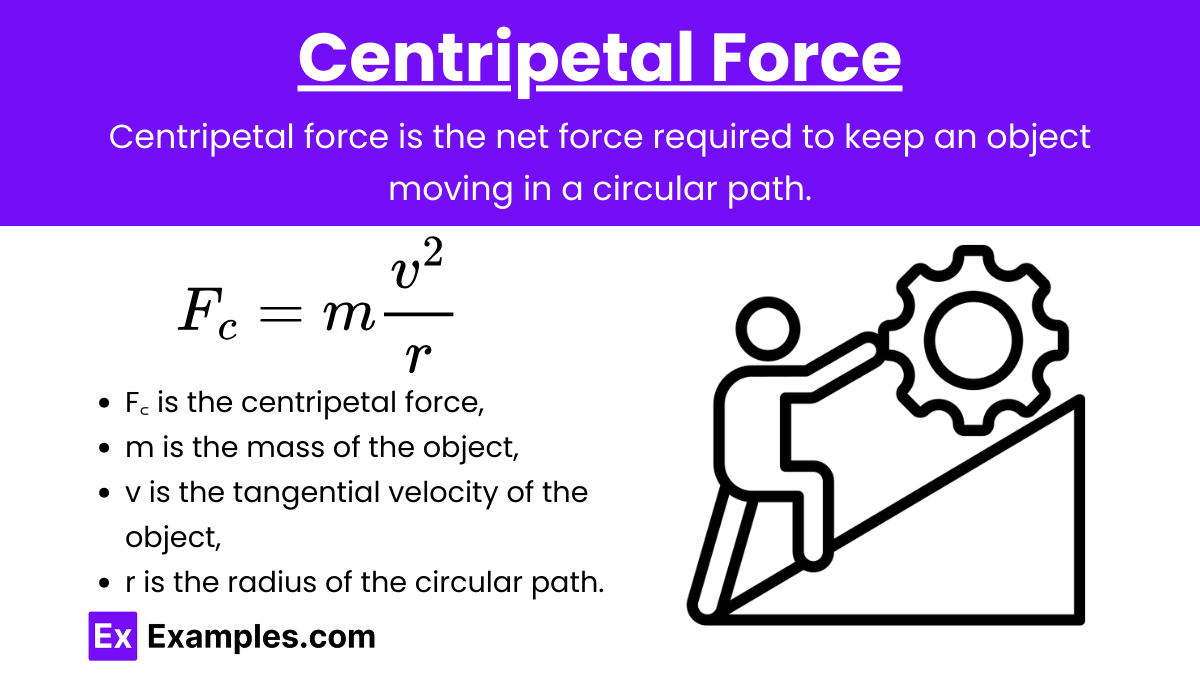
Definition: Centripetal force is the net force required to keep an object moving in a circular path. It acts towards the center of the circle and is responsible for maintaining circular motion.
Formula:
\[ F_c = m \frac{v^2}{r} \]
where:
- F꜀ is the centripetal force,
- m is the mass of the object,
- v is the tangential velocity of the object,
- r is the radius of the circular path.
Key Points
- Centripetal force is not a new type of force but the name for the net force causing circular motion.
- It can be the result of tension, gravity, friction, or other forces.
- Like centripetal acceleration, it always points towards the center of the circle.
Characteristics
- Direction: Always points toward the center of the circle.
- Magnitude: Depends on the mass, speed, and radius.
- Source: Can arise from various forces (e.g., tension, gravity, friction).
Examples
- Tension in a String:
- When a ball is swung in a circle on a string, the tension in the string provides the centripetal force.
- Gravitational Force:
- For a satellite orbiting Earth, gravity provides the centripetal force keeping it in orbit.
Relationship Between Centripetal Acceleration and Centripetal Force
Connection: Centripetal force is the force that causes centripetal acceleration. According to Newton’s Second Law, F=ma, the centripetal force can be calculated by multiplying the mass of the object by the centripetal acceleration.
\[ F_c = m a_c \]
\[ F_c = m \frac{v^2}{r} \]
Examples and Problems
Example 1: Car on a Circular Track
Scenario: A car of mass 1500 kg moves at a speed of 20 m/s around a circular track with a radius of 50 m. Calculate the centripetal acceleration and the centripetal force.
Solution:
- Centripetal acceleration: \[ a_c = \frac{v^2}{r} = \frac{(20 \, \text{m/s})^2}{50 \, \text{m}} = 8 \, \text{m/s}^2 \]
- Centripetal force: F꜀ = ma꜀ = 1500kg×8m/s² = 12000N
Example 2: Satellite in Orbit
Scenario: A satellite of mass 1000 kg orbits Earth at a speed of 7000 m/s at an altitude where the radius of its orbit is 7000 km. Calculate the centripetal acceleration and the centripetal force.
Solution:
- Convert radius to meters: 7000km=7×10⁶m
- Centripetal acceleration: \[ a_c = \frac{v^2}{r} = \frac{(7000 \, \text{m/s})^2}{7 \times 10^6 \, \text{m}} = 7 \, \text{m/s}^2 \]
- Centripetal force: F꜀ = ma꜀ = 1000kg×7m/s² = 7000N
Example 3: Ball on a String
Scenario: A 0.5 kg ball is swung in a horizontal circle at the end of a 1.5 m string at a speed of 5 m/s. Calculate the centripetal acceleration and the centripetal force.
Solution:
- Centripetal acceleration: \[ a_c = \frac{v^2}{r} = \frac{(5 \, \text{m/s})^2}{1.5 \, \text{m}} = 16.67 \, \text{m/s}^2 \]
- Centripetal force: F꜀ =ma꜀ = 0.5kg×16.67m/s² = 8.33N