Conservation of Angular Momentum
Understanding the principle of conservation of angular momentum is crucial for mastering rotational dynamics and achieving a high score on the AP Physics exam. This principle explains how the angular momentum of a system remains constant if no external torques act on it. Below are detailed notes to help you excel in this topic.
Learning Objectives
For the AP Physics exam, you should understand the principle of conservation of angular momentum, including its definition and applications. Learn how to calculate angular momentum for rotating objects, comprehend the relationship between torque and angular momentum, and solve problems involving rotational collisions and isolated systems. Recognize scenarios where angular momentum is conserved and analyze the effects of external torques. Practice applying these principles to real-world examples and AP-style questions to strengthen your problem-solving skills.
Angular Momentum
Angular Momentum (L): Angular momentum is a vector quantity that represents the rotational analog of linear momentum. It is defined as the product of an object’s moment of inertia and its angular velocity.
For a Point Mass
Formula: L = r×p
L = r×(mv)
where:
- L is the angular momentum,
- r is the position vector,
- p is the linear momentum,
- m is the mass,
- v is the velocity.
For a Rigid Body
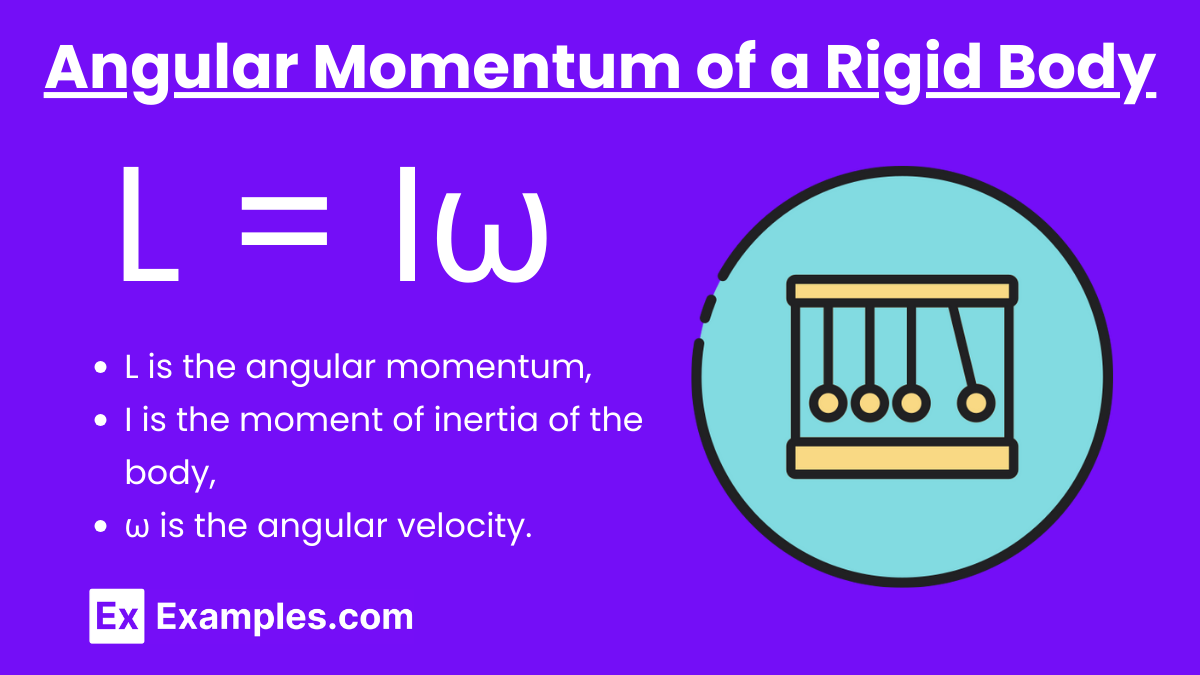
Formula: L = Iω
where:
- L is the angular momentum,
- I is the moment of inertia,
- ω is the angular velocity.
Moment of Inertia
Moment of Inertia (I): Moment of inertia is a scalar quantity that measures the rotational inertia of an object. It depends on the mass distribution of the object relative to the axis of rotation.
Formula: \[ I = \sum m_i r_i^2 \]
where:
- mᵢ is the mass of the i-th particle,
- rᵢ is the distance from the axis of rotation.
Conservation of Angular Momentum
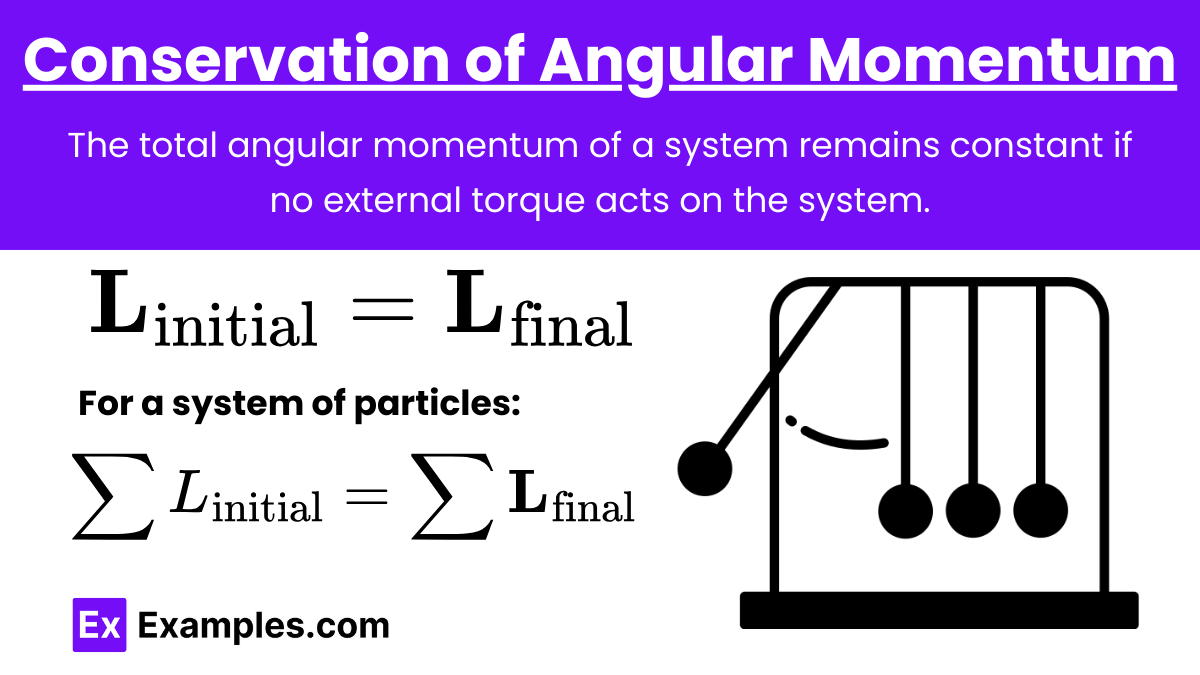
Principle of Conservation of Angular Momentum: The angular momentum of a system remains constant if no external torques act on it.
Formula: \[ \mathbf{L}_{\text{initial}} = \mathbf{L}_{\text{final}} \] \[ I_{\text{initial}}\omega_{\text{initial}} = I_{\text{final}}\omega_{\text{final}} \]
Key Points:
- Angular momentum is conserved in the absence of external torques.
- This principle applies to isolated systems.
Examples
Example 1: Ice Skater
Scenario: An ice skater with arms extended spins at an angular velocity of 2 rad/s. When the skater pulls in their arms, their moment of inertia decreases to half its original value. Find the new angular velocity.
Solution:
Example 2: Rotating Disc
Scenario: A disc of moment of inertia 0.1kg⋅m² rotates at 10 rad/s. A second disc of moment of inertia 0.2kg⋅m² initially at rest is dropped onto the first disc. Find the final angular velocity of the system.
Solution: \[ I_{\text{initial}}\omega_{\text{initial}} = I_{\text{final}}\omega_{\text{final}} \] \[ I_{\text{initial}} \cdot 2 \, \text{rad/s} = \frac{I_{\text{initial}}}{2} \cdot \omega_{\text{final}} \] \[ 2 \, \text{rad/s} = \frac{1}{2} \omega_{\text{final}} \] \[ \omega_{\text{final}} = 4 \, \text{rad/s} \]
Example 3: Planetary Motion
Scenario: A planet orbits a star in an elliptical orbit. At its closest approach (perihelion), the planet’s distance from the star is 1×10¹¹m and its speed is 3×10⁴m/s. At its farthest distance (aphelion), the distance is 2×10¹¹m. Find the speed of the planet at aphelion.
Solution: \[ L_{\text{perihelion}} = L_{\text{aphelion}} \] \[ m r_p v_p = m r_a v_a \] \[ r_p v_p = r_a v_a \] \[ 1 \times 10^{11} \cdot 3 \times 10^{4} = 2 \times 10^{11} \cdot v_a \] \[ v_a = \frac{3 \times 10^{15}}{2 \times 10^{11}} \] \[ v_a = 1.5 \times 10^{4} \, \text{m/s} \]
Example 4: Divers
Scenario: A diver jumps off a diving board with a rotational speed of 1.5 rad/s in a tuck position (moment of inertia 6kg⋅m²). As the diver extends into a straight position, their moment of inertia increases to 12kg⋅m². Find the new rotational speed.
Solution: \[ L_{\text{initial}} = L_{\text{final}} \] \[ I_{\text{tuck}} \omega_{\text{tuck}} = I_{\text{straight}} \omega_{\text{straight}} \] \[ 6 \cdot 1.5 = 12 \cdot \omega_{\text{straight}} \] \[ 9 = 12 \cdot \omega_{\text{straight}} \] \[ \omega_{\text{straight}} = \frac{9}{12} \] \[ \omega_{\text{straight}} = 0.75 \, \text{rad/s} \]
Example 5: Spinning Figure Skater
Scenario: A figure skater is spinning with her arms extended. Her moment of inertia in this position is 4kg⋅m² and her angular velocity is 2rad/s. She then pulls her arms in, reducing her moment of inertia to 2kg⋅m². Find her new angular velocity.
Solution: \[ I_{\text{initial}} \omega_{\text{initial}} = I_{\text{final}} \omega_{\text{final}} \] \[ 4 \cdot 2 = 2 \cdot \omega_{\text{final}} \] \[ 8 = 2 \cdot \omega_{\text{final}} \] \[ \omega_{\text{final}} = \frac{8}{2} \] \[ \omega_{\text{final}} = 4 \, \text{rad/s} \]
Practice Problems
Question 1:
A figure skater is spinning with her arms extended. When she pulls her arms in close to her body, what happens to her angular velocity?
A) It decreases.
B) It increases.
C) It remains the same.
D) It fluctuates.
Answer: B) It increases.
Explanation:
According to the conservation of angular momentum, the total angular momentum L of the skater remains constant if no external torques act on her. Angular momentum is given by:
L = Iω
where I is the moment of inertia and ω is the angular velocity. When the skater pulls her arms in, her moment of inertia I decreases. To conserve angular momentum L, her angular velocity ω must increase. Hence, the correct answer is that her angular velocity increases.
Question 2:
A disk with moment of inertia I and angular velocity ω collides with a second identical disk initially at rest. If they stick together after the collision, what is the final angular velocity of the system?
\[ \text{A) } \frac{\omega}{4} \] \[ \text{B) } \frac{3\omega}{2} \] \[ \text{C) } \omega \] \[ \text{D) } 2\omega \] \[ \text{Answer: B) } \frac{3\omega}{2} \]
Explanation:
Before the collision, the total angular momentum of the system is:
Lᵢₙᵢₜᵢₐₗ = Iω
After the collision, the two disks stick together, and the combined moment of inertia is:
Iբᵢₙₐₗ = 2I
Let ωfinal be the final angular velocity. According to the conservation of angular momentum:
Lᵢₙᵢₜᵢₐₗ = Lբᵢₙₐₗ
Iω = (2I)ω
Solving for ωբᵢₙₐₗ:
\[ \omega_{\text{final}} = \frac{I \omega}{2I} = \frac{\omega}{2} \] \[\text{Thus, the correct answer is } \frac{\omega}{2}. \]
Question 3:
A planet orbits the sun in an elliptical path. When the planet is closest to the sun (at perihelion), its orbital speed is 30 km/s. What happens to its orbital speed when it is farthest from the sun (at aphelion)?
A) It decreases.
B) It increases.
C) It remains the same.
D) It fluctuates randomly.
Answer: A) It decreases.
Explanation:
The conservation of angular momentum applies to the planet’s orbit around the sun. At perihelion (closest approach), the planet has a smaller orbital radius r and a higher speed v. At aphelion (farthest distance), the orbital radius r is larger, and to conserve angular momentum, the speed v must decrease.
Angular momentum L is given by:
L = mrv
where m is the mass of the planet, r is the distance from the sun, and v is the orbital speed. Since L is conserved:
\[ m r_{\text{perihelion}} v_{\text{periheli}} = m r_{\text{aphelion}} v_{\text{aphelion}} \] \[ r_{\text{periheli}} v_{\text{periheli}} = r_{\text{aphelion}} v_{\text{aphelion}} \]
Given that rₐₚₕₑₗᵢₒₙ>rₚₑᵣᵢₕₑₗᵢₒₙ, it follows that vₐₚₕₑₗᵢₒₙ<vₚₑᵣᵢₕₑₗᵢₒₙ. Therefore, the planet’s orbital speed decreases at aphelion. Hence, the correct answer is that the orbital speed decreases.