Conservation of Energy, the Work–Energy Principle, and Power

Understanding the principles of energy conservation, the work-energy principle, and power is essential for mastering the concepts of mechanics and achieving a high score on the AP Physics exam. These principles are fundamental to analyzing the behavior of objects in various physical scenarios. Below are detailed notes to help you excel in this topic.

Free AP Physics 1: Algebra-Based Practice Test

Learning Objectives

In the AP Physics exam, students should understand the principles of Conservation of Energy, the Work–Energy Principle, and Power. This includes comprehending how energy is conserved in isolated systems, applying the work-energy theorem to solve problems, and calculating power as the rate of energy transfer. Additionally, students should be able to analyze real-world scenarios using these concepts, perform calculations involving kinetic and potential energy, and understand the implications of energy transformations and efficiency in physical systems.

Conservation of Energy

Definition: The law of conservation of energy states that the total energy of an isolated system remains constant over time. Energy can neither be created nor destroyed, but it can be transformed from one form to another.

Types of Energy

1. Kinetic Energy (K):

   • Energy associated with the motion of an object.

   • Formula: K = \frac{1}{2}mv^2

2. Potential Energy (U):

   • Energy associated with the position or configuration of an object.

   • Gravitational Potential Energy (Ug​):

   • Formula: Ug = mgh

   • m is the mass

   • g is the acceleration due to gravity

   • h is the height above a reference point

   • Elastic Potential Energy (Uₑ​):

   • Formula: U_e = \frac{1}{2}kx^2

3. Mechanical Energy (E):

   • The sum of kinetic and potential energy in a system.

   • Formula: E = K+U

Examples

1. Pendulum: As a pendulum swings, potential energy at the highest points converts to kinetic energy at the lowest point and vice versa, with total mechanical energy remaining constant.

2. Roller Coaster: The total energy of the coaster (kinetic + potential) remains constant, neglecting friction and air resistance.

Conservation of Mechanical Energy

Principle: In the absence of non-conservative force (e.g., friction, air resistance), the total mechanical energy of a system remains constant.

Equation: E_{\text{initial}} = E_{\text{final}} K_i + U_i = K_f + U_f

Examples

1. Pendulum:

   • At the highest point: E = U

   • At the lowest point: E = K

2. Roller Coaster:

   • At the top of a hill: E = U

   • At the bottom of a hill: E = K

The Work–Energy Principle

Definition: The work-energy principle states that the work done on an object is equal to the change in its kinetic energy.

Formula: W = \Delta K
W = K_f - K_i

Work

Definition: Work (W) is done when a force (F) causes a displacement (d) of an object in the direction of the force.

Formula: W = Fdcos⁡θ

• F is the magnitude of the force

• d is the displacement

• θ is the angle between the force and displacement vectors

Units: Joules (J)

Examples

1. Lifting an Object:

   • Work done against gravity: W = mgh

2. Spring Compression:

   • Work done on a spring: W = \frac{1}{2} k x^2

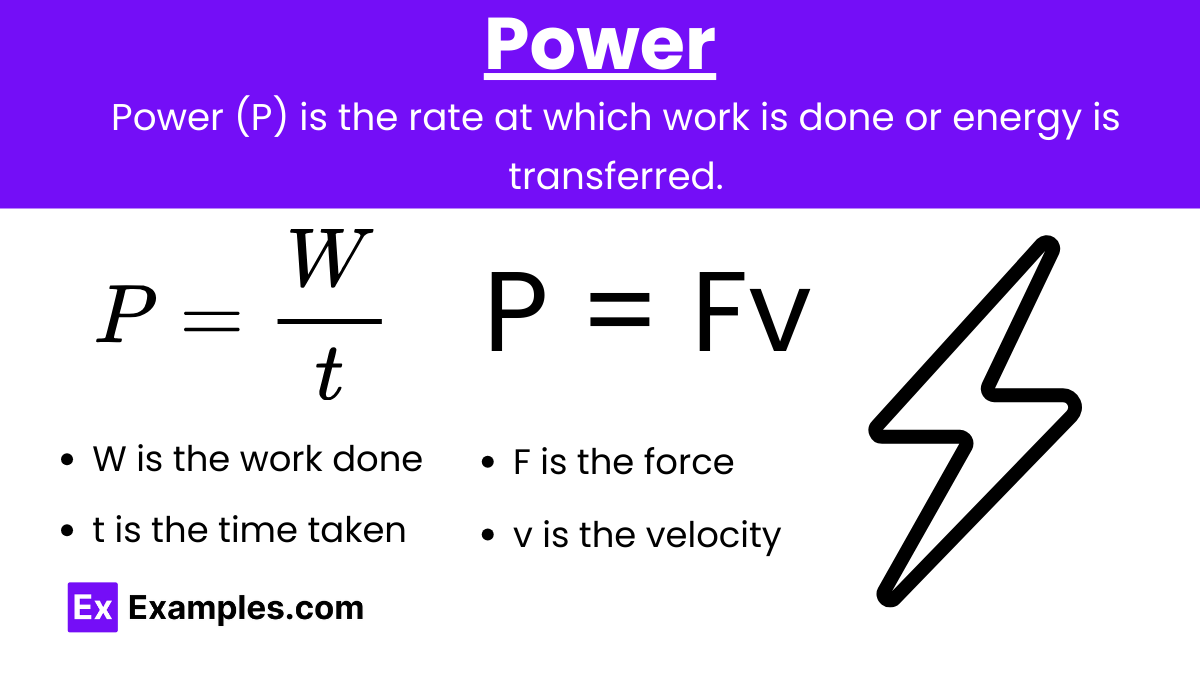
Power

Definition: Power (P) is the rate at which work is done or energy is transferred.

Formula: P = \frac{W}{t}

• W is the work done

• t is the time taken

Alternative Formula: P = Fv

• F is the force

• v is the velocity

Units: Watts (W), where 1 W = 1 J/s

Examples

1. Climbing Stairs:

   • Power output: P = \frac{mgh}{t}

2. Electric Motor:

   • Power output: P = IV

   • I is the current

   • V is the voltage

Problems

Example 1: Conservation of Energy in a Pendulum

Scenario: A pendulum bob of mass 2 kg is raised to a height of 1.5 meters. Calculate its speed at the lowest point.

Solution: E_{\text{initial}} = U_i = mgh = 2 \times 9.8 \times 1.5 = 29.4 \, \text{J} At the lowest point, $E_{\text{final}} = K_f:$$E_{\text{final}} = K_f: $ K_f = \frac{1}{2} mv^2 29.4 = \frac{1}{2} \times 2 \times v^2 v^2 = \frac{29.4}{1} v = \sqrt{29.4} \approx 5.42 \, \text{m/s}

Example 2: Work-Energy Principle in a Car

Scenario: A car of mass 1000 kg accelerates from 20 m/s to 30 m/s. Calculate the work done by the engine.

Solution: \Delta K = K_f - K_i = \frac{1}{2} mv_f^2 - \frac{1}{2} mv_i^2 \Delta K = \frac{1}{2} \times 1000 \times 30^2 - \frac{1}{2} \times 1000 \times 20^2 \Delta K = 450000 - 200000 = 250000 \, \text{J}

Example 3: Power Output of a Cyclist

Scenario: A cyclist exerts a force of 200 N to move at a constant speed of 5 m/s. Calculate the power output.

Solution: P = Fv = 200×5 = 1000W

Applications

1. Engineering

• Energy Conservation: Designing systems (like buildings or vehicles) to use energy more efficiently by minimizing energy losses.

• Power Plants: Managing the rate of energy transfer to supply electricity effectively.

2. Renewable Energy

• Solar Panels: Converting sunlight into electrical energy, conserving energy, and providing power.

• Wind Turbines: Harnessing wind energy to generate power.

3. Everyday Life

• Household Appliances: Power ratings on appliances help consumers understand energy consumption and efficiency.

• Sports: Athletes use the work-energy principle to improve performance by optimizing their energy use.

4. Transportation

• Fuel Efficiency: Understanding energy conservation helps in designing more fuel-efficient vehicles.

• Electric Vehicles: Power management is crucial for battery life and performance.