Conservation of Linear Momentum

Last Updated: November 7, 2024

Notes

Understanding the conservation of linear momentum is crucial for mastering the principles of mechanics and achieving a high score on the AP Physics exam. This principle applies to isolated systems and is fundamental in analyzing collisions and other interactions between objects. Below are detailed notes to help you excel in this topic.

Free AP Physics 1: Algebra-Based Practice Test

Learning Objectives

For the AP Physics exam, you should understand the principle of conservation of linear momentum, including its mathematical formulation and applications. Learn to analyze and solve problems involving collisions (elastic and inelastic), explosions, and isolated systems. Understand how external and internal force affect momentum, and apply the conservation law to predict outcomes in various physical scenarios. Master the concepts of impulse, momentum changes, and how they relate to Newton’s laws of motion.

Definition of Linear Momentum

Linear Momentum (p): Linear momentum is a vector quantity defined as the product of an object’s mass and its velocity. It is given by:

p = mv

where:

p is the linear momentum,
m is the mass of the object,
v is the velocity of the object.

Key Points:

Linear momentum has both magnitude and direction.
The SI unit of momentum is kilogram meter per second (kg·m/s).

Conservation of Linear Momentum

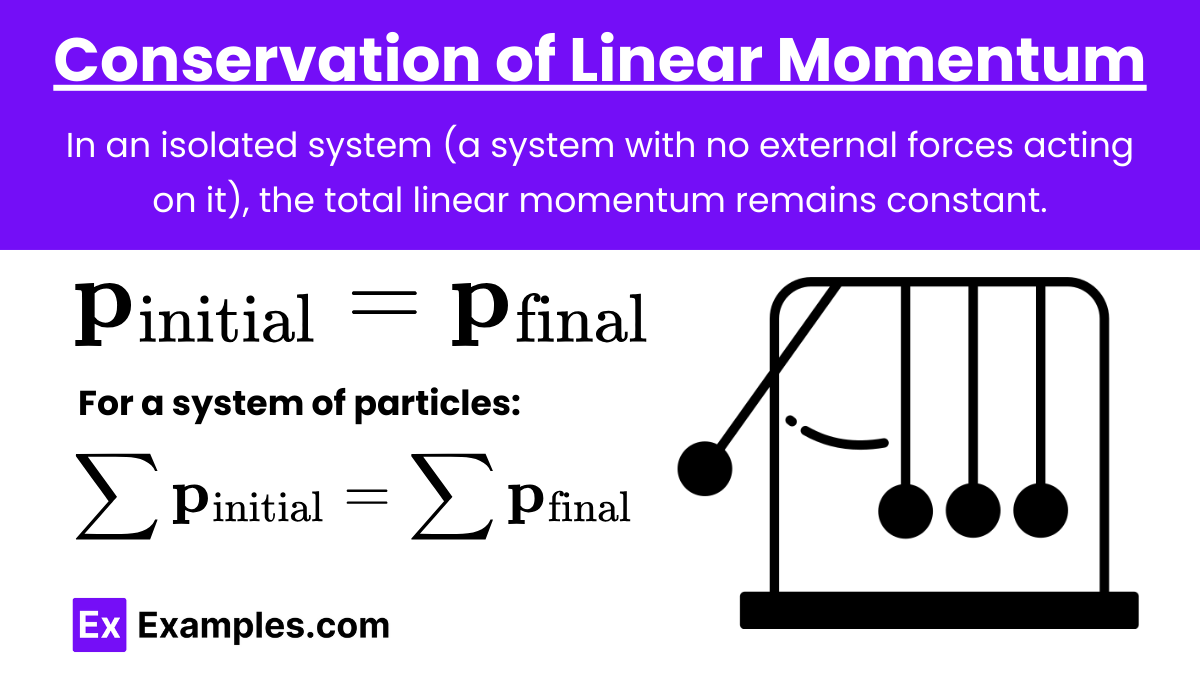
Principle of Conservation of Linear Momentum: In an isolated system (a system with no external forces acting on it), the total linear momentum remains constant. This means that the total momentum before an interaction is equal to the total momentum after the interaction.

Mathematically:

$\mathbf{p}_{\text{initial}} = \mathbf{p}_{\text{final}}$

For a system of particles:

$\sum \mathbf{p}_{\text{initial}} = \sum \mathbf{p}_{\text{final}}$

Key Points:

Applies to both elastic and inelastic collisions.
In isolated systems, external forces are absent or negligible.

Types of Collisions

Elastic Collisions

Elastic Collision: A collision in which both momentum and kinetic energy are conserved.

Key Points:

No permanent deformation or generation of heat.
Both momentum and kinetic energy before and after the collision are equal.

Equations:

Conservation of Momentum:
$m_1 v_1 + m_2 v_2 = m_1 v_1' + m_2 v_2'$
Conservation of Kinetic Energy:
$\frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} m_1 v_1'^2 + \frac{1}{2} m_2 v_2'^2$

Inelastic Collisions

Inelastic Collision: A collision in which momentum is conserved, but kinetic energy is not. Some kinetic energy is converted into other forms of energy, such as heat or deformation.

Key Points:

Objects may stick together after collision (perfectly inelastic collision).
Momentum is conserved, but kinetic energy is not.

Equations:

Conservation of Momentum:
$m_1 v_1 + m_2 v_2 = (m_1 + m_2) v'$
(for perfectly inelastic collisions)

Impulse and Momentum

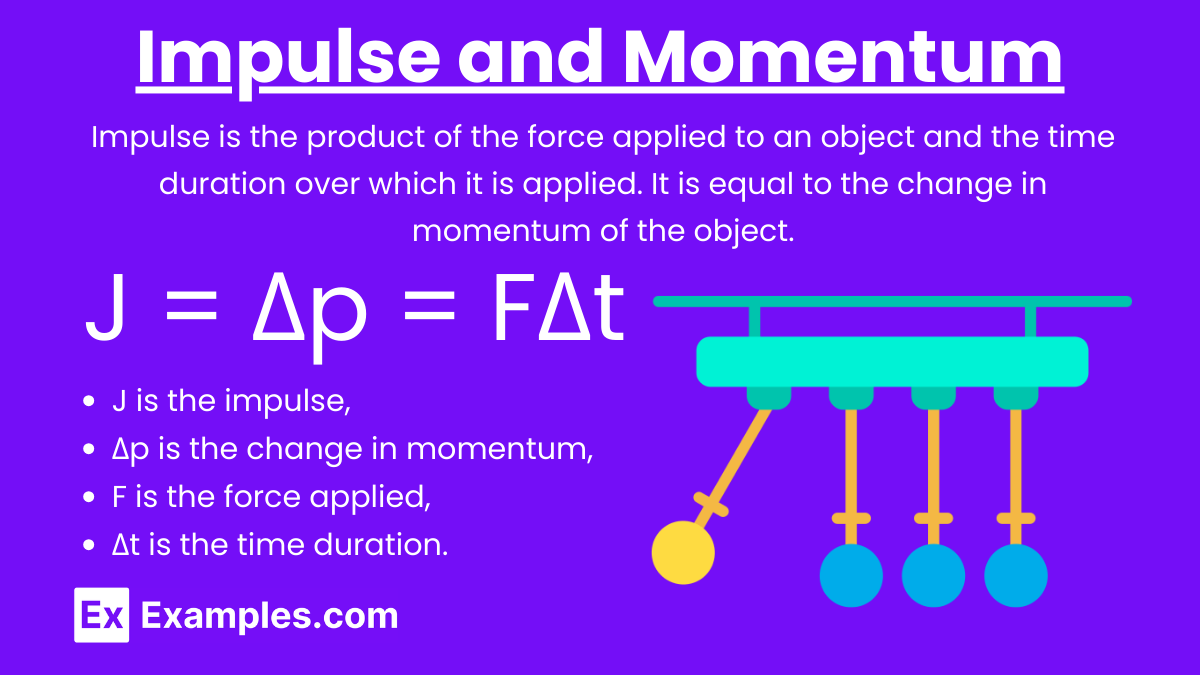
Impulse (J): Impulse is the product of the force applied to an object and the time duration over which it is applied. It is equal to the change in momentum of the object.

Formula: J = Δp = FΔt

where:

J is the impulse,
Δp is the change in momentum,
F is the force applied,
Δt is the time duration.

Key Points:

Impulse has the same units as momentum (N·s or kg·m/s).
Impulse can be represented graphically as the area under a force-time graph.

Examples

Example 1: Elastic Collision

Scenario: Two carts on a frictionless track collide elastically. Cart A has a mass of 2 kg and an initial velocity of 3 m/s. Cart B has a mass of 3 kg and is initially at rest. Calculate their velocities after the collision.

Solution:

Conservation of Momentum:
$m_1 v_{1i} + m_2 v_{2i} = m_1 v_{1f} + m_2 v_{2f}$

$2 \times 3 + 3 \times 0 = 2v_{1f} + 3v_{2f}$

$6 = 2v_{1f} + 3v_{2f}$
Conservation of Kinetic Energy:
$\frac{1}{2} m_1 v_{1i}^2 + \frac{1}{2} m_2 v_{2i}^2 = \frac{1}{2} m_1 v_{1f}^2 + \frac{1}{2} m_2 v_{2f}^2$

$\frac{1}{2} \times 2 \times 3^2 + 0 = \frac{1}{2} \times 2 \times v_{1f}^2 + \frac{1}{2} \times 3 \times v_{2f}^2$

$9 = v_{1f}^2 + 1.5 v_{2f}^2$

Solve the system of equations to find v₁բ and v₂բ.

Example 2: Inelastic Collision

Scenario: A 5 kg object moving at 4 m/s collides inelastically with a 3 kg object initially at rest. They stick together after the collision. Calculate their final velocity.

Solution:

Conservation of Momentum:
$m_1 v_{1i} + m_2 v_{2i} = (m_1 + m_2) v_f$

$5 \times 4 + 3 \times 0 = (5 + 3) v_f$

$20 = 8 v_f$

$v_f = 2.5 \, \text{m/s}$

Example 3: Impulse

Scenario: A 2 kg ball initially moving at 5 m/s is struck by a bat, changing its velocity to -3 m/s in 0.2 seconds. Calculate the impulse and the average force exerted by the bat.

Solution:

Change in Momentum: Δp = mΔv = 2×(−3−5) = −16kg⋅m/s
Impulse: J = Δp = −16N⋅s
Average Force:
$\mathbf{F} = \frac{\mathbf{J}}{\Delta t} = \frac{-16}{0.2} = -80 \, \text{N}$