Energy of a Simple Harmonic Oscillator
Understanding the energy of a simple harmonic oscillator (SHO) is crucial for mastering the concepts of oscillatory motion and energy conservation, which are essential for the AP Physics exam. A simple harmonic oscillator is a system where the restoring force is directly proportional to the displacement and acts in the opposite direction. Below are detailed notes to help you achieve a high score on your AP Physics exam.
Learning Objectives
By studying the energy of a simple harmonic oscillator, you will learn to analyze the potential and kinetic energy interchange in oscillatory motion, calculate the total mechanical energy, and understand energy conservation in the system. You will also gain the ability to use mathematical equations to describe the energy relationships, interpret energy graphs, and apply these concepts to real-world oscillating systems. Mastery of these objectives will prepare you for related questions on the AP Physics exam.
Simple Harmonic Oscillator (SHO)
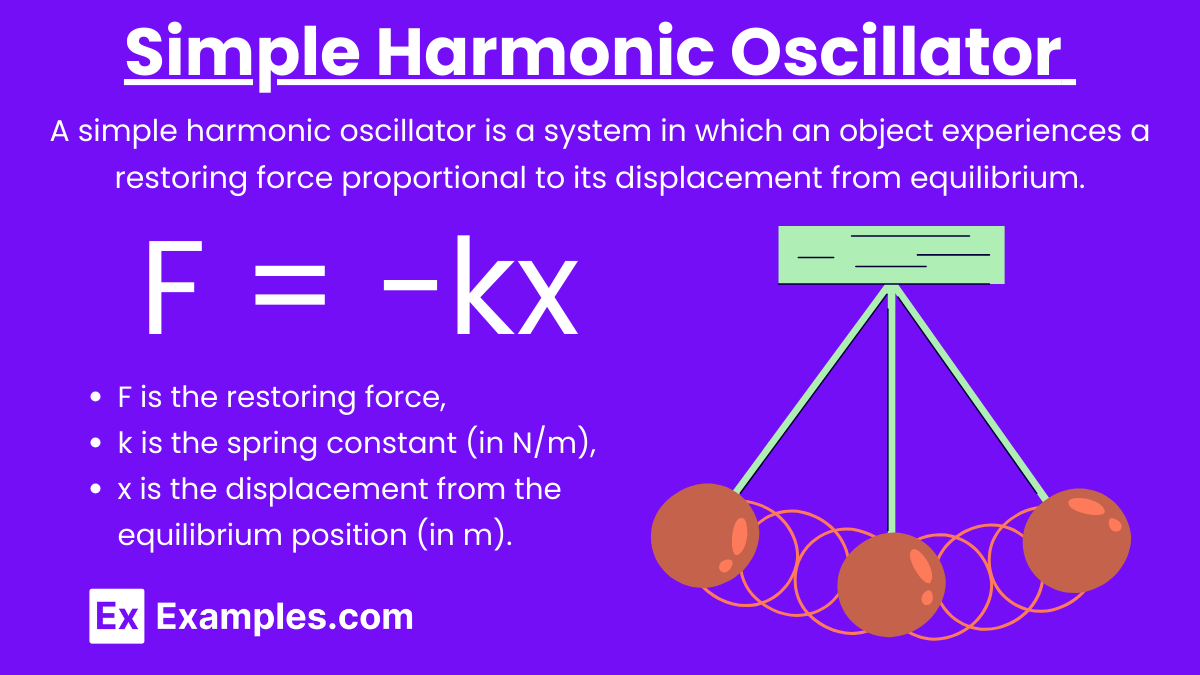
Simple Harmonic Oscillator: A simple harmonic oscillator is a system in which an object experiences a restoring force proportional to its displacement from equilibrium. This force follows Hooke’s Law:
F = −kx
where:
- F is the restoring force,
- k is the spring constant (in N/m),
- x is the displacement from the equilibrium position (in m).
Characteristics
- Period (T): The time taken for one complete cycle of oscillation. \[ T = 2\pi \sqrt{\frac{m}{k}} \]
- Frequency (f): The number of cycles per unit time. \[ f = \frac{1}{T} = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \]
- Angular Frequency (ω): The rate of change of the phase of the oscillation. \[ \omega = 2\pi f = \sqrt{\frac{k}{m}} \]
Energy in a Simple Harmonic Oscillator
Total Mechanical Energy
The total mechanical energy (E) in a simple harmonic oscillator is the sum of its kinetic energy (KE) and potential energy (PE). For a simple harmonic oscillator, the total mechanical energy is constant and is given by:
E = KE+PE
Potential Energy (PE)
The potential energy stored in a spring (or any system exhibiting SHM) is given by:
\[ PE = \frac{1}{2}kx^2 \]
where:
- PE is the potential energy,
- k is the spring constant,
- x is the displacement from the equilibrium position.
Kinetic Energy (KE)
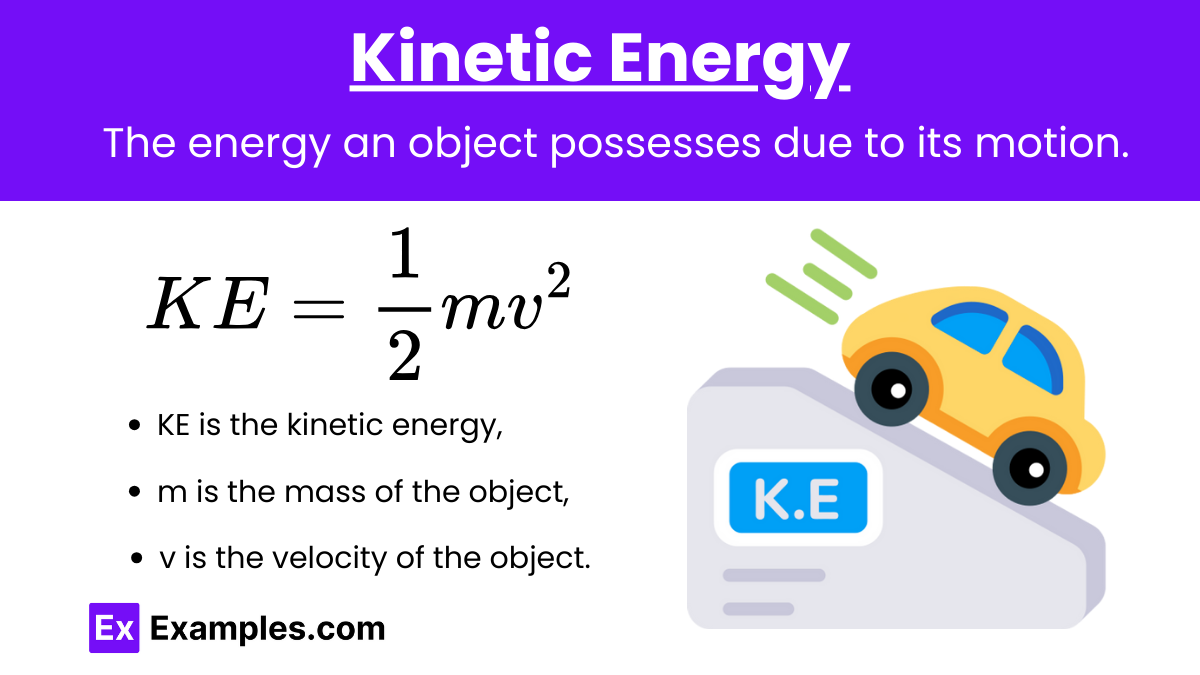
The kinetic energy of a mass in SHM is given by:
\[ KE = \frac{1}{2}mv^2 \]
where:
- KE is the kinetic energy,
- m is the mass,
- v is the velocity.
Velocity in SHM
The velocity of an object in SHM as a function of displacement is given by:
\[ v = \pm \sqrt{\frac{k}{m}(A^2 – x^2)} \]
where:
- A is the amplitude of the oscillation,
- x is the displacement from equilibrium.
Energy Distribution
At any point during the oscillation, the total energy E can be expressed as the sum of kinetic and potential energies. At the equilibrium position (x = 0), all the energy is kinetic:
\[ E = KE_{\text{max}} = \frac{1}{2}kA^2 \]
At the maximum displacement (x = ±Ax), all the energy is potential:
\[ E = PE_{\text{max}} = \frac{1}{2}kA^2 \]
Energy Conservation
The principle of energy conservation in SHM states that the total mechanical energy (sum of kinetic and potential energies) remains constant throughout the motion, assuming no damping forces are present.
\[ \frac{1}{2}kA^2 = \frac{1}{2}kx^2 + \frac{1}{2}mv^2 \]
Example Problems
Example 1: Maximum Speed in SHM
Problem: A mass of 0.5 kg attached to a spring with a spring constant of 200 N/m oscillates with an amplitude of 0.1 m. Calculate the maximum speed of the mass.
Solution: \[ v_{\text{max}} = A \sqrt{\frac{k}{m}} \] \[ v_{\text{max}} = 0.1 \times \sqrt{\frac{200}{0.5}} \] \[ v_{\text{max}} = 0.1 \times \sqrt{400} \] \[ v_{\text{max}} = 0.1 \times 20 \] \[ v_{\text{max}} = 2 \, \text{m/s} \]
Example 2: Energy Distribution at a Given Displacement
Problem: A 1 kg mass attached to a spring with a spring constant of 100 N/m oscillates with an amplitude of 0.2 m. Calculate the kinetic and potential energies when the mass is 0.1 m from the equilibrium position.
Solution: Total energy: \[ E = \frac{1}{2} k A^2 = \frac{1}{2} \times 100 \times 0.2^2 = 2 \, \text{J} \]
Potential energy at x=0.1 m: \[ PE = \frac{1}{2} k x^2 = \frac{1}{2} \times 100 \times 0.1^2 = 0.5 \, \text{J} \]
Kinetic energy: KE = E−PE = 2−0.5 = 1.5J
Example 3: Period of Oscillation
Problem: A mass of 2 kg is attached to a spring with a spring constant of 50 N/m. Calculate the period of oscillation.
Solution: \[ T = 2 \pi \sqrt{\frac{m}{k}} \] \[ T = 2 \pi \sqrt{\frac{2}{50}} \] \[ T = 2 \pi \sqrt{0.04} \] \[ T = 2 \pi \times 0.2 \] \[ T = 0.4 \pi \] \[ T \approx 1.26 \, \text{s} \]
Example 4: Energy Conversion in a Spring-Mass System
Scenario: A spring-mass system with mass 0.2 kg and spring constant 50 N/m is compressed by 0.05 m from its equilibrium position. Calculate the potential energy stored in the spring and the speed of the mass when it passes through the equilibrium position.
Solution:
- Potential Energy (U): \[ U = \frac{1}{2} k x^2 = \frac{1}{2} \times 50 \, \text{N/m} \times (0.05 \, \text{m})^2 = 0.0625 \, \text{J} \]
- Kinetic Energy (K) at equilibrium (equals potential energy at maximum displacement):K = U = 0.0625J
- Speed (v) at equilibrium:\[ K = \frac{1}{2} mv^2 \implies v = \sqrt{\frac{2K}{m}} = \sqrt{\frac{2 \times 0.0625 \, \text{J}}{0.2 \, \text{kg}}} = 0.79 \, \text{m/s} \]
Example 5: Simple Pendulum
Scenario: A simple pendulum with a length of 2 m and a bob of mass 1 kg is displaced to make a maximum angle of 5 degrees with the vertical. Calculate the maximum potential energy.
Solution:
- Maximum Height (h):h ≈ L(1−cosθ) ≈ 2m×(1−cos5⁰) ≈ 2m×0.0038 = 0.0076m
- Maximum Potential Energy (Umax):Uₘₐₓ = mgh = 1kg×9.8m/s²×0.0076m = 0.0745J
Practice Problems
Question 1
Which of the following statements correctly describes the total energy of a simple harmonic oscillator?
a) It is constant and depends on the amplitude of oscillation.
b) It varies with the displacement from the equilibrium position.
c) It is zero at the maximum displacement.
d) It depends on the mass but not on the amplitude.
Answer: a) It is constant and depends on the amplitude of oscillation.
Explanation: The total energy of a simple harmonic oscillator is the sum of its kinetic and potential energy. It remains constant throughout the motion and is given by \[ E = \frac{1}{2} k A^2 \], where k is the spring constant and A is the amplitude of oscillation. The energy does not depend on the position within the cycle but solely on the amplitude.
Question 2
At what point in its motion does a simple harmonic oscillator have maximum kinetic energy?
a) At the maximum displacement.
b) At the equilibrium position.
c) At half the maximum displacement.
d) It is the same at all points.
Answer: b) At the equilibrium position.
Explanation: The kinetic energy of a simple harmonic oscillator is given by \[ E = \frac{1}{2} m v^2 \]. The velocity is maximum when the displacement is zero (i.e., at the equilibrium position). Therefore, the kinetic energy is maximum at the equilibrium position where the oscillator passes through the midpoint of its motion.
Question 3
Which of the following expressions represents the potential energy of a simple harmonic oscillator as a function of displacement x?
\[ a) \quad PE = \frac{1}{2} m \omega^2 x^2 \] \[ b) \quad PE = \frac{1}{2} k x^2 \] \[ c) \quad PE = m g h \] \[ d) \quad PE = \frac{1}{2} k A^2 \] \[ \text{Answer: b)} \quad PE = \frac{1}{2} k x^2 \]
Explanation: The potential energy in a simple harmonic oscillator is stored in the spring (or the restoring force) and is given by \[P E = \frac{1}{2} k x^2 \], where k is the spring constant and x is the displacement from the equilibrium position. This expression shows that the potential energy is directly proportional to the square of the displacement.