Momentum and Impulse

Last Updated: November 7, 2024

Notes

Understanding momentum and impulse is crucial for mastering the principles of dynamics and achieving a high score on the AP Physics exam. These concepts are fundamental in analyzing motion and collisions. Below are detailed notes to help you excel in this topic.

Free AP Physics 1: Algebra-Based Practice Test

Learning Objectives

In this topic, you will learn to define and calculate momentum and impulse, understand their vector nature, and explore their relationship through the impulse-momentum theorem. You will analyze collisions using conservation of momentum, distinguish between elastic and inelastic collisions, and solve problems involving variable forces and time. Additionally, you will interpret and create graphs of force versus time, and apply these concepts to real-world scenarios, ensuring a comprehensive understanding for the AP Physics exam.

Momentum

Momentum (p): Momentum is the product of an object’s mass and its velocity. It is a vector quantity, meaning it has both magnitude and direction.

Formula: p = mv

where:

p is the momentum,
m is the mass of the object,
v is the velocity of the object.

Key Points

Vector Nature: Momentum has both magnitude and direction.
Conservation of Momentum: In a closed system with no external forces, the total momentum before and after an event (e.g., a collision) remains constant.

Characteristics

Vector Quantity: Momentum has both magnitude and direction.
Conservation: In an isolated system, the total momentum remains constant.
Units: The SI unit of momentum is kilogram meter per second (kg·m/s).

Impulse

Impulse (J): Impulse is the change in momentum of an object when a force is applied over a period of time. It is also a vector quantity.

Formula: J = Δp = FΔt

where:

J is the impulse,
Δp is the change in momentum,
F is the average force applied,
Δt is the time duration over which the force is applied.

Key Points

Impulse-Momentum Theorem: The impulse applied to an object is equal to the change in its momentum.
Vector Nature: Impulse has both magnitude and direction, same as the change in momentum.

Characteristics

Vector Quantity: Impulse has both magnitude and direction.
Units: The SI unit of impulse is Newton second (N·s), which is equivalent to kg·m/s.

Representations of Changes in Momentum

Graphical Representation

Force-Time Graphs:

The area under a force-time graph represents the impulse.
This area is equal to the change in momentum.

Change in Momentum: Δp = mΔv

where:

Δp is the change in momentum,
m is the mass,
Δv is the change in velocity.

Impulse-Momentum Theorem: J = FΔt = Δp

Conceptual Representation

Impulse in Collisions:

During collisions, forces act over short time intervals to change the momentum of the objects involved.
The duration and magnitude of the force determine the impulse and consequently the change in momentum.

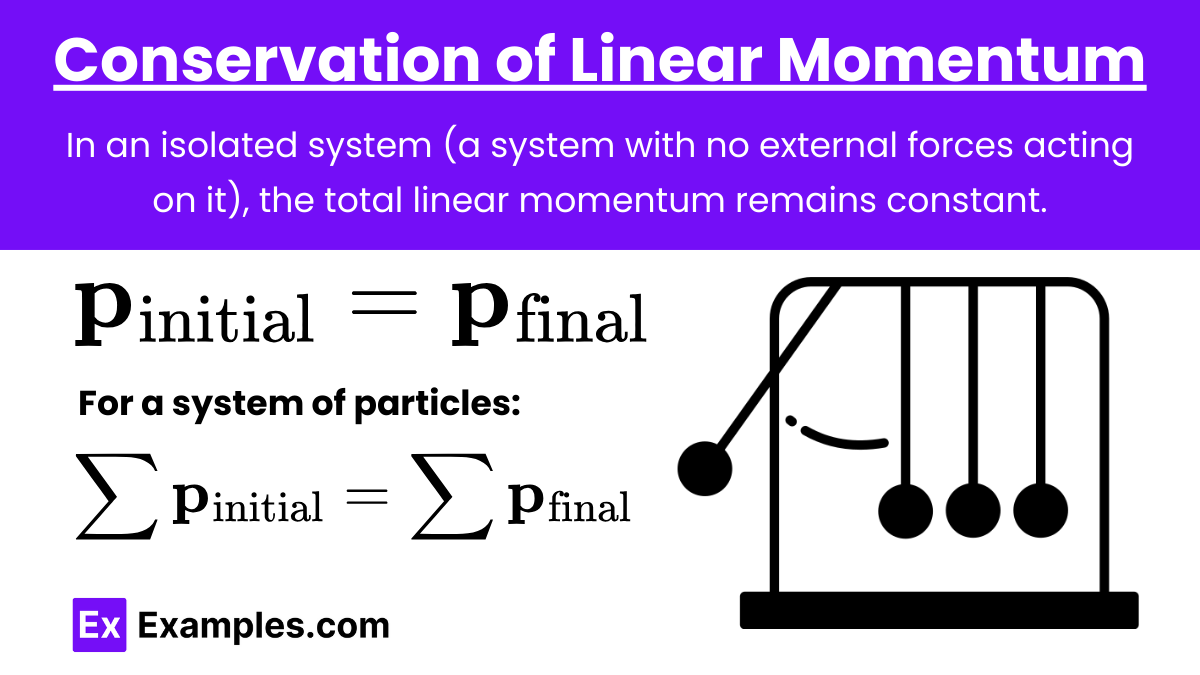
Conservation of Momentum

Principle

Conservation of Momentum: In a closed and isolated system, the total momentum remains constant if no external forces act on the system.

Formula

Total Momentum Before and After Collision:

$\mathbf{P}_{\text{total, before}} = \mathbf{P}_{\text{total, after}}$

where:

$\mathbf{P}_{\text{total, before}}$

is the total momentum before the event,

$\mathbf{P}_{\text{total, after}}$

, after is the total momentum after the event.

Applications and Examples

Example 1: Calculating Momentum

Scenario: A 5 kg ball is moving with a velocity of 3 m/s. Calculate its momentum.

Solution: p = mv
p = 5kg×3m/s
p = 15kg⋅m/s

Example 2: Calculating Impulse

Scenario: A force of 10 N is applied to a 2 kg object for 4 seconds. Calculate the impulse and the change in momentum.

Solution: J = FΔt
J = 10N×4s
J = 40N⋅s

Since impulse equals the change in momentum: Δp = J = 40N⋅s

Example 3: Conservation of Momentum in a Collision

Scenario: Two ice skaters, one with mass 50 kg moving at 2 m/s and the other with mass 70 kg initially at rest, collide and stick together. Calculate their final velocity.

Solution:

$\mathbf{P}_{\text{initial}} = m_1 v_1 + m_2 v_2$

$\mathbf{P}_{\text{initial}} = 50\, \text{kg} \times 2\, \text{m/s} + 70\, \text{kg} \times 0\, \text{m/s}$

$\mathbf{P}_{\text{initial}} = 100\, \text{kg} \cdot \text{m/s}$

Let vբ be their final velocity:

$\mathbf{P}_{\text{final}} = (m_1 + m_2) \mathbf{v}_f$

$100\, \text{kg} \cdot \text{m/s} = (50\, \text{kg} + 70\, \text{kg}) \mathbf{v}_f$

$100\, \text{kg} \cdot \text{m/s} = 120\, \text{kg} \mathbf{v}_f$

$\mathbf{v}_f = \frac{100\, \text{kg} \cdot \text{m/s}}{120\, \text{kg}}$

$\mathbf{v}_f \approx 0.83\, \text{m/s}$

Example 4: Force-Time Graph

Scenario: A force-time graph shows a force applied over a time interval of 5 seconds. The force increases linearly from 0 to 20 N. Calculate the impulse.

Solution: The area under the force-time graph represents the impulse. For a triangle:

$\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$

$\mathbf{J} = \frac{1}{2} \times 5\, \text{s} \times 20\, \text{N}$

$\mathbf{J} = 50\, \text{N} \cdot \text{s}$

Applications

1. Safety Features in Vehicles

Seatbelts and Airbags: Designed to increase the time over which the force from a collision acts, thereby reducing the impulse experienced by passengers and minimizing injuries.
Crumple Zones: Areas in a vehicle designed to deform and absorb energy during a collision, increasing the time over which the collision occurs and reducing the force experienced by passengers.

2. Sports

Football: Players use impulse to change the momentum of the ball when passing, kicking, or tackling.
Tennis: The racket applies an impulse to the ball, changing its momentum and direction.

3. Engineering

Building Structures: Engineers design structures to withstand various forces by considering the impulse and momentum changes during events like earthquakes and high winds.
Manufacturing: Robots and machines use impulse to manipulate objects, ensuring precise control over their motion and positioning.