Systems

Team English - Examples.com
Last Updated: November 7, 2024

Understanding the concept of systems in physics is crucial for mastering the AP Physics exam. This topic involves analyzing how different parts of a physical system interact and how energy and momentum are transferred within and between systems. Below are detailed notes to help you achieve a high score on your AP Physics exam.

Free AP Physics 1: Algebra-Based Practice Test

Learning Objectives

By studying Systems for the AP Physics exam, you should learn to define and differentiate between open, closed, and isolated systems, understand system boundaries, and apply conservation laws of energy and momentum to analyze interactions within and between systems. You should also master drawing and interpreting free-body diagrams, applying Newton’s laws of motion, and solving problems involving system dynamics, such as collisions and energy transfers. These skills will enable you to effectively analyze and solve complex physical scenarios on the exam.

Definition of a System

A system is a collection of objects that interact with each other and can be isolated for study. In physics, systems are defined to analyze the behavior of interacting components and to understand how external forces affect the system.

Types of Systems

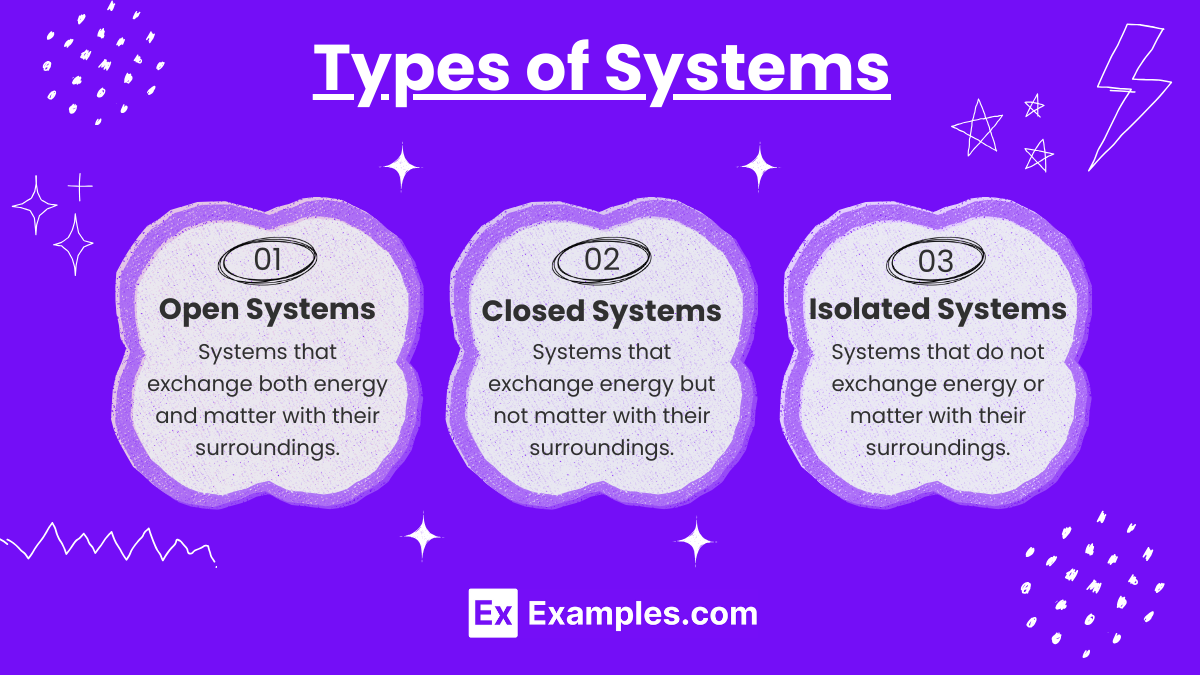
Types of Systems

Open Systems

  • Definition: Systems that exchange both energy and matter with their surroundings.
  • Example: A boiling pot of water. Heat (energy) and steam (matter) are exchanged with the environment.

Closed Systems

  • Definition: Systems that exchange energy but not matter with their surroundings.
  • Example: A sealed thermos bottle. It can exchange heat with the environment but not matter.

Isolated Systems

  • Definition: Systems that do not exchange energy or matter with their surroundings.
  • Example: An insulated cooler (ideally). No heat or matter is exchanged with the environment.

Conservation Laws in Systems

Conservation of Energy

Conservation of Energy

The conservation of energy principle states that the total energy in an isolated system remains constant. Energy can be transferred within the system or across its boundaries but cannot be created or destroyed.

Equation:

    \[ E_{\text{total}} = K + U + E_{\text{int}} \]

Conservation of Momentum

Conservation of Momentum

The conservation of momentum principle states that the total momentum of an isolated system remains constant. Momentum can be transferred within the system, but the total remains unchanged.

Equation:

    \[ \mathbf{p_{\text{total}}} = \mathbf{p_1} + \mathbf{p_2} + \ldots = \text{constant} \]



where K is kinetic energy, U is potential energy, and Eᵢₙₜ is internal energy.

Analyzing Systems

Free-Body Diagrams

Key Points:

  • Free-body diagrams (FBDs) help visualize the forces acting on each component of a system.
  • Each force is represented by an arrow indicating its direction and magnitude.

Steps to Draw FBDs:

  • Identify the object to be analyzed.
  • Draw all external forces acting on the object.
  • Label the forces and indicate their directions.

Newton’s Laws of Motion

Newton's Laws of Motion

Key Points:

  • First Law (Inertia): An object remains at rest or in uniform motion unless acted upon by an external force.
  • Second Law (F = ma): The acceleration of an object is proportional to the net force acting on it and inversely proportional to its mass.
  • Third Law (Action-Reaction): For every action, there is an equal and opposite reaction.

Application:

  • Apply Newton’s laws to each component of the system separately.
  • Use FBDs to identify net forces and solve for unknowns.

Examples

Example 1: Atwood Machine

An Atwood machine consists of two masses connected by a string over a pulley.

System Analysis:

  • Define the system as the two masses and the pulley.
  • Draw FBDs for each mass.
  • Apply Newton’s second law to each mass.
  • Solve the system of equations to find the acceleration and tension in the string.

Example 2: Collisions

Consider a collision between two carts on a frictionless track.

System Analysis:

  • Define the system as both carts.
  • Use conservation of momentum to analyze the collision.
  • If the collision is elastic, also use conservation of kinetic energy.

Equations:

    \[ \mathbf{p_{\text{initial}}} = \mathbf{p_{\text{final}}} \]


where p is momentum

Example 3: Energy Transfer in a Roller Coaster

Analyze a roller coaster as it moves along its track.

System Analysis:

  • Define the system as the roller coaster and track.
  • Use conservation of energy to relate kinetic and potential energy at different points.
  • Account for energy losses due to friction if necessary.

Equation:

    \[ E_{\text{total}} = K + U \]

    \[ K_1 + U_1 = K_2 + U_2 \, \text{(assuming no friction)} \]