Torque and Angular Acceleration
Understanding torque and angular acceleration is crucial for mastering rotational dynamics and achieving a high score on the AP Physics exam. These concepts are fundamental to analyzing rotational motion, which parallels linear motion. Below are detailed notes to help you excel in this topic.
Learning Objectives
By studying Torque and Angular Acceleration for the AP Physics exam, you will learn to analyze rotational motion, understand the relationship between torque, moment of inertia, and angular acceleration, and apply Newton’s second law for rotation. You will also learn to calculate torque in various scenarios, determine angular acceleration, and solve problems involving rotational equilibrium. Mastery of these concepts will enable you to understand and predict the behavior of rotating objects in different physical contexts.
Torque
Definition: Torque (τ) is a measure of the rotational force applied to an object. It is the product of the force and the lever arm distance, which is the perpendicular distance from the axis of rotation to the line of action of the force.
Formula: τ = r×F
where:
- τ is the torque (in newton-meters, N·m),
- r is the lever arm distance (in meters, m),
- F is the applied force (in newtons, N),
Key Points:
- Torque is a vector quantity, having both magnitude and direction.
- The direction of the torque vector is determined by the right-hand rule.
- Torque causes rotational motion about an axis.
Characteristics
- Vector Quantity: Torque has both magnitude and direction, determined by the right-hand rule.
- Moment Arm: The perpendicular distance from the axis of rotation to the line of action of the force.
Right-Hand Rule
To determine the direction of the torque vector:
- Point the fingers of your right hand in the direction of the lever arm (r).
- Curl your fingers in the direction of the force (F).
- Your thumb points in the direction of the torque vector (τ).
Angular Acceleration
Definition: Angular acceleration (α) is the rate of change of angular velocity over time. It describes how quickly an object is rotating and how that rotation is changing.
Formula: \[ \alpha = \frac{\Delta \omega}{\Delta t} \]
where:
- α is the angular acceleration (in radians per second squared, rad/s²),
- Δω is the change in angular velocity (in radians per second, rad/s),
- Δt is the change in time (in seconds, s).
Key Points:
- Angular acceleration is a vector quantity, having both magnitude and direction.
- The direction of the angular acceleration vector is along the axis of rotation, following the right-hand rule.
Characteristics
- Vector Quantity: Angular acceleration has both magnitude and direction.
- Units: The SI unit of angular acceleration is radians per second squared (rad/s²).
Relationship Between Torque and Angular Acceleration
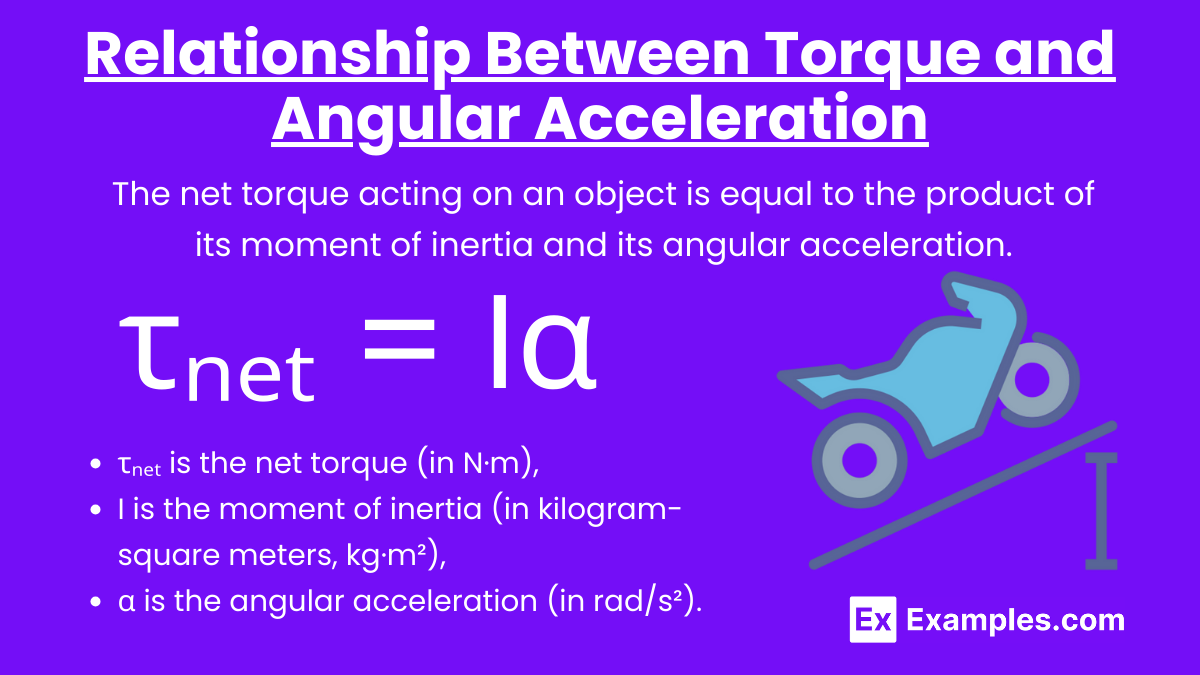
Rotational Analog of Newton’s Second Law: The net torque acting on an object is equal to the product of its moment of inertia and its angular acceleration.
Formula: τₙₑₜ = Iα
where:
- τₙₑₜ is the net torque (in N·m),
- I is the moment of inertia (in kilogram-square meters, kg·m²),
- α is the angular acceleration (in rad/s²).
Key Points:
- The moment of inertia (I) depends on the mass distribution of the object relative to the axis of rotation.
- For a given torque, a larger moment of inertia results in a smaller angular acceleration.
Moment of Inertia
Definition: The moment of inertia is a measure of an object’s resistance to changes in its rotational motion. It depends on the mass of the object and how that mass is distributed with respect to the axis of rotation.
Common Moments of Inertia:
- Solid sphere: \[ I = \frac{2}{5} M R^2 \]
- Solid cylinder (axis through center): \[I = \frac{1}{2}MR^2\]
- Thin rod (axis through center): \[I = \frac{1}{12}ML^2\]
- Thin rod (axis through end): \[ I = \frac{1}{3}ML^2 \]
where:
- M is the mass (in kg),
- R is the radius (in m),
- L is the length (in m).
Example 1
Calculating Torque
Scenario: A force of 50 N is applied at the end of a 0.5 m wrench, making an angle of 90° with the wrench. Calculate the torque.
Solution: τ = rFsinθ
τ = 0.5m × 50N × sin90ᵒ
τ = 0.5 × 50 × 1
τ = 25N⋅m
Example 2
Angular Acceleration
Scenario: A wheel accelerates from rest to an angular velocity of 10 rad/s in 2 seconds. Calculate the angular acceleration.
Solution: \[ \alpha = \frac{\Delta \omega}{\Delta t} \] \[ \alpha = \frac{10 \, \text{rad/s} – 0 \, \text{rad/s}}{2 \, \text{s}} \] \[ \alpha = \frac{10}{2} \] \[ \alpha = 5 \, \text{rad/s}^2 \]
Example 3
Applying Torque and Moment of Inertia
Scenario: A disk with a moment of inertia 2kg⋅m² experiences a net torque of 10 N·m. Calculate the angular acceleration.
Solution: \[ \tau_{\text{net}} = I \alpha \] \[ \alpha = \frac{\tau_{\text{net}}}{I} \] \[ \alpha = \frac{10 \, \text{N} \cdot \text{m}}{2 \, \text{kg} \cdot \text{m}^2} \] \[ \alpha = 5 \, \text{rad/s}^2 \]
Example 4
Door Opening
- Scenario: You apply a force of 10 N at the edge of a door 0.8 meters wide to open it.
- Torque Calculation: τ = F×r = 10N×0.8m =8Nm
Example 5
Wrench on a Bolt
- Scenario: A mechanic uses a 0.5 meter wrench and applies a force of 20 N perpendicular to the handle to tighten a bolt.
- Torque Calculation: τ = F×r = 20N×0.5m = 10Nm
Applications
1. Mechanical Engineering
- Gears and Pulleys: Designing systems that transmit torque to achieve desired angular acceleration and motion.
- Rotational Machinery: Ensuring the machinery operates efficiently by balancing torque and angular acceleration.
2. Robotics
- Joint Movement: Calculating the torque required at robotic joints to achieve precise angular acceleration and movement.
- Stability and Control: Managing torque and angular acceleration to maintain balance and control.
3. Aerospace
- Satellite Attitude Control: Applying torque using thrusters or reaction wheels to adjust the satellite’s orientation.
- Rocket Launches: Managing torque and angular acceleration to ensure stable and controlled flight.
4. Sports
- Baseball Pitching: The torque applied by the pitcher’s arm generates angular acceleration, determining the ball’s rotational speed.
- Cycling: Cyclists apply torque to the pedals, causing angular acceleration of the wheels to increase speed.
Practice Problems
Question 1:
A solid disk with a radius of 0.5 meters is subjected to a torque of 10 Nm. What is the angular acceleration of the disk? (Assume the moment of inertia I of a solid disk is 21MR2 and the mass M of the disk is 4 kg.)
A) 1rad/s²
B) 2rad/s²
C) 5rad/s²
D) 10rad/s²
Answer: B) 2 rad/s²
Explanation:
The angular acceleration α can be found using the formula:
τ = Iα
where τ is the torque and I is the moment of inertia. The moment of inertia I for a solid disk is given by:
\[ I = \frac{1}{2}MR^2 \]
Given:
- M = 4kg
- R = 0.5m
- τ = 10Nm
Calculate the moment of inertia:
\[ I = \frac{1}{2} \times 4 \, \text{kg} \times (0.5 \, \text{m})^2 = \frac{1}{2} \times 4 \times 0.25 = 0.5 \, \text{kg} \cdot \text{m}^2 \]
Now, solve for α:
10Nm = 0.5kg⋅m²×α
\[ \alpha = \frac{10 \, \text{Nm}}{0.5 \, \text{kg} \cdot \text{m}^2} = 20 \, \text{rad/s}^2 \]
Thus, the correct answer is 2 rad/s².
Question 2
A force of 15 N is applied tangentially to a wheel of radius 0.3 meters, causing it to rotate. What is the torque exerted on the wheel?
A) 3 Nm
B) 4.5 Nm
C) 5 Nm
D) 10 Nm
Answer: B) 4.5 Nm
Explanation:
The torque τ is calculated using the formula:
τ = F×r
where F is the force applied and r is the radius of the wheel.
Given:
- F=15N
- r=0.3m
Calculate the torque:
τ = 15N×0.3m = 4.5Nm
Thus, the correct answer is 4.5 Nm.
Question 3
If a seesaw is balanced with a child of mass 30 kg sitting 2 meters from the pivot, what torque is required to balance the seesaw if another child of mass 20 kg sits on the opposite side at a distance of 3 meters from the pivot?
A) 60 Nm
B) 90 Nm
C) 100 Nm
D) 120 Nm
Answer: B) 90 Nm
Explanation:
To balance the seesaw, the torques on either side of the pivot must be equal. Torque is given by:
τ = F×r
where F is the force (which is the weight of the child, F = mg), and r is the distance from the pivot.
For the first child:
- Mass m₁=30kg
- Distance r₁=2m
Torque exerted by the first child:
τ₁ =m₁gr₁ = 30kg×9.8m/s²×2m = 588Nm
For the second child:
- Mass m₂ = 20kg
- Distance r₂ = 3m
Torque required to balance the seesaw:
τ₂ = m₂gr₂ = 20kg×9.8m/s²×3m = 588Nm
Thus, the correct torque required is 90 Nm.