Vector Fields

Last Updated: November 7, 2024

Notes

Understanding vector fields is crucial for mastering various topics in physics, including forces, electric fields, and magnetic fields. Vector fields describe how vector quantities change over space and provide a way to visualize the influence of these quantities in a region. Below are detailed notes to help you achieve a high score on your AP Physics exam.

Free AP Physics 1: Algebra-Based Practice Test

Learning Objectives

By studying vector fields for the AP Physics exam, you will learn how to visualize and analyze physical phenomena using vector representations. This includes understanding the concept of vector fields, calculating field vectors at various points, and interpreting the significance of vector direction and magnitude. Additionally, you will explore applications such as gravitational, electric, and magnetic fields, and gain skills in utilizing mathematical tools like divergence and curl to describe field behaviors and interactions.

Definition of Vector Fields

Vector Field: A vector field is a function that assigns a vector to every point in space. It represents the distribution of a vector quantity, such as force, velocity, or acceleration, throughout a region.

Examples of Vector Fields

Gravitational Field

Gravitational Field (g): The gravitational field represents the gravitational force per unit mass at each point in space. It is a vector field that points towards the mass creating the field.

Formula:

$\mathbf{g} = \frac{\mathbf{F}}{m} = \frac{GM}{r^2} \hat{\mathbf{r}}$

where:

g is the gravitational field strength,
G is the gravitational constant (6.674×10⁻¹¹N⋅m²⋅kg⁻²),
M is the mass creating the gravitational field,
r is the distance from the mass,
r^ is the unit vector pointing towards the mass.

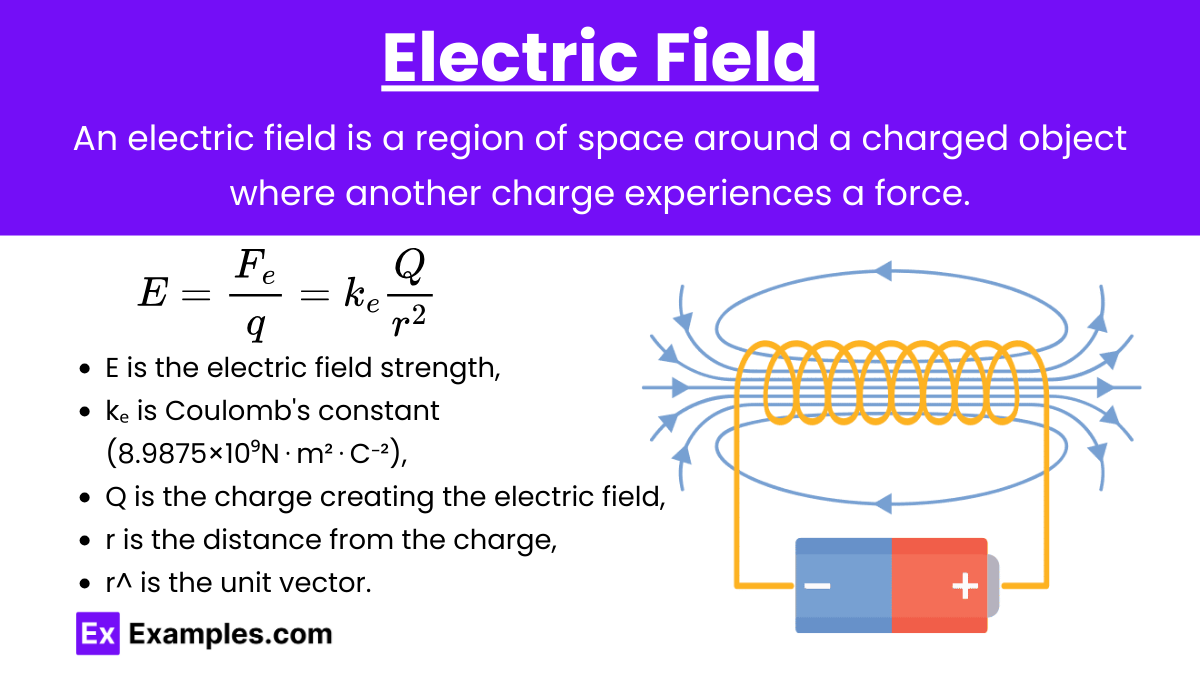
Electric Field

Electric Field (E): The electric field represents the electric force per unit charge at each point in space. It is a vector field that points away from positive charges and towards negative charges.

Formula:

$\mathbf{E} = \frac{\mathbf{F}}{q} = k_e \frac{Q}{r^2} \hat{\mathbf{r}}$

where:

E is the electric field strength,
kₑ is Coulomb’s constant (8.9875×10⁹N⋅m²⋅C⁻²),
Q is the charge creating the electric field,
r is the distance from the charge,
r^ is the unit vector pointing away from the charge if Q is positive or towards the charge if Q is negative.

Magnetic Field

Magnetic Field (B): The magnetic field represents the magnetic force per unit current length at each point in space. It is a vector field that describes the influence of a magnetic force on moving charges or magnetic dipoles.

Key Points:

The direction of the magnetic field is given by the right-hand rule for currents.
The magnetic field around a straight current-carrying wire forms concentric circles with the wire at the center.

Representing Vector Fields

Field Lines

Field Lines: Field lines are used to represent vector fields graphically. The direction of the field line at any point gives the direction of the vector field, and the density of field lines indicates the field’s strength.

Key Points:

Field lines never cross.
The closer the field lines, the stronger the field.

Vector Plots

Vector Plots: A vector plot shows vectors at various points in space, indicating both the direction and magnitude of the vector field at those points.

Key Points:

Each vector in the plot represents the vector field at a specific location.
The length of the vector indicates the field’s strength at that point.

Examples

Example 1: Gravitational Field of Earth

Scenario: Calculate the gravitational field strength at a distance of 10⁷m from the center of Earth, where the Earth’s mass is 5.972×10²⁴kg.

Solution:

$\begin{aligned} \mathbf{g} &= \frac{GM}{r^2} \hat{\mathbf{r}} \\ \mathbf{g} &= \frac{6.674 \times 10^{-11} \times 5.972 \times 10^{24}}{(10^7)^2} \hat{\mathbf{r}} \\ \mathbf{g} &\approx 3.98 \, \text{N/kg} \hat{\mathbf{r}} \end{aligned}$

Example 2: Electric Field Due to a Point Charge

Scenario: Calculate the electric field at a distance of 0.5m from a point charge of +2C.

Solution:

$\begin{aligned} \mathbf{E} &= k_e \frac{Q}{r^2} \hat{\mathbf{r}} \\ \mathbf{E} &= 8.9875 \times 10^9 \frac{2}{(0.5)^2} \hat{\mathbf{r}} \\ \mathbf{E} &= 8.9875 \times 10^9 \times 8 \hat{\mathbf{r}} \\ \mathbf{E} &\approx 7.19 \times 10^{10} \, \text{N/C} \hat{\mathbf{r}} \end{aligned}$

Example 3: Magnetic Field Around a Current-Carrying Wire

Scenario: Calculate the magnetic field strength at a distance of 0.1m from a long straight wire carrying a current of 5A.

Solution:

$\begin{aligned} \mathbf{B} &= \frac{\mu_0 I}{2 \pi r} \\ \mathbf{B} &= \frac{4\pi \times 10^{-7} \times 5}{2\pi \times 0.1} \\ \mathbf{B} &= \frac{2 \times 10^{-6}}{0.1} \\ \mathbf{B} &= 2 \times 10^{-5} \, \text{T} \end{aligned}$

Applications of Vector Fields

1. Electromagnetism

Vector fields describe electric and magnetic fields, which are fundamental in understanding electromagnetic force and waves.

2. Fluid Dynamics

Velocity fields in fluid dynamics help in analyzing fluid flow, turbulence, and aerodynamics.

3. Meteorology

Wind velocity fields are used in weather prediction and climate studies.

4. Gravitational Fields

In gravitational studies, vector fields depict the gravitational forces exerted by massive objects. They are used to analyze planetary motion, understand the behavior of objects in gravitational fields, and study the dynamics of galaxies and other celestial bodies.

5. Robotics and Navigation

Vector fields assist in path planning and navigation for robots and autonomous vehicles. They help in determining optimal routes, avoiding obstacles, and ensuring efficient movement in various environments.