Work and Mechanical Energy
Understanding the concepts of work and mechanical energy is crucial for mastering the principles of energy transfer and conservation in the AP Physics exam. Below are detailed notes to help you achieve a high score on your AP Physics exam.
Learning Objectives
By studying Work and Mechanical Energy, you will understand the relationship between force, displacement, and energy transfer. You will learn to calculate work done by various forces, comprehend kinetic and potential energy, and apply the Work-Energy Theorem. You’ll explore energy conservation principles in closed systems, analyze power, and solve problems involving mechanical advantage and efficiency in machines. Mastery of these concepts will enable you to solve complex physics problems and excel in the AP Physics exam.
Definition of Work
Work: Work is done when a force applied to an object causes a displacement. It is a scalar quantity, meaning it has magnitude but no direction.
Formula: W = F⋅d = Fdcosθ
where:
- W is work,
- F is the applied force,
- d is the displacement,
- θ is the angle between the force and displacement vectors.
Units: The units of work are joules (J), where 1 joule = 1 newton meter (N·m).
Characteristics
- Scalar Quantity: Work has magnitude but no direction.
- Units: The SI unit of work is the joule (J).
- Positive and Negative Work: Work is positive if the force and displacement are in the same direction, and negative if they are in opposite directions.
Positive, Negative, and Zero Work
- Positive Work: When the force and displacement are in the same direction \[ 0^\circ \leq \theta < 90^\circ \].
- Negative Work: When the force and displacement are in opposite directions \[ 90^\circ < \theta \leq 180^\circ \].
- Zero Work: When the force is perpendicular to the displacement (θ=90ᵒ) or when there is no displacement.
Mechanical Energy
Mechanical Energy: Mechanical energy is the sum of kinetic energy and potential energy in a system. It is the energy associated with the motion and position of an object.
Kinetic Energy
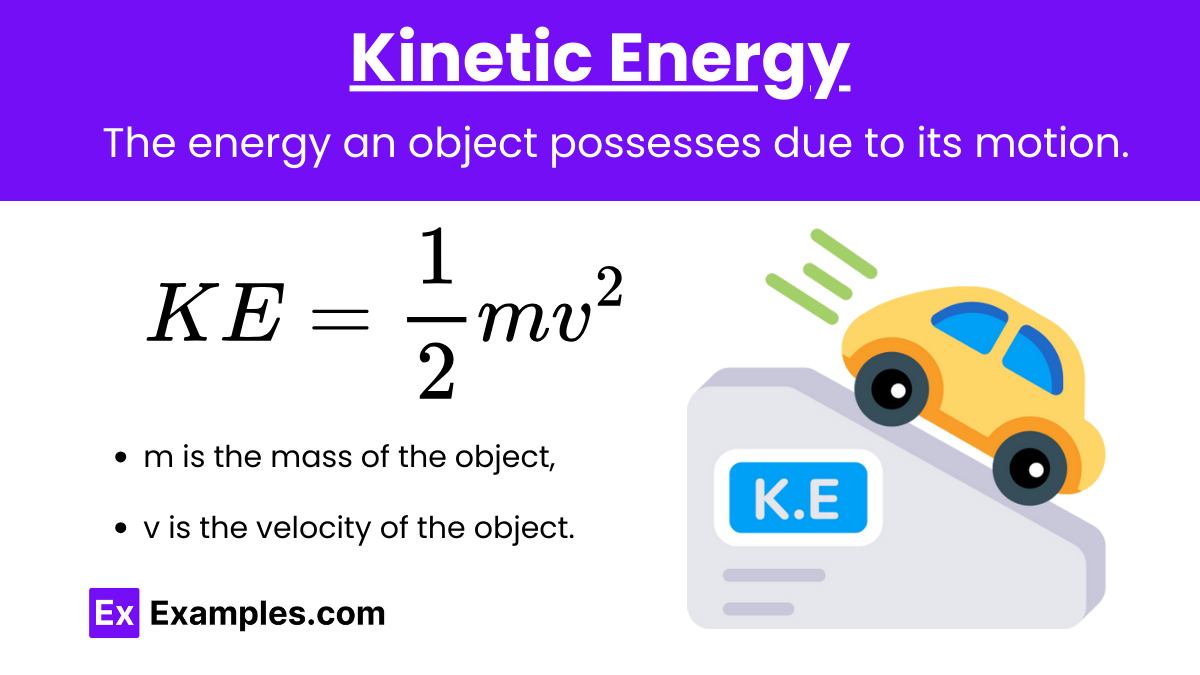
Kinetic Energy (KE): The energy an object possesses due to its motion.
Formula: \[ KE = \frac{1}{2} mv^2 \]
where:
- m is the mass of the object,
- v is the velocity of the object.
Potential Energy
Potential Energy (PE): The energy an object possesses due to its position or configuration.
Gravitational Potential Energy: PE =mgh
where:
- m is the mass,
- g is the acceleration due to gravity,
- h is the height above a reference point.
Elastic Potential Energy: \[ PE_{\text{elastic}} = \frac{1}{2} k x^2 \]
where:
- k is the spring constant,
- x is the displacement from the equilibrium position.
Conservation of Mechanical Energy
Conservation of Mechanical Energy: In the absence of non-conservative forces (like friction), the total mechanical energy of a system remains constant.
Formula: KEᵢ+PEᵢ = KEբ+PEբ
where:
- KEᵢ and PEᵢ are the initial kinetic and potential energies,
- KEբ and PEբ are the final kinetic and potential energies.
Work-Energy Theorem
Work-Energy Theorem: The work done on an object is equal to the change in its kinetic energy.
Formula: W = ΔKE = KEբ − KEᵢ
Examples and Problems
Example 1: Calculating Work
Scenario: A 10 N force is applied to push a box 5 meters across a floor. The force is applied at an angle of 30° to the horizontal.
Solution: \[ \begin{aligned} W &= Fd \cos \theta \\ W &= 10 \times 5 \times \cos 30^\circ \\ W &= 50 \times \frac{\sqrt{3}}{2} \\ W &= 25\sqrt{3} \, \text{J} \approx 43.3 \, \text{J} \end{aligned} \]
Example 2: Kinetic Energy
Scenario: A car of mass 1000 kg is moving with a velocity of 20 m/s. Calculate its kinetic energy.
Solution: \[ \begin{aligned} KE &= \frac{1}{2}mv^2 \\ KE &= \frac{1}{2} \times 1000 \times 20^2 \\ KE &= 500 \times 400 \\ KE &= 200,000 \, \text{J} \end{aligned} \]
Example 3: Gravitational Potential Energy
Scenario: A 2 kg object is lifted to a height of 10 meters. Calculate its gravitational potential energy.
Solution: \[ \begin{aligned} PE &= mgh \\ PE &= 2 \times 9.8 \times 10 \\ PE &= 196 \, \text{J} \end{aligned} \]
Example 4: Conservation of Mechanical Energy
Scenario: A roller coaster car of mass 500 kg is at the top of a 20 m hill and is moving at 5 m/s. Calculate its total mechanical energy at the top and at the bottom of the hill (neglecting friction).
At the Top: \[ \begin{aligned} KE_{\text{top}} &= \frac{1}{2}mv^2 = \frac{1}{2} \times 500 \times 5^2 = 6250 \, \text{J} \\ PE_{\text{top}} &= mgh = 500 \times 9.8 \times 20 = 98,000 \, \text{J} \\ E_{\text{total, top}} &= KE_{\text{top}} + PE_{\text{top}} = 6250 + 98,000 = 104,250 \, \text{J} \end{aligned} \]
At the Bottom: \[ \begin{aligned} PE_{\text{bottom}} &= 0 \, \text{J} \\ KE_{\text{bottom}} &= E_{\text{total, top}} = 104,250 \, \text{J} \end{aligned} \]
Applications
1. Roller Coasters
- Work: The work done by the motor to lift the coaster to the top of the first hill converts to gravitational potential energy.
- Mechanical Energy: As the coaster descends, potential energy converts to kinetic energy, making it move faster.
2. Pendulums
- Work: Work is done on a pendulum to lift it to a height.
- Mechanical Energy: The potential energy at the highest point converts to kinetic energy as it swings down and back to potential energy as it rises.
3. Projectile Motion
- Work: Work is done to launch a projectile.
- Mechanical Energy: The initial kinetic energy and potential energy at the launch point convert back and forth during the projectile’s flight.
4. Springs and Elastic Materials
- Work: Work is done to compress or stretch a spring.
- Mechanical Energy: The work is stored as elastic potential energy, which can convert to kinetic energy when the spring is released.
5. Hydroelectric Power Plants
- Work: Water at a height has gravitational potential energy.
- Mechanical Energy: As water flows down, potential energy converts to kinetic energy, which turns turbines to generate electricity.