Understanding Magnetic Fields and Forces is crucial in physics as they describe interactions between moving charges and magnetic materials. This topic covers the creation and behavior of magnetic fields, the forces they exert on charges and current-carrying wires, and the principles behind electromagnetic induction. Mastery of these concepts, including the right-hand rule, Lorentz force, and the applications of magnetic forces in technology, is essential for success in the AP Physics exam.
Free AP Physics 2: Algebra-Based Practice Test
Learning Objectives
Learn to define and represent magnetic fields, understand the sources and strengths of these fields, and apply the right-hand rule to determine their directions. Grasp the concepts of magnetic force on a moving charge and a current-carrying wire, understand the Lorentz force, and explore the interactions between parallel currents. Additionally, study electromagnetic induction, magnetic materials, and practical applications like motors and generators.
Magnetic Fields
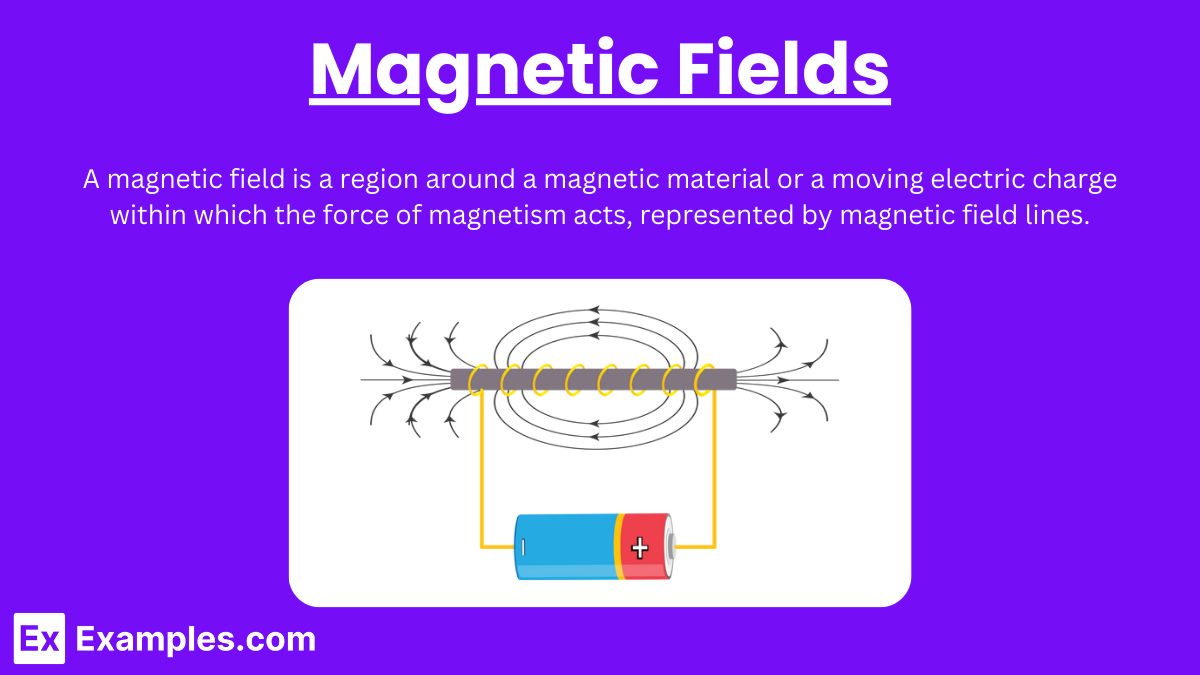
A magnetic field is a region around a magnetic material or a moving electric charge within which the force of magnetism acts.
Representation
Magnetic fields are represented by magnetic field lines. These lines:
Emerge from the north pole of a magnet.
Enter the south pole.
Never intersect.
Magnetic Field Strength
The strength of a magnetic field is measured in teslas (T).
A smaller unit is the gauss (G), where 1 T = 10,000 G.
Sources of Magnetic Fields
Permanent Magnets: Objects that produce their own persistent magnetic field.
Current-Carrying Wires: Moving electric charges create a magnetic field around the wire.
Magnetic Field of a Straight Current-Carrying Wire
The magnetic field (B) around a long, straight current-carrying wire is given by:
B = \frac{\mu_0 I}{2 \pi r}
μ₀ is the permeability of free space (4π×10⁻⁷ T m/A),
I is the current,
r is the distance from the wire.
Right-Hand Rule
The direction of the magnetic field around a current-carrying wire can be determined using the right-hand rule
Point your thumb in the direction of the current.
Your curled fingers show the direction of the magnetic field lines.
Magnetic Forces
Force on a Moving Charge
A charge (q) moving with velocity (v) in a magnetic field (B) experiences a force (F) given by: F=qv×B
This force is perpendicular to both the velocity of the charge and the magnetic field.
The magnitude of the force is: F=qvBsin(θ)where θ is the angle between v and B.
Lorentz Force
The total force on a charged particle moving in both electric (E) and magnetic fields is called the Lorentz force: F=q(E+v×B)
Force on a Current-Carrying Wire
A current-carrying wire in a magnetic field experiences a force given by:
F=IL×B
where:
I is the current,
L is the length vector of the wire in the direction of the current,
B is the magnetic field.
Magnetic Force Between Two Parallel Wires
Two parallel current-carrying wires exert a force on each other. The force per unit length (F/L) between two wires separated by a distance (d) is:
\frac{F}{L} = \frac{\mu_0 I_1 I_2}{2 \pi d}
If currents flow in the same direction, the wires attract.
If currents flow in opposite directions, the wires repel.
Applications of Magnetic Fields and Forces
Electromagnetic Induction
Faraday's Law of Induction states that a changing magnetic field within a closed loop induces an electromotive force (emf) in the wire:
\mathcal{E} = -\frac{d\Phi_B}{dt}
Magnetic Materials
Diamagnetic: Weakly repel magnetic fields.
Paramagnetic: Weakly attract magnetic fields.
Ferromagnetic: Strongly attract magnetic fields and can be permanently magnetized.
Examples Of Magnetic Fields and Forces
1. Earth’s Magnetic Field
The Earth itself acts as a giant magnet with a magnetic field that extends from the core into space. This field protects the planet from solar wind and cosmic radiation and causes the phenomenon of the auroras at the poles.
2. Electromagnets
Electromagnets are created by running an electric current through a coil of wire wrapped around a magnetic core. They are used in various devices, including electric bells, magnetic locks, and relays.
3. Magnetic Force on a Current-Carrying Wire
When a wire carrying an electric current is placed in a magnetic field, it experiences a force perpendicular to both the current and the field. This principle is used in electric motors to convert electrical energy into mechanical motion.
4. Induction Cooktops
Induction cooktops use electromagnetic induction to heat cookware. An alternating current in a coil beneath the cooktop generates a magnetic field, which induces electric currents in the ferromagnetic cookware, producing heat.
5. Magnetic Resonance Imaging (MRI)
MRI machines use strong magnetic fields and radio waves to generate detailed images of the body’s internal structures. The magnetic fields align the nuclei of hydrogen atoms in the body, and radio waves perturb this alignment, producing signals that are converted into images.
Practice Test Questions on Magnetic Fields and Forces
Question 1
Which of the following correctly describes the direction of the magnetic force on a positive charge moving in a magnetic field?
a) In the direction of the magnetic field
b) Opposite to the magnetic field
c) Perpendicular to both the velocity of the charge and the magnetic field
d) In the direction of the charge's velocity
Answer: c) Perpendicular to both the velocity of the charge and the magnetic field
Explanation: The magnetic force on a moving charge is given by the Lorentz force law, F=qv×B. This cross product means that the force is perpendicular to both the velocity (v) of the charge and the magnetic field (B). The right-hand rule helps determine this direction.
Question 2
What happens to the magnetic field strength inside a solenoid if the current is doubled while keeping all other factors constant?
a) It remains unchanged.
b) It doubles.
c) It halves.
d) It quadruples.
Answer: b) It doubles.
Explanation: The magnetic field strength (B) inside a solenoid is directly proportional to the current (I) passing through it. The relationship is given by B = \mu_0 \frac{N}{L} I , where μ0 is the permeability of free space, N is the number of turns, and L is the length of the solenoid. Doubling the current doubles the magnetic field strength.
Question 3
Two parallel wires carry currents in the same direction. What type of force do they exert on each other?
a) They repel each other.
b) They attract each other.
c) There is no force between them.
d) They spin around each other.
Answer: b) They attract each other.
Explanation: According to Ampère's law, two parallel current-carrying wires exert forces on each other. If the currents flow in the same direction, the magnetic fields produced by each wire interact in such a way that they attract each other. This is due to the right-hand rule and the nature of magnetic field lines around the wires.