Angular Momentum and its Conservation
Angular momentum is a crucial concept in rotational dynamics, representing the quantity of motion an object has while rotating around an axis. In AP Physics, understanding angular momentum and its conservation is essential for analyzing systems where rotational motion occurs, such as spinning objects or planetary orbits. The principle of conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant, making it a powerful tool in solving complex rotational problems.
Learning Objectives
By studying Angular Momentum and its Conservation for the AP Physics exam, you should aim to understand the definition and mathematical formulation of angular momentum, including its relationship with moment of inertia and angular velocity. You should be able to apply the principle of conservation of angular momentum in isolated systems, analyze situations involving external torques, and solve problems that require calculating angular momentum in both point particles and rigid bodies. Mastery of these concepts will enable you to predict and explain rotational motion in various physical scenarios.
What is Angular Momentum?
Angular momentum (L) is a vector quantity that represents the product of a rotating object’s moment of inertia and its angular velocity. It can be thought of as a measure of how much rotational motion an object has.
Mathematically, angular momentum is defined as:
\( \mathbf{L} = \mathbf{r} \times \mathbf{p} \)
Where:
- L is the angular momentum.
- r is the position vector (distance from the point of rotation).
- p is the linear momentum ( p=mv, where m is mass and v is velocity).
- × denotes the cross product, indicating that angular momentum is perpendicular to the plane formed by r and p.
In terms of moment of inertia (I) and angular velocity (ω): \( \mathbf{L} = I \omega \)
Where:
- I is the moment of inertia, which depends on the mass distribution relative to the axis of rotation.
- ω is the angular velocity vector.
Moment of Inertia
The moment of inertia is a scalar quantity that measures an object’s resistance to changes in its rotational motion. It depends on both the mass of the object and how that mass is distributed relative to the axis of rotation.
For common shapes:
- Solid Sphere: \( I = \frac{2}{5} M R^2 \)
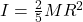
- Solid Cylinder (about central axis): \( I = \frac{1}{2} M R^2 \)
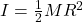
- Thin Rod (about end): \( I = \frac{1}{3} M L^2 \)
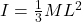
Where M is the mass, R is the radius, and L is the length of the object.
Conservation of Angular Momentum
Angular momentum is conserved in a closed system with no external torques. This principle is analogous to the conservation of linear momentum and is expressed as:
\( \mathbf{L}_{\text{initial}} = \mathbf{L}_{\text{final}} \)
Or, in a system where moment of inertia can change:
\( I_{\text{initial}} \omega_{\text{initial}} = I_{\text{final}} \omega_{\text{final}} \)
If no external torque acts on a system, the total angular momentum of the system remains constant.
Torque and Angular Momentum
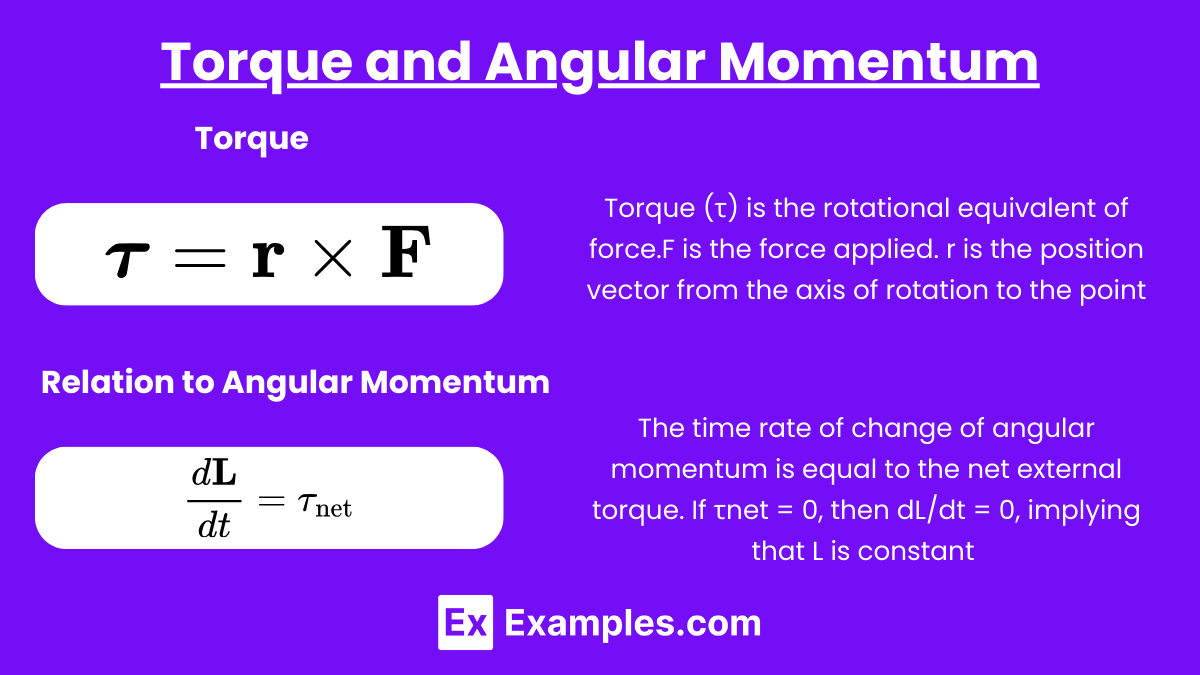
Torque (τ) is the rotational equivalent of force. It causes a change in angular momentum and is defined as:
\( \boldsymbol{\tau} = \mathbf{r} \times \mathbf{F} \)
Where:
- F is the force applied.
- r is the position vector from the axis of rotation to the point where the force is applied.
Relation to Angular Momentum:
The time rate of change of angular momentum is equal to the net external torque acting on the system:
\( \frac{d\mathbf{L}}{dt} = \tau_{\text{net}} \)
If τnet = 0, then dL/dt = 0, implying that L is constant (i.e., angular momentum is conserved).
Applications of Angular Momentum Conservation
- Gyroscopes: Gyroscopes maintain their orientation due to the conservation of angular momentum, which makes them useful in navigation systems.
- Astrophysics: Conservation of angular momentum explains phenomena like the flattening of rotating galaxies and the formation of accretion disks around black holes.
- Everyday Examples: Ice skaters, divers, and even rotating playground equipment all provide observable demonstrations of angular momentum and its conservation.
- Rocket Propulsion: During space maneuvers, rockets conserve angular momentum by firing thrusters that create a torque, allowing them to change orientation without external forces. This principle is crucial for spacecraft navigation and attitude control.
- Planetary Formation: In the early solar system, the conservation of angular momentum played a key role in the formation of planets. As gas and dust clouds collapsed under gravity, they spun faster, leading to the formation of rotating protoplanetary disks from which planets eventually formed.
Examples
Example 1: Figure Skater Spinning
When a figure skater pulls their arms in during a spin, they spin faster. This happens because when the skater reduces their moment of inertia by bringing their arms closer to their body, their angular velocity increases to conserve angular momentum. The product of moment of inertia and angular velocity remains constant, demonstrating the conservation of angular momentum.
Example 2: Bicycle Wheel Gyroscope
A spinning bicycle wheel can be used as a gyroscope. When you tilt the axis of the spinning wheel, the direction of the wheel’s axis changes in a way that conserves angular momentum. The wheel resists changes in its orientation due to the conservation of angular momentum, which explains why gyroscopes are used for stabilization in various technologies.
Example 3: Earth’s Orbit Around the Sun
The Earth’s orbit is an example of angular momentum conservation on a cosmic scale. As Earth moves around the Sun, its distance from the Sun changes slightly over the course of the year. When Earth is closer to the Sun (at perihelion), it moves faster; when it is farther away (at aphelion), it moves slower. This variation in speed ensures that the Earth’s angular momentum remains conserved throughout its orbit.
Example 4: Divers Changing Position Mid-Air
Divers often change their body position during a dive to control their rotation speed. By tucking in their limbs, divers decrease their moment of inertia, which increases their rotation speed to conserve angular momentum. When they spread out their arms and legs before entering the water, their rotation slows down, showcasing angular momentum conservation in real time.
Example 5: Neutron Stars
Neutron stars, which are remnants of supernovae, exhibit angular momentum conservation on an astronomical scale. As a star collapses into a neutron star, its radius dramatically decreases, leading to an enormous increase in its rotation speed to conserve angular momentum. This is why neutron stars, despite their small size, can spin incredibly fast, sometimes hundreds of times per second.
Multiple Choice Questions
Question 1
A figure skater is spinning with her arms extended. When she pulls her arms in close to her body, what happens to her angular velocity and why?
A) Her angular velocity decreases because her moment of inertia increases.
B) Her angular velocity increases because her moment of inertia decreases.
C) Her angular velocity stays the same because angular momentum is conserved.
D) Her angular velocity decreases because angular momentum is not conserved.
Answer: B
Explanation: When the skater pulls her arms in, her moment of inertia decreases. According to the conservation of angular momentum, if no external torque acts on the system, the angular momentum (L) remains constant. Angular momentum is given by L = Iω, where I is the moment of inertia and ω is the angular velocity. Since L is constant and I decreases, ω must increase to compensate. Thus, the skater spins faster when her arms are pulled in.
Question 2
A solid disk and a ring of the same mass and radius are both spinning at the same angular velocity. Which object has greater angular momentum?
A) The solid disk because it has a greater mass.
B) The ring because it has a greater moment of inertia.
C) Both have the same angular momentum because they have the same angular velocity.
D) The solid disk because it has a smaller radius.
Answer: B
Explanation: The angular momentum L of an object is given by L = Iω, where I is the moment of inertia and ω\omegaω is the angular velocity. For a solid disk, the moment of inertia is Idisk = 1/2MR2, and for a ring, it is Iring=MR2. Since the ring has a greater moment of inertia (twice that of the solid disk for the same mass and radius), and both have the same angular velocity ω, the ring has greater angular momentum.
Question 3
A planet orbits a star in an elliptical path. At which point in its orbit does the planet have the greatest angular momentum?
A) At the point closest to the star (perihelion).
B) At the point farthest from the star (aphelion).
C) The angular momentum is the same at all points in the orbit.
D) At a point midway between perihelion and aphelion.
Answer: C
Explanation: Angular momentum is conserved in the absence of external torques. For a planet orbiting a star, the gravitational force acts along the radius, providing no torque about the star, so the angular momentum of the planet is conserved throughout its orbit. This means the angular momentum remains the same at all points in the orbit, whether the planet is at perihelion, aphelion, or any other point. Hence, the correct answer is that the angular momentum is the same at all points in the orbit.