Center of Mass
The center of mass is a fundamental concept in AP Physics that represents the point where the mass of an object or system is evenly distributed. It serves as the balance point, crucial for understanding both translational and rotational motion. In AP Physics, mastering the concept of center of mass is essential for analyzing complex systems, predicting motion, and solving problems related to collisions, stability, and rotational dynamics, making it a vital topic for achieving success in the exam.
Learning Objectives
When studying Center of Mass for the AP Physics exam, you should focus on understanding how to calculate the center of mass for both discrete and continuous systems, and interpret its significance in physical situations. Grasp the relationship between center of mass and translational motion, including how it applies to momentum and collisions. Learn to apply these principles in two and three dimensions, and connect them to rotational dynamics and real-world applications, such as orbital mechanics. Practice problem-solving to reinforce these concepts.
What is Center of Mass?
The center of mass (COM) is a critical concept in physics that represents the average location of all the mass in a system. It is the point where you can consider the entire mass of an object or system to be concentrated for purposes of analysis of translational motion. For symmetrical objects with uniform density, the center of mass coincides with the geometric center. However, for irregularly shaped objects or non-uniform density distributions, the center of mass is not always located at the geometric center.
For a system of particles, the center of mass is given by:
\( \vec{R}_{cm} = \frac{1}{M} \sum_{i} \left( m_i \vec{r}_i \right) \)
Where:
- Rcm is the position vector of the center of mass.
- M is the total mass of the system (M = ∑mi).
- mi is the mass of the ith particle.
- ri is the position vector of the ith particle.
Importance of Center of Mass
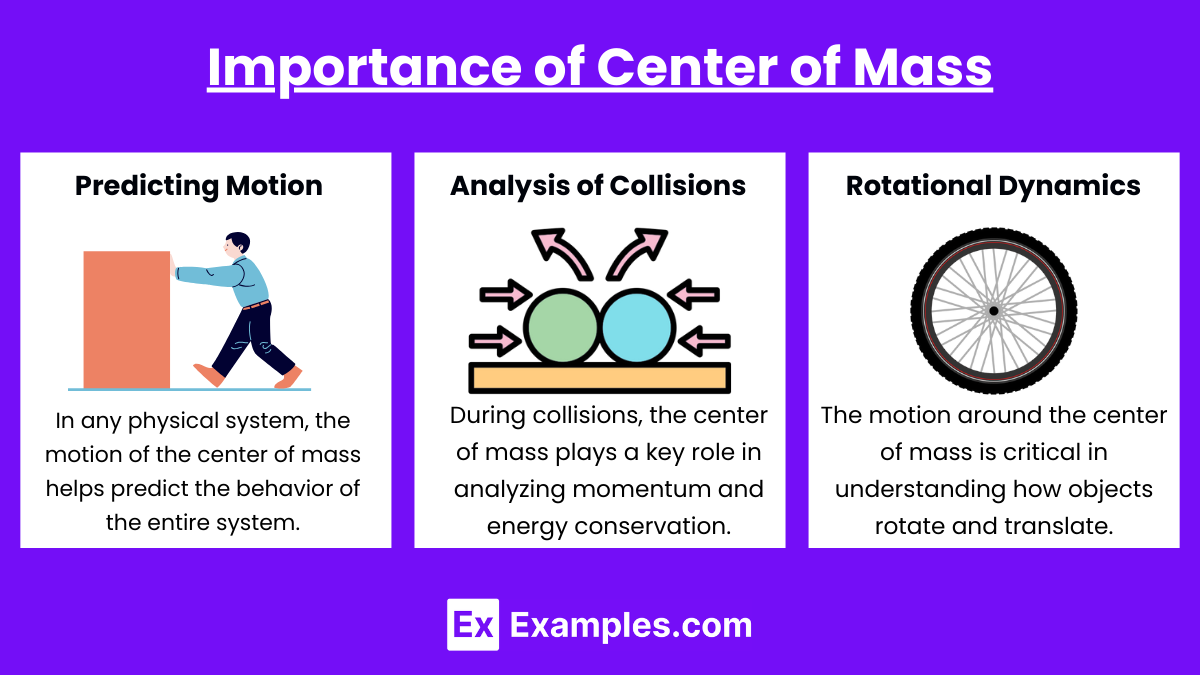
Understanding the center of mass is essential in various physics applications:
- Predicting Motion: In any physical system, the motion of the center of mass helps predict the behavior of the entire system.
- Analysis of Collisions: During collisions, the center of mass plays a key role in analyzing momentum and energy conservation.
- Rotational Dynamics: The motion around the center of mass is critical in understanding how objects rotate and translate.
Calculating Center of Mass
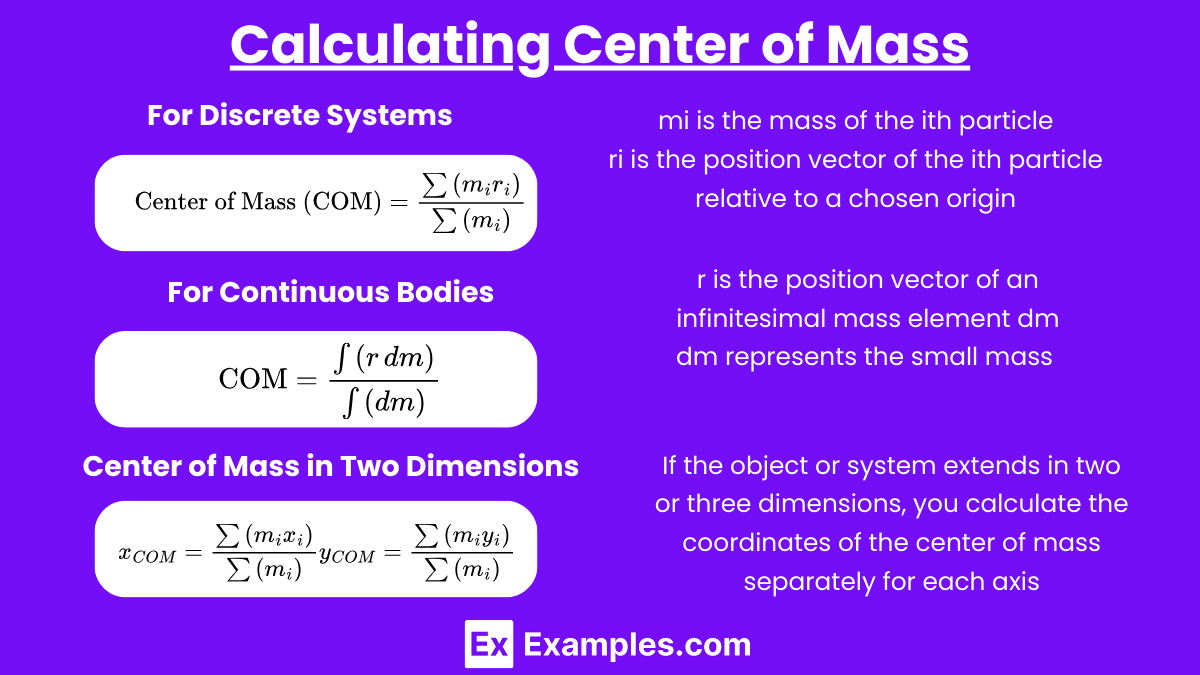
For Discrete Systems
For a system of particles, the center of mass can be calculated using the following formula:
\( \text{Center of Mass (COM)} = \frac{\sum \left( m_i r_i \right)}{\sum \left( m_i \right)} \)
Where:
- mi is the mass of the ith particle
- ri is the position vector of the ith particle relative to a chosen origin
For Continuous Bodies
For a continuous mass distribution, the center of mass is calculated using an integral:
\(\text{COM} = \frac{\int \left( r \, dm \right)}{\int \left( dm \right)} \)
Where:
- r is the position vector of an infinitesimal mass element dm
- dm represents the small mass element of the object
Center of Mass in Two or Three Dimensions
If the object or system extends in two or three dimensions, you calculate the coordinates of the center of mass separately for each axis:
- In Two Dimensions:
- \( x_{COM} = \frac{\sum \left( m_i x_i \right)}{\sum \left( m_i \right)} \)
- \( y_{COM} = \frac{\sum \left( m_i y_i \right)}{\sum \left( m_i \right)} \)
- In Three Dimensions:
- \( x_{COM} = \frac{\sum \left( m_i x_i \right)}{\sum \left( m_i \right)} \)
- \( y_{COM} = \frac{\sum \left( m_i y_i \right)}{\sum \left( m_i \right)} \)
- \( z_{COM} = \frac{\sum \left( m_i z_i \right)}{\sum \left( m_i \right)} \)
Applications of Center of Mass
1. Motion of Center of Mass
- The velocity (vCOM) and acceleration (aCOM) of the center of mass can be calculated similarly to the position: \( \vec{v}_{COM} = \frac{\sum \left( m_i \vec{v}_i \right)}{\sum \left( m_i \right)}, \quad \vec{a}_{COM} = \frac{\sum \left( m_i \vec{a}_i \right)}{\sum \left( m_i \right)} \)
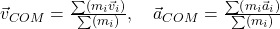
- This is particularly useful in analyzing the motion of systems where different parts might move differently, such as in explosions or collisions.
2. Center of Mass and Rotational Motion
- When analyzing rotational motion, the axis of rotation often passes through the center of mass.
- Torque (τ) acting on a body about its center of mass is related to angular acceleration (α) by: 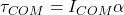\( \tau_{COM} = I_{COM} \alpha \) where ICOM is the moment of inertia about the center of mass.
3. Center of Mass in Space and Astrophysics
- In celestial mechanics, the center of mass (often called the barycenter) of two or more bodies in space determines their orbital motion. For example, Earth and the Moon orbit their common center of mass, which lies inside the Earth but not at its center.
Properties of Center of Mass
- Single Point Representation:
- The center of mass represents a point where the entire mass of a system or object can be considered to be concentrated for the purposes of analyzing translational motion.
- Depends on Mass Distribution:
- The position of the center of mass depends on the distribution of mass within the object or system. For symmetrical objects with uniform density, it typically lies at the geometric center.
- Motion of Center of Mass:
- The motion of the center of mass follows Newton’s laws, and it moves as if all external forces acting on the system were applied at that point. This holds true even if the system’s individual components are moving in different directions.
- Independent of Rotational Motion:
- The center of mass moves independently of the rotational motion of an object. This means that while an object can rotate around its center of mass, the translational motion of the center of mass itself is not affected by this rotation.
Examples
Example 1: Human Body
The center of mass in a human body typically lies near the belly button when standing upright. This point shifts depending on body position; for instance, if you bend forward, the center of mass moves forward too. Understanding this concept is crucial in sports and dance, where balance and stability depend on maintaining the center of mass over the base of support.
Example 2: Balancing a Ruler
When you balance a uniform ruler on your finger, the point where it remains steady is its center of mass. For a uniform object, this point is in the geometric center. The weight on either side of this point is equal, allowing it to balance perfectly.
Example 3: Solar System
The center of mass of the solar system is not at the center of the Sun but rather near or just outside its surface. This point, called the barycenter, is where the masses of the Sun and the planets balance out, and it’s the point around which they all orbit.
Example 4: Airplane in Flight
The center of mass in an airplane is a critical factor in its stability and control. It must be carefully calculated and maintained through proper loading of passengers, cargo, and fuel. If the center of mass is too far forward or backward, the plane could become difficult to control or even unsafe to fly.
Example 5: Double Star System
In a binary star system, two stars orbit around their common center of mass. This point lies closer to the more massive star, and both stars revolve around it. The position of this center of mass influences the orbital characteristics of the stars and is used by astronomers to study the mass and distance of such systems.
Multiple Choice Questions
Question 1
Where is the center of mass of a uniform, circular disk located?
- A) At the edge of the disk
- B) At the center of the disk
- C) Halfway between the center and the edge
- D) It depends on the thickness of the disk
Correct Answer: B) At the center of the disk
Explanation: For a uniform, circular disk, the mass is symmetrically distributed around its center. Therefore, the center of mass is located exactly at the geometric center of the disk.
Question 2
Which of the following objects has its center of mass outside the physical body of the object?
- A) A solid sphere
- B) A baseball bat
- C) A hollow ring
- D) A rectangular block
Correct Answer: C) A hollow ring
Explanation: For a hollow ring, the mass is distributed along the ring’s circumference, leaving the center of the ring empty. Hence, the center of mass is located at the geometric center of the ring, which is a point outside the physical material of the object.
Question 3
For a uniform ruler balanced at its center, what happens to the center of mass if you cut the ruler in half and only keep one piece?
- A) It stays in the same place
- B) It moves to the new center of the remaining piece
- C) It moves to one end of the remaining piece
- D) It becomes undefined
Correct Answer: B) It moves to the new center of the remaining piece
Explanation: When you cut the uniform ruler in half and keep one piece, the remaining piece is still uniform. The center of mass of a uniform object is at its geometric center, so the center of mass of the remaining half will be at its new midpoint.