Circular Motion

Last Updated: September 23, 2024

Notes

Circular motion is a fundamental concept in physics, describing the movement of an object along a circular path. This motion is governed by forces that act towards the center of the circle, causing the object to constantly change direction while maintaining a consistent speed. In AP Physics, understanding circular motion is crucial, as it underpins many advanced topics, including rotational dynamics and orbital motion. Mastery of this concept provides a solid foundation for tackling complex problems involving forces, energy, and acceleration.

Free AP Physics C: Mechanics Practice Test

Learning Objectives

When studying Circular Motion for the AP Physics exam, you should focus on understanding the key concepts of centripetal force and acceleration, how they relate to the motion of objects in circular paths, and the relationship between linear and angular quantities. You should also learn to apply Newton’s laws to circular motion scenarios, analyze non-uniform circular motion, and calculate relevant quantities like velocity, period, and frequency. Mastering these concepts will help you solve problems involving rotating systems, orbital motion, and practical applications of circular dynamics.

Basics of Circular Motion

Circular motion is a fundamental concept in physics that involves an object moving in a path along a circular trajectory. Understanding circular motion is crucial for scoring well on the AP Physics exam, as it ties into various other topics such as forces, energy, and dynamics.

Key Quantities

Radius (r): The distance from the center of the circle to the object in motion.
Period (T): The time it takes for one complete revolution around the circle.
Frequency (f): The number of revolutions per second. It is the inverse of the period f=1/T.
Angular Displacement (θ): The angle through which the object has moved, measured in radians.
Angular Velocity (ω): The rate of change of angular displacement, given by ω=Δθ/Δt. For uniform circular motion, ω=2π/T.

2. Centripetal Force and Centripetal Acceleration

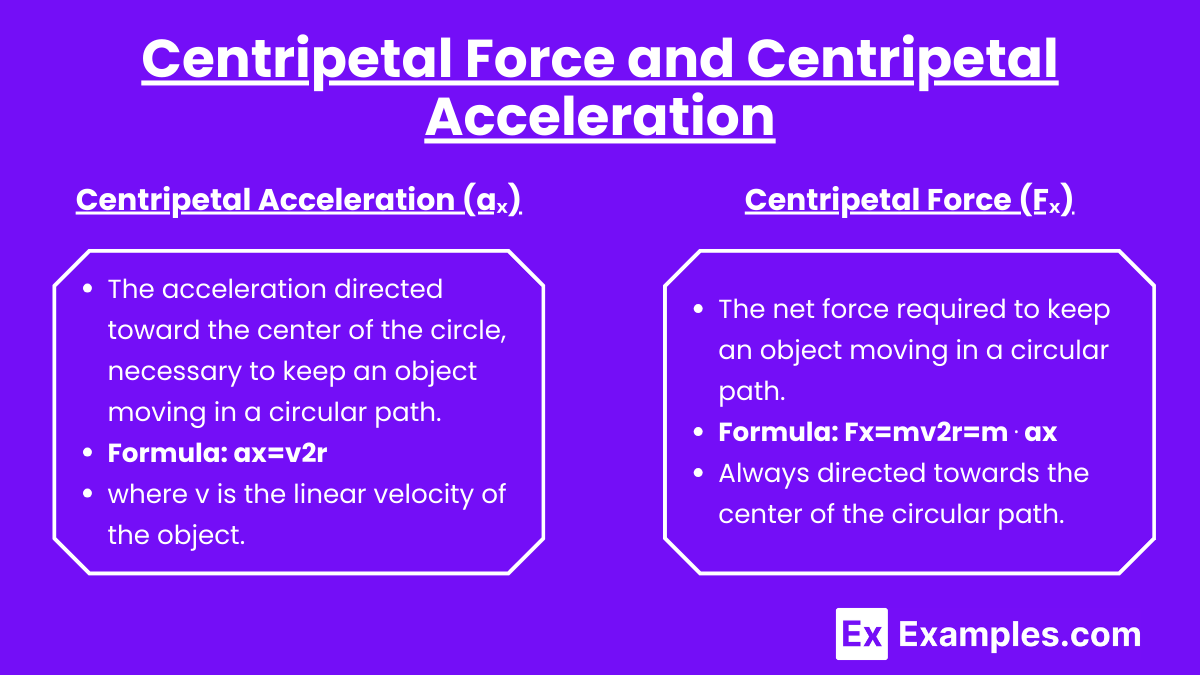
Centripetal Acceleration (aₓ)

The acceleration directed toward the center of the circle, necessary to keep an object moving in a circular path.
Formula: ax=v²r
where v is the linear velocity of the object.

Centripetal Force (Fₓ)

The net force required to keep an object moving in a circular path.
Formula: $F_{x} = \frac{mv^{2}}{r} = m \cdot a_{x}$ . where m is the mass of the object, v is its velocity, and rrr is the radius of the circle.
Direction: Always directed towards the center of the circular path.

Relationship Between Linear and Angular Quantities

Linear velocity (v): $v = \omega r$ $a_{x} = \omega^{2} r$
Centripetal Acceleration (in terms of angular velocity): $a_{x} = \omega^{2} r$

3. Dynamics of Circular Motion

Newton’s Second Law in Circular Motion

Application: In circular motion, Newton’s Second Law applies in the radial direction: $F_{x} = m a_{x}$
Sources of Centripetal Force: Depending on the context, centripetal force can arise from tension (in a string), gravitational force (in orbital motion), normal force (in a roller coaster loop), or friction (for a car rounding a curve).

4. Non-Uniform Circular Motion

Tangential Acceleration

The component of acceleration that is tangential to the circular path, responsible for changing the speed of the object in non-uniform circular motion.
Formula:
$a_{t} = \frac{d |v|}{dt}$
where ∣v∣ is the magnitude of the velocity.

Total Acceleration

In non-uniform circular motion, the total acceleration aaa is the vector sum of the centripetal acceleration a_x and the tangential acceleration

$a = \sqrt{a_{x}^{2} + a_{t}^{2}}$

5. Energy Considerations in Circular Motion

Kinetic Energy

Formula:
$K.E. = \frac{1}{2} mv^{2} = \frac{1}{2} m (\omega r)^{2}$
where v is the linear velocity, ω\omegaω is the angular velocity, and r is the radius.

Work and Power in Circular Motion

Work Done by a Centripetal Force: No work is done by the centripetal force since it is always perpendicular to the displacement of the object.
Power: In scenarios where there is tangential acceleration, power is given by:
$P = F_{t} \cdot v$
where F_t is the tangential force.

Examples

Example 1: Planetary Orbits

The motion of planets around the sun is a classic example of circular motion, or more precisely, elliptical motion where the orbits are nearly circular. The gravitational force between the sun and a planet acts as the centripetal force, pulling the planet toward the center of its orbit and keeping it in continuous circular motion.

Example 2: Ceiling Fan Blades

When a ceiling fan is turned on, its blades rotate in a circular path around the central hub. Each point on a fan blade follows a circular trajectory, driven by the motor’s force, which provides the necessary centripetal force to maintain this motion.

Example 3: Electrons in Magnetic Fields

In physics experiments or certain natural settings, electrons can move in circular paths when subjected to a perpendicular magnetic field. The magnetic force acts as the centripetal force, causing the electrons to spiral or move in circular orbits within the field.

Example 4: Merry-Go-Round

A merry-go-round in a playground exhibits circular motion as it spins around its central axis. The children sitting on the edge experience this motion, where the platform’s force provides the centripetal acceleration needed to keep them moving in a circular path.

Example 5: Car Turning in a Circular Track

When a car navigates a circular track, such as in a roundabout, it undergoes circular motion. The friction between the tires and the road provides the centripetal force necessary to keep the car moving along the curved path without sliding outward due to inertia.

Multiple Choice Questions

Question 1

A car is moving at a constant speed around a circular track. Which of the following statements is true about the car’s acceleration?

A) The car has zero acceleration because its speed is constant.
B) The car has a constant acceleration directed towards the center of the circle.
C) The car has a varying acceleration directed tangentially to the circle.
D) The car has a constant acceleration directed away from the center of the circle.

Correct Answer: B) The car has a constant acceleration directed towards the center of the circle.

Explanation:
Even though the car’s speed is constant, it is undergoing centripetal acceleration because the direction of its velocity is continuously changing as it moves around the circular track. This acceleration always points towards the center of the circle, perpendicular to the car’s velocity. This is why option B is correct. Option A is incorrect because acceleration is not zero; option C is wrong because the acceleration is not varying and is not directed tangentially; and option D is incorrect because acceleration in circular motion is always directed toward the center, not away from it.

Question 2

If the radius of a circular path is doubled while keeping the speed of an object constant, what happens to the centripetal force required to maintain the object in circular motion?

A) The centripetal force is halved.
B) The centripetal force is doubled.
C) The centripetal force remains the same.
D) The centripetal force is reduced to one-fourth.

Correct Answer: A) The centripetal force is halved.

Explanation:
The centripetal force F_c required for circular motion is given by the formula:

$F_{c} = \frac{mv^{2}}{r}$

where m is the mass of the object, v is its speed, and r is the radius of the circular path. If the radius r is doubled, the force Fc becomes:

$F'_{c} = \frac{mv^{2}}{2r} = \frac{1}{2} \times \frac{mv^{2}}{r}$

This shows that the centripetal force is halved when the radius is doubled, making option A correct. Option B is incorrect because doubling the radius does not increase the force; option C is wrong because the force does change; and option D is incorrect as the force is not reduced to one-fourth.

Question 3:
A satellite is orbiting the Earth in a circular orbit at a constant speed. What happens to the satellite’s velocity if the gravitational force between the satellite and Earth suddenly disappears?

A) The satellite will continue moving in a circular orbit with the same speed.
B) The satellite will move in a straight line at a constant speed.
C) The satellite will spiral into Earth.
D) The satellite will stop moving instantly.

Correct Answer: B) The satellite will move in a straight line at a constant speed.

Explanation:
If the gravitational force between the satellite and Earth suddenly disappears, the centripetal force that keeps the satellite in circular motion also vanishes. According to Newton’s First Law of Motion (inertia), an object in motion will continue in a straight line at constant speed unless acted upon by an external force. Therefore, the satellite will no longer follow a curved path but will instead continue in a straight line tangent to the point where the force disappeared, making option B correct. Option A is incorrect because the circular motion cannot continue without centripetal force; option C is wrong because the satellite will not spiral into Earth without gravitational force; and option D is incorrect because the satellite cannot stop instantly without an external force acting on it.