Forces and potential energy are fundamental concepts in AP Physics that describe how objects interact and how energy is stored in systems. Forces cause objects to accelerate, change direction, or alter their state of motion, and they come in various forms like gravitational, normal, and frictional forces. Potential energy, on the other hand, is the energy stored in an object due to its position or configuration, such as an object’s height above the ground or a compressed spring. Understanding these principles is crucial for mastering mechanics in AP Physics.
Learning Objectives
In studying Forces and Potential Energy for the AP Physics exam, you should aim to understand the different types of forces, such as gravitational, normal, and frictional forces, and how they interact with objects. Learn to apply Newton’s Laws of Motion to analyze the effects of these forces on motion. Grasp the concepts of potential energy, particularly gravitational and elastic potential energy, and understand how energy conservation principles relate to mechanical systems. Master problem-solving techniques involving free-body diagrams, energy conservation, and force analysis.
Introduction to Forces

Force is a vector quantity that causes an object to accelerate, change direction, or alter its shape. The unit of force is the Newton (N). The direction of the force vector is crucial, as it determines how the object will move or change its state.
Types of Forces
- Gravitational Force (Fgravity):
- The force of attraction between two masses.
- Acts downward towards the center of the Earth.
- Formula: Fg=mg , where m is mass and g is the acceleration due to gravity (9.8 m/s2).
- Normal Force (Fnormal):
- The perpendicular force exerted by a surface on an object in contact with it.
- Balances the gravitational force in cases where the object is resting on a horizontal surface.
- Frictional Force (Ffriction):
- The force that opposes the motion of an object.
- Types: Static friction (prevents motion) and Kinetic friction (opposes ongoing motion).
- Formula: Ff=μFn, where μ is the coefficient of friction and Fn is the normal force.
- Tension Force (Ftension):
- The force transmitted through a string, rope, or cable when it is pulled tight by forces acting from opposite ends.
- Acts along the length of the wire and is uniform throughout.
- Spring Force (Fspring):
- The force exerted by a compressed or stretched spring.
- Hooke’s Law: Fs=−kx, where k is the spring constant and x is the displacement from the equilibrium position.
- Applied Force (Fapplied):
- Any force that is applied to an object by a person or another object.
Newton’s Laws of Motion

Newton’s Laws of Motion are three fundamental principles that describe the relationship between the motion of an object and the forces acting on it.
- First Law (Law of Inertia):
- An object will remain at rest or in uniform motion unless acted upon by a net external force.
- Second Law (Law of Acceleration):
- The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
- Formula: F = ma.
- Third Law (Action and Reaction):
- For every action, there is an equal and opposite reaction.
Potential Energy

Potential Energy (U) is the stored energy of an object due to its position or configuration. It can be transformed into kinetic energy when the object is set in motion.
The formula for Potential Energy (PE) is:
PE = mgh
Where:
- PE is the potential energy,
- m is the mass of the object,
- g is the acceleration due to gravity (usually 9.8 m/s2 on Earth),
- h is the height of the object above a reference point.
Types of Potential Energy

- Gravitational Potential Energy (Ugravity):
- Energy stored due to an object’s height above the ground.
- Formula: Ug = mgh, where h is the height above the reference point.
- Elastic Potential Energy (Uspring):
- Energy stored in a spring when it is compressed or stretched.
- Formula: Us = 1/2kx2.
- where k is the spring constant (a measure of the stiffness of the spring), and x is the displacement from the spring’s equilibrium position.
Relationship Between Forces and Potential Energy
- Work-Energy Principle:
- The work done by all forces acting on an object equals the change in the object’s kinetic energy.
- W=ΔK=F⋅d, where d is the displacement.
- Conservative Forces:
- Forces for which the work done does not depend on the path taken but only on the initial and final positions.
- Examples: Gravitational force, spring force.
- For conservative forces, potential energy can be defined.
- Non-Conservative Forces:
- Forces that cause energy to be lost from the system, typically as thermal energy.
- Examples: Friction, air resistance.
- Conservation of Mechanical Energy:
- In the absence of non-conservative forces, the total mechanical energy (kinetic + potential) remains constant.Etotal=K+U=constant.
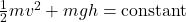
- In the absence of non-conservative forces, the total mechanical energy (kinetic + potential) remains constant.Etotal=K+U=constant.
Problem-Solving Strategies
- Free-Body Diagrams:
- Draw all forces acting on the object.
- Identify the direction and magnitude of each force.
- Identify Conservative and Non-Conservative Forces:
- Determine if energy is conserved or if energy loss needs to be accounted for.
- Apply Newton’s Laws:
- Use F=ma to relate forces to acceleration and motion.
- Use Energy Methods:
- For problems involving heights and springs, consider using energy conservation principles instead of kinematic equations.
Examples
Example 1: Gravitational Potential Energy of a Book on a Shelf
When you lift a book and place it on a shelf, you exert an upward force against gravity. This force increases the book’s gravitational potential energy, which depends on the book’s height and mass. If the book falls, the potential energy converts into kinetic energy.
Example 2: Elastic Potential Energy in a Stretched Spring
Stretching a spring requires applying a force that pulls its coils apart. The force used to stretch the spring is stored as elastic potential energy. When you release the spring, this stored energy converts back into kinetic energy, causing the spring to return to its original shape.
Example 3: Electrical Potential Energy in a Charged Particle
When a charged particle, like an electron, is moved within an electric field, a force is applied to move it from one point to another. This force alters the particle’s electrical potential energy, which depends on its position in the field. If the particle is released, the energy can convert into kinetic energy, causing the particle to move.
Example 4: Potential Energy of Water in a Dam
Water stored behind a dam has gravitational potential energy due to its elevated position. The force of gravity acting on the water increases this potential energy. When the water is released, the potential energy converts into kinetic energy, driving turbines to generate electricity.
Example 5: Chemical Potential Energy in a Compressed Gas
Compressing a gas within a cylinder involves applying force to reduce the gas volume. This force increases the gas’s chemical potential energy, which is stored in the compressed state. When the gas is allowed to expand, this energy can be converted into mechanical work, such as moving a piston.
Multiple Choice Questions
Question 1
Which of the following correctly describes the relationship between potential energy and the height of an object above the ground?
A) Potential energy decreases as height increases.
B) Potential energy increases as height increases.
C) Potential energy remains constant regardless of height.
D) Potential energy is independent of both height and mass.
Answer: B) Potential energy increases as height increases.
Explanation: Potential energy, specifically gravitational potential energy, is directly related to the height of an object above a reference point (usually the ground). The gravitational potential energy (U) is given by the formula:
U = mgh
Where:
- m is the mass of the object,
- g is the acceleration due to gravity (approximately 9.8 m/s2 on Earth),
- h is the height above the reference point.
As height (h) increases, the potential energy (U) also increases, making option B correct.
Question 2
A spring is compressed by a force F and stores potential energy U. What will happen to the stored potential energy if the force applied to compress the spring is doubled?
A) The stored potential energy doubles.
B) The stored potential energy quadruples.
C) The stored potential energy remains the same.
D) The stored potential energy decreases.
Answer: B) The stored potential energy quadruples.
Explanation: The potential energy stored in a compressed spring is given by Hooke’s Law:
![]()
Where:
- U is the potential energy,
- k is the spring constant,
- x is the displacement from the spring’s equilibrium position.
The force F applied to compress the spring is related to the displacement by F=kx. If the force is doubled, the displacement x is also doubled. Since the potential energy U depends on the square of the displacement (x2), doubling the displacement will result in the potential energy increasing by a factor of four (quadrupling).
Question 3
Which of the following statements about conservative forces and potential energy is true?
A) A conservative force increases the total mechanical energy of a system.
B) Work done by a conservative force depends on the path taken.
C) Potential energy is associated with non-conservative forces only.
D) The work done by a conservative force on an object is equal to the negative change in potential energy.
Answer: D) The work done by a conservative force on an object is equal to the negative change in potential energy.
Explanation: A conservative force is one for which the work done does not depend on the path taken, only on the initial and final positions. The work (W) done by a conservative force is related to the change in potential energy (ΔU) by:
![]()
This means that if a conservative force does work on an object, it will result in a corresponding decrease in the potential energy of the system, and vice versa. This is the basis for the conservation of mechanical energy in a system with only conservative forces. Therefore, option D is correct.


