Impulse and Momentum

Impulse and momentum are fundamental concepts in AP Physics that describe how objects move and interact. Momentum, defined as the product of an object’s mass and velocity, measures how much motion an object has. Impulse, on the other hand, represents the change in momentum caused by a force acting over time. Understanding these concepts is crucial for analyzing collisions, predicting motion, and applying the principle of conservation of momentum in various physical scenarios, all of which are key topics in AP Physics.

Learning Objectives

By studying Impulse and Momentum for the AP Physics exam, you should aim to master the following objectives: Understand the concept of momentum as a vector quantity, and how it relates to mass and velocity. Grasp the significance of impulse and its relationship to changes in momentum. Learn to apply the Impulse-Momentum Theorem in solving real-world problems. Be able to analyze and solve collision problems using the principle of conservation of momentum, distinguishing between elastic and inelastic collisions.

1.Understanding Momentum

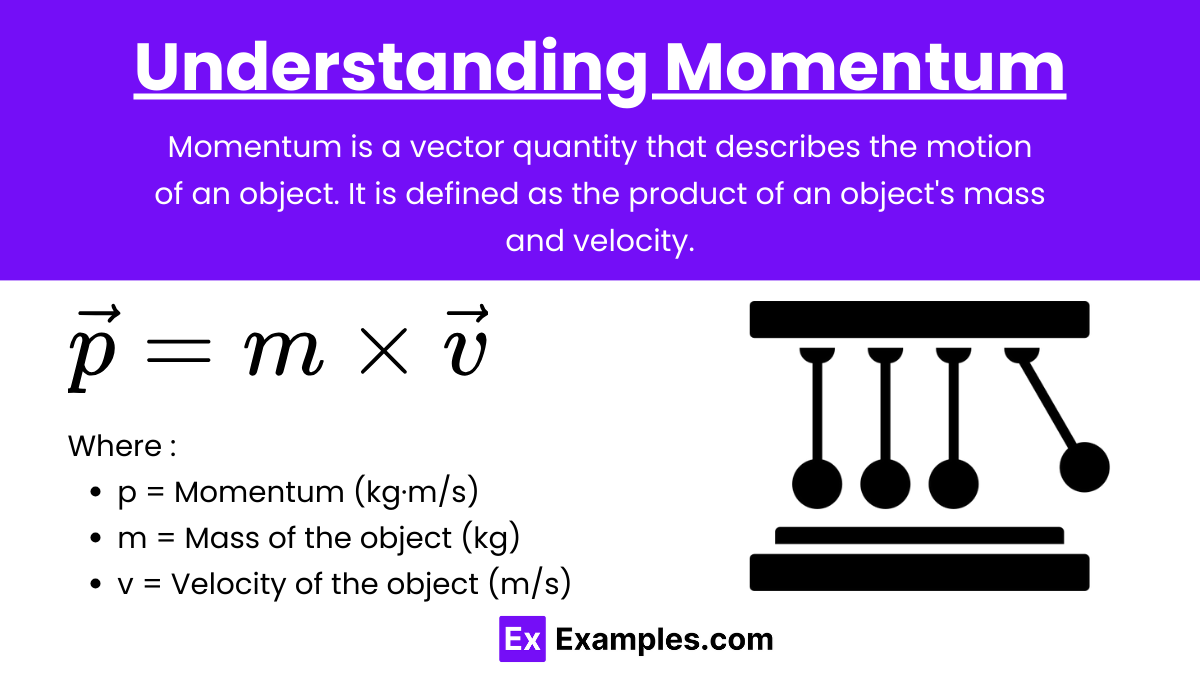
Momentum is a vector quantity that describes the motion of an object. It is defined as the product of an object’s mass and velocity.

Where:

• p = Momentum (kg·m/s)
• m = Mass of the object (kg)
• v = Velocity of the object (m/s)

Key Points:

• Momentum has both magnitude and direction, making it a vector quantity.
• The direction of momentum is the same as the direction of the object’s velocity.
• In the absence of external forces, the total momentum of a system remains constant (conservation of momentum).

2. Impulse: The Change in Momentum

Impulse is the change in momentum of an object when a force is applied over a specific time interval. It quantifies the effect of a force acting over time on an object’s motion.

Where:

• J = Impulse (N·s or kg·m/s)
• Δp = Change in momentum (kg·m/s)
• F = Average force applied (N)
• Δt = Time interval over which the force is applied (s)

Key Points:

• Impulse is also a vector quantity.
• Impulse can be visualized as the area under a force vs. time graph.
• The longer the time over which a force is applied, the greater the impulse.

3. Impulse-Momentum Theorem

The Impulse-Momentum Theorem states that the impulse on an object is equal to the change in its momentum.

This theorem connects the concepts of impulse and momentum, providing a powerful tool for analyzing collisions and other interactions in physics.

4. Conservation of Momentum

The principle of Conservation of Momentum is a fundamental concept in physics that states that the total momentum of a closed system remains constant if no external forces act on it. This means that the momentum before an interaction (such as a collision or explosion) is equal to the momentum after the interaction. Mathematically, this is expressed as:

p_initial = p_final

Where:

• pinitial​ is the total momentum of the system before the interaction.
• pfinal​ is the total momentum of the system after the interaction.

Elastic and Inelastic Collisions

• Elastic Collisions: Both momentum and kinetic energy are conserved. The objects bounce off each other without any loss of total kinetic energy.
• Example: Two billiard balls colliding.
• Inelastic Collisions: Momentum is conserved, but kinetic energy is not. The objects may stick together after the collision, resulting in some loss of kinetic energy.
• Example: A car crash where the vehicles stick together after impact.

Impulse in Real-World Applications

1. Automotive Safety: Impulse plays a critical role in the design of safety features in vehicles. Airbags, seatbelts, and crumple zones are engineered to extend the time over which the force from a collision is applied to the passengers. By increasing the time duration (Δt\Delta tΔt) of the impact, the force experienced by passengers is reduced, minimizing injury. For example, airbags inflate quickly during a crash to cushion the impact, spreading the force over a larger area and a longer time period.

2. Sports: In sports like baseball, tennis, and soccer, impulse is key to controlling the speed and direction of the ball. Athletes apply a force over a specific time interval to change the ball’s momentum. For instance, a baseball player swings the bat to impart an impulse on the ball, increasing its velocity and sending it in the desired direction. Similarly, in tennis, players use the racket to apply force over time, controlling the ball’s speed and trajectory.

3. Rocket Propulsion: Impulse is fundamental in rocket science. Rockets work on the principle of conservation of momentum. When a rocket expels gas at high speeds, the gas generates an impulse that changes the rocket’s momentum, propelling it forward. The thrust provided by the expelling gases over time results in the acceleration of the rocket, enabling it to overcome gravity and travel through space.

4. Ballistics and Firearms: In firearms, impulse determines the bullet’s velocity as it leaves the barrel. The explosive force inside the gun applies a large force over a very short time, creating a significant impulse that accelerates the bullet. The momentum imparted to the bullet determines its speed and penetration power, while the same impulse applies an equal and opposite force on the gun, resulting in recoil.

5. Everyday Activities: Impulse is also involved in everyday activities, such as catching a ball. When you catch a ball, your hands move backward upon contact to increase the time over which the force is applied, reducing the impact force and preventing injury. Similarly, when jumping onto a surface, bending your knees helps extend the time of impact, reducing the force on your joints.

Examples

Example 1: Hitting a Baseball with a Bat

When a baseball player swings a bat and hits a ball, the bat exerts a force on the ball over a short period of time, changing the ball’s momentum. The impulse delivered by the bat equals the change in the ball’s momentum, causing the ball to accelerate and fly off in a different direction with a higher speed.

Example 2: Car Collision with an Airbag

During a car accident, the momentum of the car and its passengers changes rapidly as they come to a stop. The airbag inflates and increases the time over which the force acts on the passengers, reducing the force experienced by them. This cushioning effect decreases the impact, demonstrating how impulse (force multiplied by time) is used to safely manage the momentum change.

Example 3: Kicking a Soccer Ball

When a player kicks a soccer ball, their foot applies a force over a brief moment, causing a change in the ball’s momentum. The strength and duration of the kick determine the magnitude of the impulse, which directly influences the ball’s speed and direction after the kick.

Example 4: Landing after a Jump

When a person jumps and lands on the ground, their momentum changes as they come to a stop. Bending the knees upon landing increases the time over which the force acts, reducing the impact force. This action minimizes injury and is an example of how impulse can be controlled to manage momentum safely.

Example 5: Bouncing a Basketball

When a basketball hits the ground, it exerts a force on the ground and, in turn, the ground exerts an equal and opposite force on the ball. This force changes the ball’s momentum, causing it to bounce back up. The impulse received from the ground reverses the direction of the ball’s momentum, sending it upwards again.

Multiple Choice Questions

Question 1

Which of the following statements correctly describes the relationship between impulse and momentum?

A) Impulse is the rate of change of momentum.
B) Momentum is the integral of impulse over time.
C) Impulse is the product of force and time, and it equals the change in momentum.
D) Momentum is the product of force and time, and it equals the impulse.

Answer: C) Impulse is the product of force and time, and it equals the change in momentum.

Explanation: Impulse (J) is defined as the product of force (F) and the time (t) over which the force acts:
J = F×t

According to the impulse-momentum theorem, impulse is also equal to the change in momentum (Δp):
J = Δp = mΔv
where m is the mass of the object and Δv is the change in velocity. This means that when a force is applied over a certain time interval, it changes the object’s momentum by an amount equal to the impulse.

Q2: A 2 kg ball is moving at 3 m/s. A force of 4 N is applied in the direction of the ball’s motion for 2 seconds. What is the ball’s final velocity?

A) 5 m/s
B) 7 m/s
C) 9 m/s
D) 11 m/s

Answer: B) 7 m/s

Explanation:
First, calculate the impulse imparted to the ball:
J=F×t=4 N×2 s=8 Ns

Next, use the impulse-momentum theorem to find the change in momentum:
J = Δp = m × Δv
8 Ns=2 kg × Δv

Solve for Δv:
Δv= 8 Ns/ 2 kg= 4 m/s

Now, add this change in velocity to the initial velocity to find the final velocity:
v_final = v_initial+ Δv=3 m/s+4 m/s=7 m/s

Q3: A car of mass 1000 kg is traveling at 20 m/s and comes to a stop in 5 seconds due to the application of brakes. What is the magnitude of the average force applied by the brakes?

A) 4000 N
B) 2000 N
C) 1000 N
D) 500 N

Answer: A) 4000 N

Explanation:
First, calculate the initial momentum of the car:
p_initial = m × v_initial = 1000 kg × 20 m/s = 20000 kg m/s

Since the car comes to a stop, the final momentum is:
p_final = 0 kg m/s

The change in momentum (Δp\Delta pΔp) is therefore:
Δp = p_final−p_initial = 0−20000 kg m/s = −20000 kg m/s

Using the impulse-momentum theorem (J = Δp), and knowing that J =F × t, we can solve for the average force (F):

F × t = Δp
F ×5 s = −20000 kg m/s
F = −20000 kg m/s / 5 s=−4000 N

The magnitude of the force is 4000N. The negative sign indicates that the force is applied in the direction opposite to the car’s motion, which makes sense since the brakes are slowing down the car.