Kinematics in One Dimension

Kinematics in one dimension focuses on the motion of objects along a straight line, providing a foundational understanding of concepts like displacement, velocity, and acceleration. In AP Physics, this topic is crucial as it sets the stage for more complex analyses of motion. By examining how objects move in a single direction, students learn to apply key equations and interpret motion graphs, essential for solving problems in physics. Mastery of these principles is vital for success in AP Physics exams.

Learning Objectives

When studying Kinematics in One Dimension for the AP Physics exam, you should focus on understanding the concepts of displacement, velocity, and acceleration, including how to distinguish between scalar and vector quantities. Master the use of kinematic equations to solve problems involving uniformly accelerated motion. Develop skills in interpreting and creating position-time, velocity-time, and acceleration-time graphs. Additionally, learn to analyze special cases like free fall and motion on inclines, ensuring you can apply these concepts to real-world scenarios and complex problem-solving situations.

Introduction to Kinematics in One Dimension

Kinematics is the branch of mechanics that describes the motion of objects without considering the forces that cause the motion. When we study kinematics in one dimension, we focus on the motion of objects along a straight line, typically described along the x-axis or y-axis.

Key Concepts in One-Dimensional Kinematics

1. Position (x):
   • The position of an object is its location along a straight line relative to a reference point, often called the origin (x = 0).
   • Position can be positive or negative depending on the direction chosen as positive.
2. Displacement (Δx):
   • Displacement is the change in position of an object. It is a vector quantity, which means it has both magnitude and direction.
   • Displacement is calculated as: \( \Delta x = x_{f} – x_{i} \)
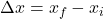
   • where x_f is the final position, and x_i​ is the initial position.
3. Distance:
   • Distance is the total path length traveled by an object, regardless of direction. Unlike displacement, distance is a scalar quantity and is always positive.
4. Velocity (v):
   • Velocity is the rate of change of displacement with respect to time. It is also a vector quantity.
   • Average velocity (v_avg​) is calculated as: \( v_{\text{avg}} = \frac{\Delta x}{\Delta t} \)
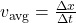
   • ​ whereΔt is the time interval.
   • Instantaneous velocity is the velocity of an object at a specific moment in time, given by the derivative of position with respect to time: \( v(t) = \frac{dx}{dt} \)
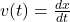
5. Speed:
   • Speed is the rate at which an object covers distance. It is a scalar quantity and does not consider direction.
   • Average speed is calculated as: \( \text{Speed}_{\text{avg}} = \frac{\text{Total Distance}}{\text{Total Time}} \)
     
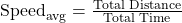
6. Acceleration (a):
   • Acceleration is the rate of change of velocity with respect to time. It is a vector quantity.
   • Average acceleration (a_avg​) is calculated as: \( a_{\text{avg}} = \frac{\Delta v}{\Delta t} \)
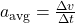
   • Instantaneous acceleration is given by the derivative of velocity with respect to time: \( a(t) = \frac{dv}{dt} \)

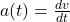
Kinematic Equations for Uniformly Accelerated Motion

In one-dimensional motion with constant acceleration, the following kinematic equations are used:

First Equation of Motion: \( v = v_{0} + at \)

Where v₀ is the initial velocity, v is the final velocity, aaa is the constant acceleration, and t is the time elapsed.

Second Equation of Motion: \( x = x_{0} + v_{0}t + \frac{1}{2}at^{2} \)

Where x₀ is the initial position, and x is the final position.

Third Equation of Motion: \( v^{2} = v_{0}^{2} + 2a(x – x_{0}) \)

This equation relates the final velocity to the initial velocity, acceleration, and displacement.

Displacement Without Time: \( \Delta x = \frac{v + v_{0}}{2}t \)

This equation calculates displacement when time is known, but acceleration is not explicitly used.

Graphical Analysis of Motion

1. Position-Time Graph:
   • A straight line indicates constant velocity (slope = velocity).
   • A curved line indicates changing velocity, hence acceleration.
2. Velocity-Time Graph:
   • The slope of the velocity-time graph gives acceleration.
   • The area under the velocity-time graph gives the displacement.
3. Acceleration-Time Graph:
   • The slope of the acceleration-time graph indicates the change in acceleration (jerk), although it is usually zero in uniform acceleration cases.
   • The area under the acceleration-time graph gives the change in velocity.

Special Cases of One-Dimensional Motion

1. Free Fall:
   • Objects under free fall move under the influence of gravity alone, with acceleration g ≈ 9.8 m/s² downward.
   • In the absence of air resistance, all objects fall at the same rate regardless of mass.
2. Motion on an Incline:
   • Motion on a frictionless incline can be treated as one-dimensional motion with constant acceleration, where the acceleration a is a component of gravitational acceleration: a = gsin⁡θ. θ is the angle of the incline with the horizontal.

Examples

Example 1: A Car Moving on a Straight Road

Imagine a car traveling along a straight highway. If the car accelerates from rest to a certain speed, then continues at that constant speed before decelerating to a stop, this entire motion is an example of kinematics in one dimension. The car’s position changes only along the length of the road, which is the one-dimensional axis of motion.

Example 2: A Ball Dropped from a Height

Consider a ball dropped from the top of a building. As the ball falls straight down, it accelerates due to gravity, which is the only force acting on it (ignoring air resistance). The motion of the ball is purely vertical, making it a classic example of one-dimensional kinematics, where we can analyze the displacement, velocity, and acceleration in the vertical direction.

Example 3: An Object Thrown Straight Up

When you throw a ball straight up into the air, it moves upward until it reaches its peak height and then falls back down. The motion is restricted to a single vertical line. Throughout this journey, the ball’s velocity decreases as it rises, becomes zero at the top, and then increases again as it falls, all within one dimension.

Example 4: A Train Moving Along a Straight Track

Consider a train moving along a straight track from one station to another. As it starts, it accelerates to a certain speed, maintains that speed, and then decelerates as it approaches the next station. The entire motion occurs along a straight path, making it an ideal example of kinematics in one dimension.

Example 5: A Runner on a Straight Path

Imagine a sprinter running on a straight track during a 100-meter dash. The runner accelerates from the starting line, reaches top speed, and then crosses the finish line. The entire motion occurs along a single straight line, which means the analysis of the runner’s motion involves only one-dimensional kinematics.

Multiple Choice Questions

Question 1:

A car moves at a steady speed of 20 m/s for 5 seconds. Then, it speeds up to 40 m/s over the next 5 seconds. What is the total distance the car travels in 10 seconds?

A) 200 meters
B) 300 meters
C) 350 meters
D) 400 meters

Answer: C) 350 meters

Explanation:

1. In the first 5 seconds, the car moves at 20 m/s, so it travels 20×5=100 meters.
2. In the next 5 seconds, the car speeds up. The average speed during this time is 20+40/2=30 m/s. So, it travels 30×5=150 meters.

Total distance: 100+150 = 250 meters.

So, the car travels 350 meters in total.

Question 2:

A ball is thrown straight up with a speed of 15 m/s. What is the highest point it reaches? (Assume gravity g=9.8 m/s²).

A) 7.5 meters
B) 11.5 meters
C) 15.5 meters
D) 22.5 meters

Answer: B) 11.5 meters

Explanation:

The ball will slow down as it goes up because of gravity. At its highest point, its speed will be 0. Using the formula for height:

\( \text{Height} = \frac{(10)^{2}}{2 \times 9.8} \approx 11.5 \text{ meters} \)

So, the ball reaches 11.5 meters high.

Question 3:

Which of the following is true about an object moving with constant acceleration?

A) The object’s speed stays the same.
B) The object’s position changes in a straight line over time.
C) The object’s speed changes by the same amount each second.
D) The object’s acceleration increases over time.

Answer: C) The object’s speed changes by the same amount each second.

Explanation:

• Option A is wrong because with constant acceleration, speed changes.
• Option B is wrong because the distance covered doesn’t increase in a straight line but curves upwards.
• Option C is correct because, with constant acceleration, speed increases steadily.
• Option D is wrong because acceleration doesn’t change—it stays the same.

So, C) The object’s speed changes by the same amount each second is the right answer.