Kinematics in Two Dimensions

Kinematics in Two Dimensions involves the study of motion in a plane, considering both horizontal and vertical components. Unlike one-dimensional motion, it requires analyzing vector quantities such as displacement, velocity, and acceleration in both the x and y directions. In AP Physics, understanding this concept is crucial as it forms the foundation for topics like projectile motion and circular motion. Mastery of two-dimensional kinematics is essential for solving complex real-world problems involving motion in multiple directions.

Free AP Physics C: Mechanics Practice Test

Learning Objectives

By studying Kinematics in Two Dimensions for the AP Physics exam, you should learn to analyze motion in the xy-plane using vector components, understand and apply equations of motion separately for horizontal and vertical directions, and solve complex problems involving projectile motion. You should also grasp the concept of relative velocity in two dimensions and be able to decompose and recombine vectors effectively. Mastering these objectives will enable you to tackle a wide range of physics problems involving two-dimensional motion.

Understanding Two-Dimensional Motion

Two-dimensional motion occurs when an object moves in a plane, having both horizontal (x) and vertical (y) components. Unlike one-dimensional motion, where motion is confined to a single axis, two-dimensional motion requires analyzing both axes simultaneously.

Key Components:

1. Displacement, Velocity, and Acceleration in Two Dimensions

Displacement

Displacement is a vector that points from the initial position to the final position of an object.
Formula: \( \vec{d} = \sqrt{(x_{f} – x_{i})^{2} + (y_{f} – y_{i})^{2}} \)
where d is the displacement vector, and (x_f,y_f) and (x_i,y_i) are the final and initial positions in the xy-plane, respectively.

Velocity

Velocity in two dimensions is a vector quantity that describes the rate of change of displacement.
Components: \( \vec{v} = v_{x} \hat{i} + v_{y} \hat{j} \)
where v_x and v_y are the velocity components in the x and y directions, respectively.
Magnitude of Velocity (Speed): \( v = \sqrt{v_{x}^{2} + v_{y}^{2}} \)
Direction: \( \theta = \tan^{-1} \left( \frac{v_{y}}{v_{x}} \right) \)

Acceleration

Definition: Acceleration is a vector quantity that represents the rate of change of velocity with time.
Components: \( \vec{a} = a_{x} \hat{i} + a_{y} \hat{j} \)
Where a_xand a_y are the acceleration components in the x and y directions, respectively.
Magnitude of Acceleration: \( a = \sqrt{a_{x}^{2} + a_{y}^{2}} \)
Direction: \( \theta_{a} = \tan^{-1} \left( \frac{a_{y}}{a_{x}} \right) \)

2. Equations of Motion in Two Dimensions

The equations of motion in two dimensions are derived from one-dimensional kinematics, applied separately to each axis.

For the X-axis:

\( x_{f} = x_{i} + v_{xi}t + \frac{1}{2}a_{x}t^{2} \)
\[ v_{xf} = v_{xi} + a_{x}t \]
\[ v_{xf}^{2} = v_{xi}^{2} + 2a_{x}(x_{f} – x_{i}) \]

For the Y-axis:

\[ y_{f} = y_{i} + v_{yi}t + \frac{1}{2}a_{y}t^{2} \]
\[ v_{yf} = v_{yi} + a_{y}t \]
\[ v_{yf}^{2} = v_{yi}^{2} + 2a_{y}(y_{f} – y_{i}) \]

Note: t (time) is the same for both axes because time is a scalar and does not depend on direction.

3. Projectile Motion

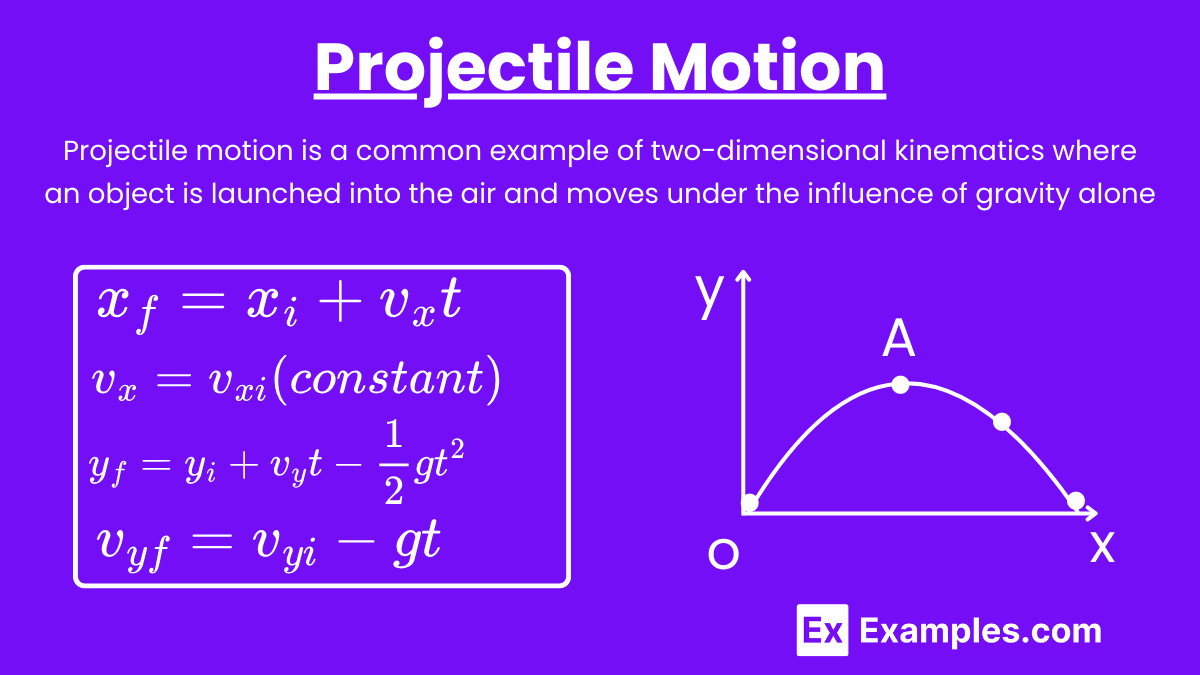
Projectile motion is a common example of two-dimensional kinematics where an object is launched into the air and moves under the influence of gravity alone.

Assumptions:
- Acceleration in the x-direction, a_x=0, as there is no horizontal acceleration (ignoring air resistance).
- Acceleration in the y-direction, a_y=−g, where ggg is the acceleration due to gravity (approximately 9.8 m/s² downward).

Key Equations in Projectile Motion:

Horizontal Motion (X-axis):
\( x_{f} = x_{i} + v_{x} t \)
\( v_{x} = v_{xi} \) (constant)
Vertical Motion (Y-axis):
\( y_{f} = y_{i} + v_{y} t – \frac{1}{2} g t^{2} \)
\( v_{yf} = v_{yi} – g t \)

Range of Projectile:

The range R is the horizontal distance the projectile travels. \( R = \frac{v_{i}^{2} \sin 2\theta}{g} \)
where v_i is the initial velocity and θ is the launch angle.

Maximum Height:

The maximum height H reached by the projectile: \( H = \frac{v_{i}^{2} \sin^{2} \theta}{2g} \)

Time of Flight:

The time of flight T is the total time the projectile remains in the air. \( T = \frac{2v_{i} \sin \theta}{g} \)

4. Relative Motion in Two Dimensions

Relative motion involves determining the velocity of an object as observed from a different frame of reference. In two dimensions, this requires vector addition.

Relative Velocity Formula: \( \vec{v}_{A/B} = \vec{v}_{A} – \vec{v}_{B} \) where v_A/B is the velocity of object A relative to object B, vA is the velocity of object A, and vB is the velocity of object B.

Examples

Example 1: Projectile Motion of a Soccer Ball

Imagine a soccer player kicking a ball into the air. The ball follows a curved path, known as a parabolic trajectory. The motion in the horizontal direction remains constant, while the vertical motion is influenced by gravity. As a result, the ball first rises, reaches a peak height, and then falls back to the ground. This classic example of two-dimensional kinematics involves both horizontal and vertical components that can be analyzed separately using kinematic equations.

Example 2: Motion of a Car on a Curved Road

Consider a car driving along a curved road. The car’s velocity changes direction as it follows the curve, even if its speed remains constant. This change in direction involves two-dimensional motion, as the car has both a forward motion and a lateral motion as it turns. Analyzing this situation requires understanding the vector nature of velocity and acceleration in two dimensions, which are crucial in determining the car’s path and dynamics on the curve.

Example 3: Flight Path of an Airplane

When an airplane takes off and climbs at an angle, it exhibits two-dimensional motion. The airplane moves horizontally while simultaneously gaining altitude. This motion can be broken down into horizontal and vertical components. By analyzing these components separately, we can determine the plane’s overall trajectory, speed, and the effect of external forces like wind resistance and gravity on its path.

Example 4: Riverboat Crossing a River

A riverboat crossing a river with a current presents a classic example of two-dimensional kinematics. As the boat moves across the river, the current pushes it downstream, resulting in a diagonal path. The boat’s velocity relative to the water and the river current must be considered together to determine the boat’s actual path and the time it will take to reach the opposite shore.

Example 5: Satellite Orbiting the Earth

A satellite in orbit around Earth experiences two-dimensional motion as it moves in a circular or elliptical path. The satellite’s motion is influenced by Earth’s gravity, which provides the necessary centripetal force to keep it in orbit. The satellite’s velocity has both a tangential component (along the orbit) and a radial component (due to the gravitational pull). Understanding this motion requires applying the principles of two-dimensional kinematics, particularly in analyzing the balance between gravitational force and the satellite’s inertia.

Multiple Choice Questions

Question 1

A projectile is launched with an initial velocity of 20 m/s at an angle of 30^∘ above the horizontal. What is the horizontal component of the initial velocity?

A) 10 m/s
B) 17.3 m/s
C) 20 m/s
D) 30 m/s

Correct Answer: B) 17.3 m/s

Explanation: To find the horizontal component of the initial velocity, we use the formula:

\( v_{x} = v_{0} \cdot \cos(\theta) \)

where v₀ is the initial velocity and θ is the angle of projection.

Given:

v₀=20 m/s
θ=30∘

Substituting the values:

\( v_{x} = 20 \, \text{m/s} \cdot \cos(30^\circ) \)
\( v_{x} = 20 \, \text{m/s} \cdot \frac{\sqrt{3}}{2} \approx 17.3 \, \text{m/s} \)

Thus, the horizontal component of the initial velocity is approximately 17.3 m/s.

Question 2

A soccer ball is kicked horizontally off a cliff that is 45 meters high with a speed of 10 m/s. How long does it take for the ball to hit the ground? (Assume g=9.8 m/s²)

A) 1.0 s
B) 2.0 s
C) 3.0 s
D) 4.0 s

Correct Answer: C) 3.0 s

Explanation: The time taken for the ball to hit the ground depends on the vertical motion, which is independent of the horizontal motion. We use the following kinematic equation for vertical displacement:

\( y = \frac{1}{2} g t^{2} \)

Given:

y = 45m
g = 9.8 m/s²

Rearranging the equation to solve for time t:

\( t^{2} = \frac{2y}{g} = \frac{2 \times 45 \, \text{m}}{9.8 \, \text{m/s}^2} \approx 9.18 \, \text{s}^{2} \)

\( t = \sqrt{9.18} \approx 3.0 \, \text{s} \)

Therefore, the ball takes 3.0 seconds to hit the ground.

Question 3

If a car travels along a curved path with a constant speed of 15 m/s, which of the following is true about the car’s acceleration?

A) The car has no acceleration.
B) The car has only tangential acceleration.
C) The car has only centripetal acceleration.
D) The car has both tangential and centripetal acceleration.

Correct Answer: C) The car has only centripetal acceleration.

Explanation: When an object moves along a curved path at a constant speed, its velocity vector changes direction, but not magnitude. The change in direction of the velocity vector means that the object is accelerating, even though the speed is constant. This acceleration, which is always directed towards the center of the curvature of the path, is called centripetal acceleration.

Since the speed is constant, there is no change in the magnitude of velocity, so there is no tangential acceleration. Thus, the car experiences only centripetal acceleration.