Rotational Dynamics and Energy

Rotational Dynamics and Energy extend the principles of linear motion to rotating systems, exploring how objects spin, roll, and resist changes in their rotation. Key concepts include torque, moment of inertia, angular momentum, and rotational kinetic energy. These topics are crucial for understanding the behavior of rotating bodies, such as wheels and planets, in various physical situations. Mastering these concepts is essential for solving complex problems in AP Physics, as they are frequently tested and integral to a deeper comprehension of mechanics.

Free AP Physics C: Mechanics Practice Test

Learning Objectives

By studying Rotational Dynamics and Energy for the AP Physics exam, you should aim to understand the principles of rotational motion, including angular velocity, angular acceleration, and torque. You should be able to apply the concepts of moment of inertia, rotational kinetic energy, and angular momentum in various contexts. Master the ability to solve problems involving rolling motion, rotational equilibrium, and energy conservation in rotating systems. Additionally, focus on using the conservation of angular momentum to analyze rotational dynamics effectively.

Introduction to Rotational Dynamics

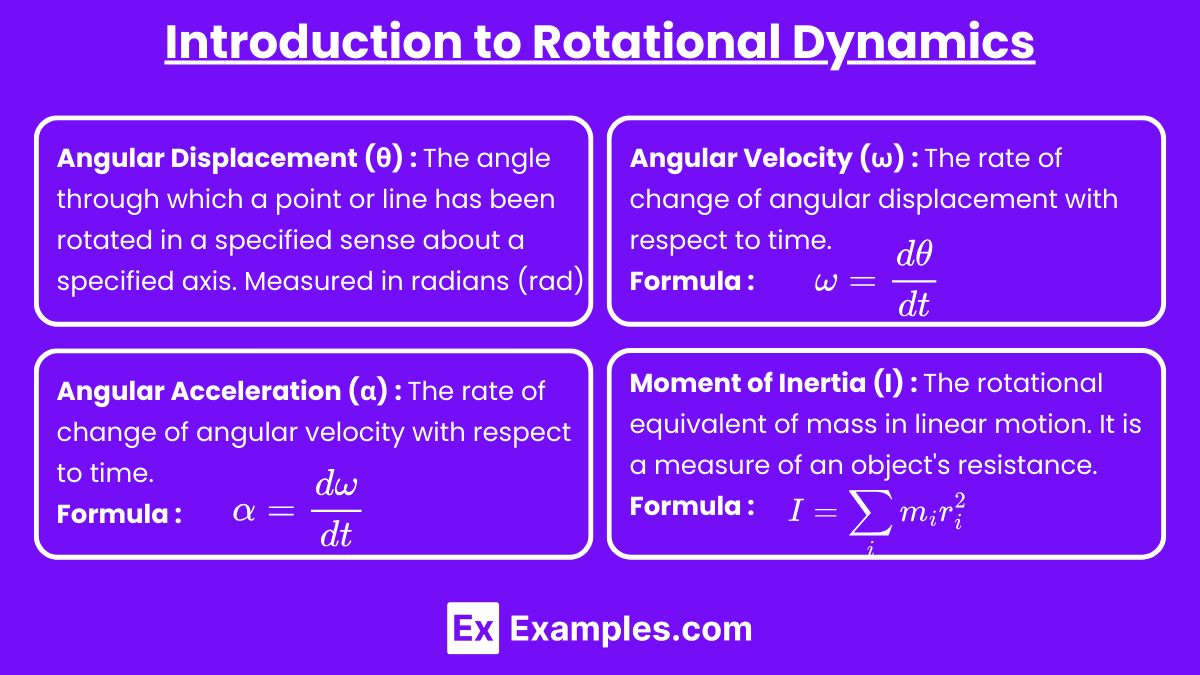
Rotational Dynamics deals with the motion of objects that rotate about an axis. It is analogous to linear dynamics but with quantities like torque, angular momentum, and moment of inertia replacing force, momentum, and mass.

Key Quantities in Rotational Motion

Angular Displacement (θ):
- The angle through which a point or line has been rotated in a specified sense about a specified axis.
- Measured in radians (rad).
Angular Velocity (ω):
- The rate of change of angular displacement with respect to time.
- \( \omega = \frac{d\theta}{dt} \)
- Measured in radians per second (rad/s).
Angular Acceleration (α):
- The rate of change of angular velocity with respect to time.
- \( \alpha = \frac{d\omega}{dt} \)
- Measured in radians per second squared (rad/s²).
Moment of Inertia (I):
- The rotational equivalent of mass in linear motion.
- It is a measure of an object’s resistance to changes in its rotational motion.
- \( I = \sum m_{i} r_{i}^{2} \)
- where:
- m_i is the mass of the iii-th particle.
- r_i is the perpendicular distance of the iii-th particle from the axis of rotation.
- For a point mass, \( I = m \times (r^{2}) \), where m is mass and r is the distance from the axis of rotation.
- For continuous bodies, \( I = \int (r^{2}) \, dm \).

Rotational Kinematics Equations

These equations are similar to the kinematic equations for linear motion but apply to rotational quantities:

\( \omega_{f} = \omega_{i} + (\alpha \times t) \)
\( \theta = (\omega_{i} \times t) + \frac{1}{2} \times (\alpha \times t^{2}) \)
\( \omega_{f}^{2} = \omega_{i}^{2} + 2 \times (\alpha \times \theta) \)

Where:

ω_i is the initial angular velocity,
ω_f is the final angular velocity,
α is the angular acceleration,
t is the time, and
θ is the angular displacement.

Torque and Its Effects

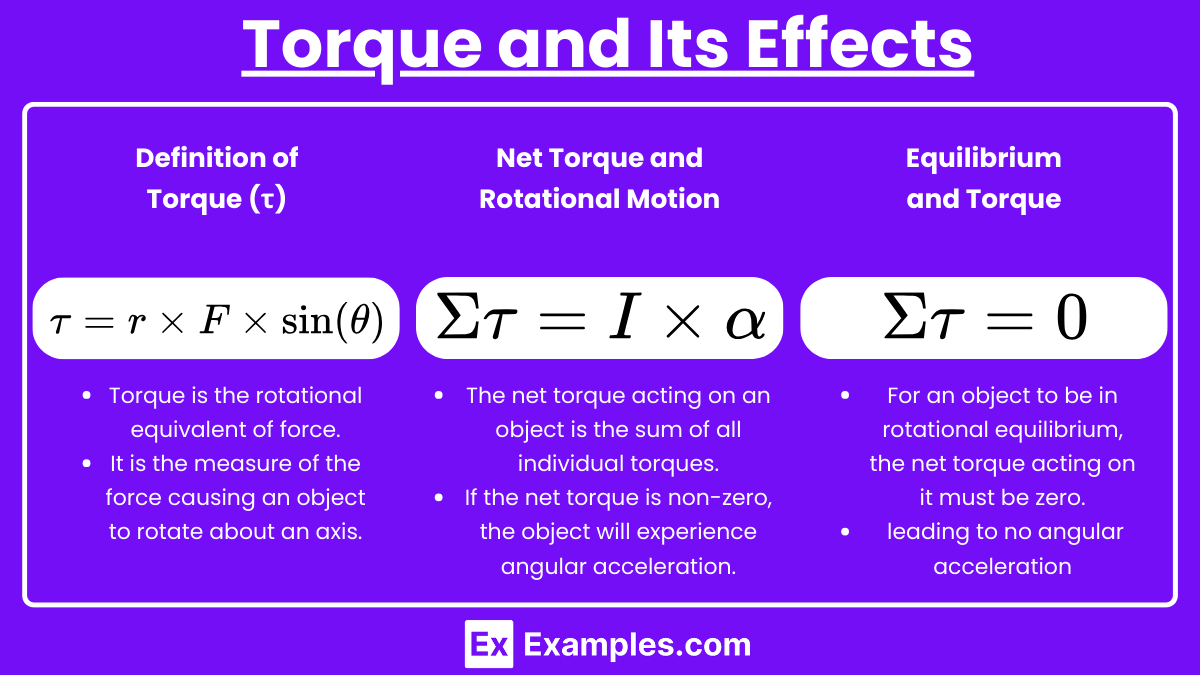
Definition of Torque (τ):

Torque is the rotational equivalent of force.
It is the measure of the force causing an object to rotate about an axis.
\( \tau = r \times F \times \sin(\theta) \), where:
- r is the lever arm (distance from the axis of rotation to the point where the force is applied),
- F is the force applied,
- θ is the angle between the force vector and the lever arm.

Net Torque and Rotational Motion:

The net torque acting on an object is the sum of all individual torques.
If the net torque is non-zero, the object will experience angular acceleration.
\( \Sigma \tau = I \times \alpha \)

Equilibrium and Torque:

For an object to be in rotational equilibrium, the net torque acting on it must be zero.
This means \( \Sigma \tau = 0 \), leading to no angular acceleration.

Rotational Energy

Rotational Kinetic Energy (K_rot):

Just as linear motion involves kinetic energy, rotational motion has its own form of kinetic energy.
\( K_{rot} = \frac{1}{2} \times I \times \omega^{2} \)
This equation shows that rotational kinetic energy depends on the moment of inertia and the square of the angular velocity.

Conservation of Energy in Rotational Motion:

In a closed system, the total mechanical energy (sum of kinetic and potential energies) is conserved.
If a body is both rotating and translating, the total kinetic energy is the sum of translational and rotational kinetic energies:
- \( K_{total} = \frac{1}{2} \times m \times v^{2} + \frac{1}{2} \times I \times \omega^{2} \)

Angular Momentum (L)

Definition of Angular Momentum:

Angular momentum is the rotational equivalent of linear momentum.
\( L = I \times \omega \)
For a system of particles, \( L = \Sigma (r_{i} \times p_{i}) \), where p_i is the linear momentum of the i^th particle.

Conservation of Angular Momentum:

In the absence of an external torque, the total angular momentum of a system remains constant.
\( I_{1} \times \omega_{1} = I_{2} \times \omega_{2} \)
This principle is often observed in systems like figure skaters pulling in their arms to spin faster.

Rotational Dynamics in Rigid Bodies

Rigid Body Rotation:

A rigid body is an object with a mass that does not deform under the action of forces.
Every point in a rigid body has the same angular velocity and angular acceleration.

Rolling Motion:

Rolling motion is a combination of rotational and translational motion.
For a wheel rolling without slipping, the condition v=ωr applies, where v is the linear speed of the center of mass, and r is the radius of the wheel.

Energy in Rolling Motion:

Total kinetic energy for a rolling object is the sum of translational and rotational kinetic energies: \( K_{total} = \frac{1}{2}mv^{2} + \frac{1}{2}I\omega^{2} \)
For a uniform solid sphere, \( I = \frac{2}{5}mr^{2} \), and for a cylinder, \( I = \frac{1}{2}mr^{2} \).

Examples

Example 1: Spinning Bicycle Wheel

When you spin a bicycle wheel, it demonstrates several concepts of rotational dynamics and energy. The wheel has angular velocity, which is the rate at which it rotates around its axis. The faster you spin the wheel, the greater its angular velocity. Additionally, the wheel possesses rotational kinetic energy, which depends on its moment of inertia and angular velocity. When you stop applying force to the wheel, friction causes it to decelerate, converting its rotational kinetic energy into thermal energy.

Example 2: Figure Skater’s Spin

A classic example of rotational dynamics is a figure skater performing a spin. When the skater pulls their arms in close to their body, their moment of inertia decreases. To conserve angular momentum, the skater’s angular velocity increases, causing them to spin faster. Conversely, when the skater extends their arms, their moment of inertia increases, and their spin slows down. This demonstrates the conservation of angular momentum and the relationship between moment of inertia and rotational speed.

Example 3: Rotating Space Station

In a rotating space station, artificial gravity can be created using rotational dynamics. As the station rotates, objects and people inside experience a centrifugal force that simulates the effect of gravity. The rotational kinetic energy of the station is a function of its angular velocity and moment of inertia. By adjusting the station’s rotational speed, engineers can control the level of artificial gravity, demonstrating the practical application of rotational dynamics and energy in space exploration.

Example 4: Car’s Flywheel

A flywheel in a car engine is a prime example of rotational energy storage. As the engine runs, the flywheel spins, storing rotational kinetic energy. This energy helps to smooth out the power delivery of the engine by maintaining momentum between combustion cycles. The flywheel’s moment of inertia and rotational speed determine how much energy it can store. This stored energy is crucial for the engine’s efficiency and performance, showcasing the importance of rotational dynamics in automotive engineering.

Example 5: Earth’s Rotation

The Earth’s rotation on its axis is a natural example of rotational dynamics. The planet has an angular velocity that determines the length of a day. Additionally, the Earth has a significant amount of rotational kinetic energy due to its large mass and speed of rotation. This energy plays a role in various geophysical processes, such as the Coriolis effect, which influences weather patterns. The conservation of angular momentum is also evident in how the Earth’s rotation gradually slows down over time due to tidal forces, which is a long-term example of rotational dynamics at work.

Multiple Choice Questions

Question 1

A uniform disk of mass M and radius R is rotating with an angular velocity ω about its central axis. What is the rotational kinetic energy of the disk?

A) \( \frac{1}{4}MR^{2}\omega^{2} \)
B) \( \frac{1}{2}MR^{2}\omega^{2} \)
C) \( \frac{1}{8}MR^{2}\omega^{2} \)
D) \( \frac{1}{2}I\omega^{2} \)

Answer: D) \( \frac{1}{2}I\omega^{2} \)

Explanation:
The rotational kinetic energy of a rotating object is given by the formula:

\( K_{rot} = \frac{1}{2}I\omega^{2} \)

where III is the moment of inertia of the object about the axis of rotation, and ω\omegaω is the angular velocity. For a uniform disk rotating about its central axis, the moment of inertia I is \[ \frac{1}{2}MR^{2} \]. Substituting this into the formula for rotational kinetic energy:

\( K_{rot} = \frac{1}{2}\left(\frac{1}{2}MR^{2}\right)\omega^{2} = \frac{1}{4}MR^{2}\omega^{2} \)

This expression corresponds to choice D when substituting III directly, not expanding further. Therefore, the correct answer is \( \frac{1}{2}I\omega^{2} \) .

Question 2

Which of the following quantities is not a factor in determining the rotational kinetic energy of a rigid body?

A) Moment of inertia
B) Angular velocity
C) Mass
D) Linear velocity

Answer: D) Linear velocity

Explanation:
The rotational kinetic energy of a rigid body is given by:

\( K_{rot} = \frac{1}{2}I\omega^{2} \)

Where:

I is the moment of inertia (depends on mass and distribution of mass).
ω is the angular velocity.

From this formula, it’s clear that moment of inertia and angular velocity are direct factors in determining rotational kinetic energy. Mass is indirectly a factor because it contributes to the moment of inertia. However, linear velocity does not directly affect rotational kinetic energy; it is associated with translational kinetic energy instead.

Therefore, the correct answer is D) Linear velocity.

Question 3

A torque τ is applied to a rigid body, causing an angular acceleration α. If the moment of inertia I of the body is doubled while keeping the torque constant, what will happen to the angular acceleration?

A) It will remain the same.
B) It will double.
C) It will be halved.
D) It will be quadrupled.

Answer: C) It will be halved.

Explanation:
The relationship between torque τ, moment of inertia I, and angular acceleration α is given by:

\( \tau = I \alpha \)

Rearranging this equation to solve for angular acceleration α:

\( \alpha = \frac{\tau}{I} \)

If the moment of inertia III is doubled while keeping the torque τ constant, the angular acceleration α will become:

\( \alpha’ = \frac{\tau}{2I} = \frac{1}{2} \alpha \)

Therefore, the angular acceleration will be halved, making option C the correct answer.