Rotational Kinematics
Rotational kinematics is a fundamental topic in AP Physics that deals with the motion of objects rotating around a fixed axis. It describes how angular displacement, angular velocity, and angular acceleration change over time, analogous to linear kinematics in translational motion. Understanding rotational kinematics is essential for solving problems involving rotating systems, such as wheels, planets, and gears. Mastery of this topic provides a strong foundation for more complex concepts like rotational dynamics and angular momentum in the AP Physics curriculum.
Learning Objectives
In studying Rotational Kinematics for the AP Physics exam, you should focus on understanding the relationships between angular displacement, angular velocity, and angular acceleration. Learn how to apply the key equations of rotational motion under constant angular acceleration, and how to relate linear and rotational quantities, such as displacement, velocity, and acceleration. You should also be able to interpret and analyze rotational motion graphs, solve real-world rotational motion problems, and understand the concept of centripetal acceleration in circular motion.
Introduction to Rotational Kinematics
Rotational kinematics is the branch of mechanics that describes the motion of rotating objects. It is analogous to linear kinematics, but instead of dealing with linear displacement, velocity, and acceleration, rotational kinematics deals with angular displacement, angular velocity, and angular acceleration.
Understanding rotational kinematics is crucial for the AP Physics exam as it lays the foundation for more advanced topics like rotational dynamics and angular momentum.
Key Concepts in Rotational Kinematics
- Angular Displacement (θ)
- Angular displacement is the angle through which an object rotates about a fixed axis. It is the rotational equivalent of linear displacement.
- Unit: Radians (rad), though degrees are sometimes used.
- Formula: 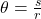\( \theta = \frac{s}{r} \) , where s is the arc length and r is the radius of the circle.
- Angular Velocity (ω)
- Angular velocity is the rate of change of angular displacement with respect to time. It tells us how fast an object is rotating.
- Unit: Radians per second (rad/s).
- Formula:\( \omega = \frac{d\theta}{dt} \)
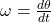
- Average Angular Velocity: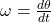\( \omega = \frac{d\theta}{dt} \) , where Δθ is the change in angular displacement and Δt is the change in time.
- Angular Acceleration (α)
- Angular acceleration is the rate of change of angular velocity with respect to time.
- Unit: Radians per second squared (rad/s²).
- Formula: \( \alpha = \frac{d\omega}{dt} \).
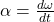- Average Angular Acceleration: 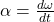\( \alpha = \frac{d\omega}{dt} \), where Δω is the change in angular velocity.
Equations of Rotational Kinematics
Just as in linear kinematics, there are a set of equations that describe the rotational motion of an object under constant angular acceleration:
- First Equation (Angular Velocity-Displacement Relationship) \( \omega_f = \omega_i + \alpha t \)
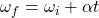
- Second Equation (Angular Displacement-Time Relationship) \( \theta = \omega_i t + \frac{1}{2} \alpha t^2 \)
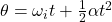
- θ = angular displacement
- ωi = initial angular velocity
- t = time
- α = angular acceleration
- Third Equation (Angular Velocity-Displacement Relationship) \( \omega_f^2 = \omega_i^2 + 2\alpha \theta \)
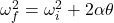
- ωf = final angular velocity
- ωi = initial angular velocity
- α = angular acceleration
- θ = angular displacement
- t = time
Relationship Between Linear and Rotational Quantities
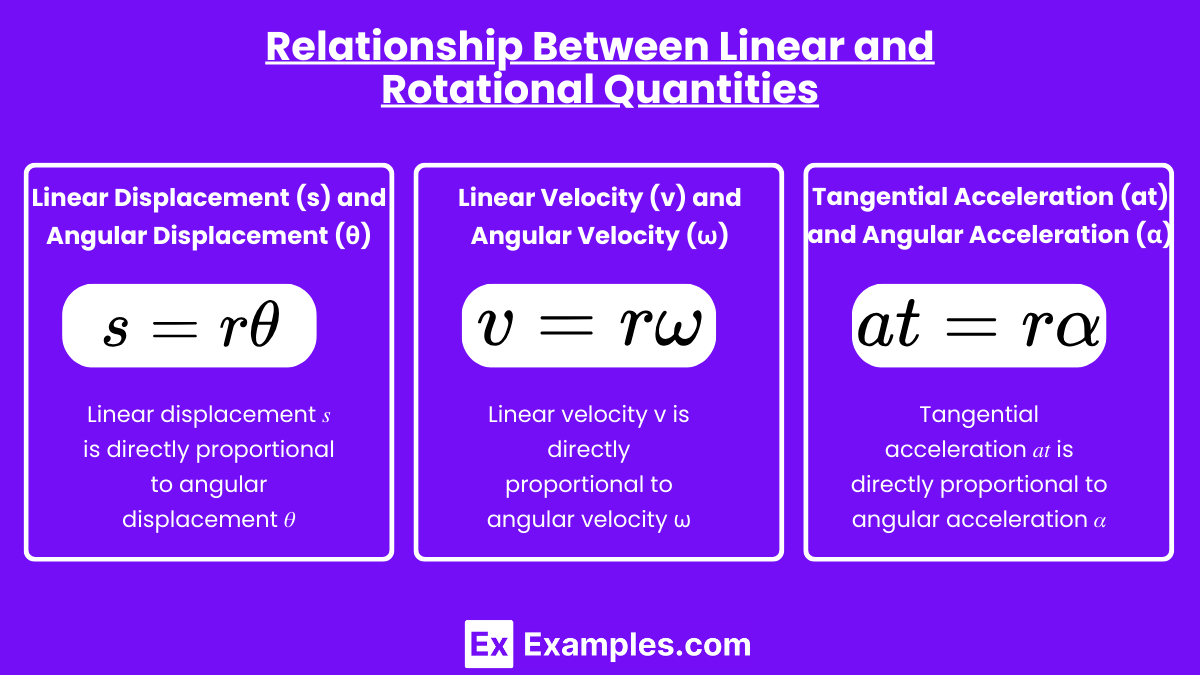
The relationship between linear and rotational quantities in circular motion is expressed through the radius of the circular path r. These relationships are crucial for understanding how linear motion translates into rotational motion.
Linear Displacement (s) and Angular Displacement (θ): s=rθ
Relation: Linear displacement 𝑠 is directly proportional to angular displacement 𝜃. For a given angular displacement, a larger radius results in a greater linear displacement.
Linear Velocity (v) and Angular Velocity (ω): v=rω
Relation: Linear velocity v is directly proportional to angular velocity ω. Points farther from the axis (larger r) move faster in linear terms for the same angular velocity.
Tangential Acceleration (at) and Angular Acceleration (α): at = rα
Relation: Tangential acceleration 𝑎𝑡 is directly proportional to angular acceleration 𝛼. For a given angular acceleration, a larger radius results in a greater tangential acceleration.
Examples
Example 1: Spinning Bicycle Wheel
When a cyclist pedals, the bicycle wheel undergoes rotational motion. The speed at which the wheel rotates, the angular acceleration when the cyclist starts or stops pedaling, and the angle through which the wheel rotates as it completes turns are all described by rotational kinematics.
Example 2: Earth’s Rotation
The Earth rotates around its axis once every 24 hours, which defines the day-night cycle. The angular velocity of the Earth’s rotation is consistent, but during long periods, such as thousands of years, slight changes in angular velocity and precession of the axis can occur, all of which are analyzed using rotational kinematics.
Example 3: Ferris Wheel
A Ferris wheel at an amusement park rotates at a steady rate, giving riders a circular motion experience. The angular velocity of the Ferris wheel is constant if it moves at a uniform rate, and the angular displacement is determined by how many complete rotations the wheel makes.
Example 4: Figure Skater’s Spin
When a figure skater pulls their arms in while spinning, they decrease their moment of inertia and increase their angular velocity due to the conservation of angular momentum. The changes in their spin rate and the angular displacement during the spin can be studied using the principles of rotational kinematics.
Example 5: CD or DVD Player
When a CD or DVD spins inside a player, the disc undergoes rotational motion. The angular velocity may change as the disc moves from the outer edge to the inner part of the disc, where the data is read. The angular acceleration and displacement of the disc are described by rotational kinematics, especially as the player adjusts speed to maintain a constant data read rate.
Multiple Choice Questions
Question 1
A wheel starts from rest and accelerates uniformly at 4 rad/s2. What is its angular velocity after 5 seconds?
A) 10 rad/s
B) 20 rad/s
C) 15 rad/s
D) 25 rad/s
Answer: B) 20 rad/s
Explanation: To find the angular velocity (ω) after a certain time when an object accelerates uniformly, we use the equation:
ω=ω0+αt
Here, ω0 = 0 rad/s (since the wheel starts from rest), α=4 rad/s2, and t=5 seconds.
Substituting the values:
ω=0+(4×5)=20 rad/s
So, the angular velocity after 5 seconds is 20 rad/s.
Question 2:
A disk rotates with an initial angular velocity of 6 rad/s and decelerates uniformly to rest in 3 seconds. What is the magnitude of its angular acceleration?
A) 1 rad/s2
B) 2 rad/s2
C) 3 rad/s2
D) 4 rad/s2
Answer: C) 2 rad/s2
Explanation: The angular acceleration (α) can be calculated using the formula:
α = ω−ω0/ t
Since the disk comes to rest, ω=0 rad/s, ω0=6 rad/s, and t=3 secondst = 3 \, \text{seconds}t=3seconds.
Substituting the values:
α = 0−6/3=−2 rad/s2
The magnitude of the angular acceleration is 2 rad/s2.
Question 3
A point on the rim of a rotating wheel has a tangential speed of 10 m/s10. If the radius of the wheel is 0.5 m, what is the angular speed of the wheel?
A) 5 rad/s
B) 10 rad/s
C) 15 rad/s
D) 20 rad/s
Answer: A) 20 rad/s
Explanation: The relationship between tangential speed (v) and angular speed (ω) is given by:
v = ωrv = ωr
Where v = 10 m/s and r = 0.5 m.
Rearranging the equation to solve for ω:
ω = vr = 10 / 0.5 = 20 rad/s
So, the angular speed of the wheel is 20 rad/s.