Simple Harmonic Motion, Springs, and Pendulums

Last Updated: September 23, 2024

Notes

Simple Harmonic Motion (SHM) is a fundamental concept in AP Physics, describing the oscillatory motion of objects where the restoring force is proportional to the displacement. This concept is critical for understanding systems like springs and pendulums, which are often explored in AP Physics. These systems demonstrate periodic motion, energy conservation, and resonance, making them essential for mastering the subject. A solid grasp of SHM, springs, and pendulums is crucial for success in the AP Physics exam.

Free AP Physics C: Mechanics Practice Test

Learning Objectives

When studying Simple Harmonic Motion, Springs, and Pendulums for the AP Physics exam, you should focus on understanding the principles of oscillatory motion, including the mathematical description of SHM, the role of restoring forces, and the calculation of oscillation periods. You should learn how energy is conserved and transferred between kinetic and potential forms in these systems. Additionally, grasp how different parameters like mass, spring constant, and pendulum length influence the motion, and be able to solve related problems using these concepts.

Simple Harmonic Motion (SHM)

Simple Harmonic Motion (SHM) is the repetitive back-and-forth motion of an object where the restoring force is directly proportional to its displacement from a fixed point (usually the equilibrium position) and directed toward that point.

Key Characteristics of SHM

Restoring Force (F): F=−kx
- Where k is the spring constant (N/m) and x is the displacement from equilibrium (m).
- The negative sign indicates that the force is opposite to the displacement.
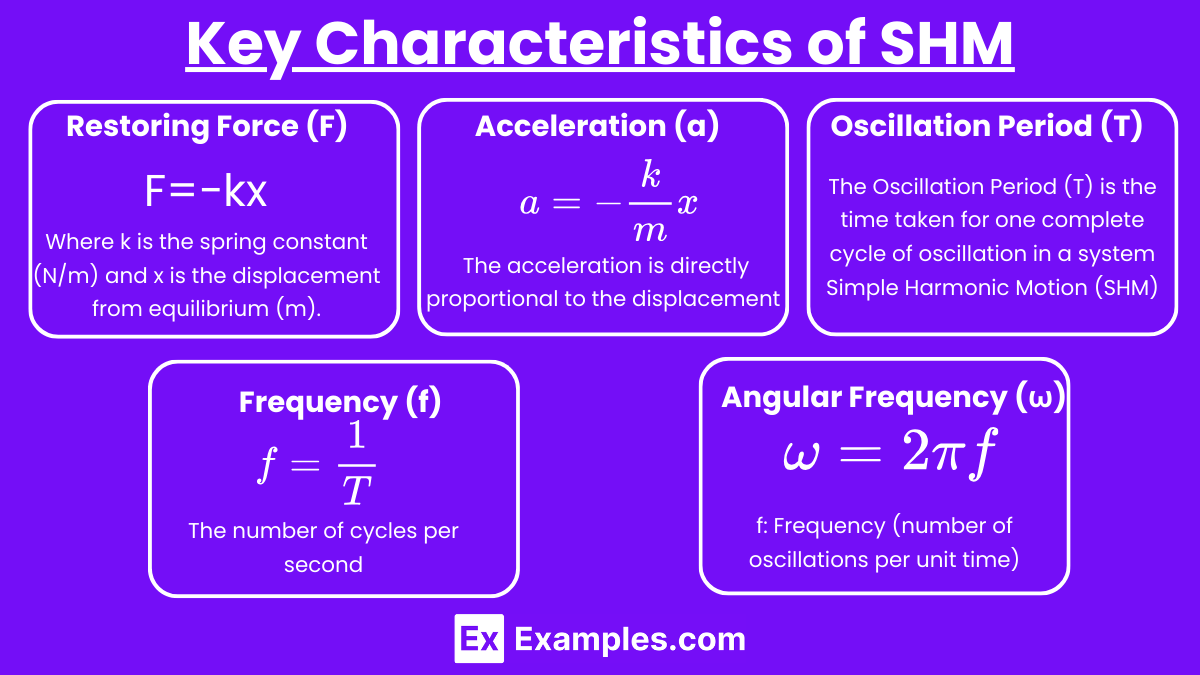
Acceleration (a):
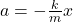
- m is the mass of the object.
- The acceleration is directly proportional to the displacement but in the opposite direction.
Oscillation Period (T): The Oscillation Period (T) is the time taken for one complete cycle of oscillation in a system undergoing Simple Harmonic Motion (SHM). The formula for the period T depends on the type of system:
Frequency (f): The number of cycles per second, $f = \frac{1}{T}$ .
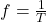Angular Frequency (ω): $\omega = 2\pi f \quad \text{or} \quad \omega = \sqrt{\frac{k}{m}}$ .

Equations of Motion for SHM

Displacement as a function of time:
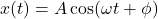
- A is the amplitude (maximum displacement).
- ϕ is the phase constant, determined by initial conditions.
Velocity as a function of time: $v(t) = -A\omega \sin(\omega t + \phi)$
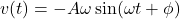
Acceleration as a function of time: $a(t) = -A\omega^2 \cos(\omega t + \phi)$

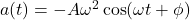
Energy in SHM

Total Mechanical Energy (E): Constant for SHM, .
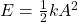- Kinetic Energy (KE): $KE = \frac{1}{2} mv^{2} = \frac{1}{2} k ( A^{2} - x^{2} )$
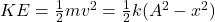
- Potential Energy (PE): $PE = \frac{1}{2} k x^{2}$
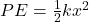
- Energy oscillates between kinetic and potential forms, but the total remains constant.

Springs and Hooke’s Law

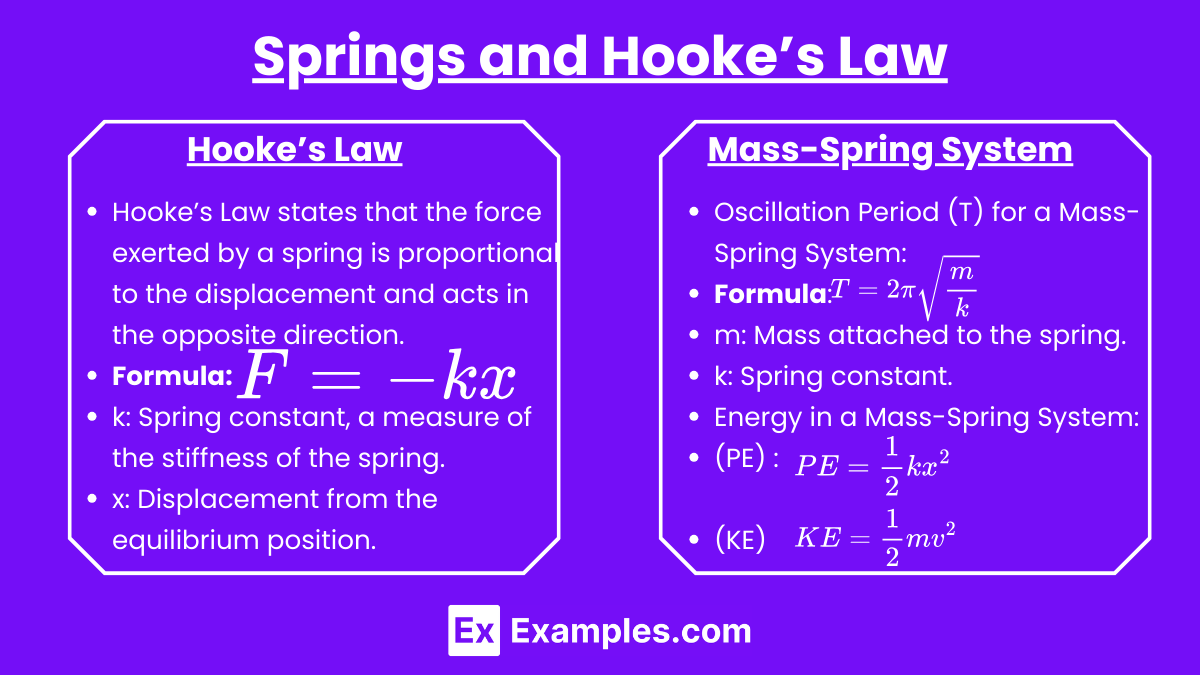
Hooke’s Law

Hooke’s Law states that the force exerted by a spring is proportional to the displacement and acts in the opposite direction:
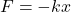
- k: Spring constant, a measure of the stiffness of the spring.
- x: Displacement from the equilibrium position.

Mass-Spring System

Oscillation Period (T) for a Mass-Spring System:
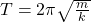
- m: Mass attached to the spring.
- k: Spring constant.
Frequency (f): $f = \frac{1}{T} = \frac{1}{2\pi} \sqrt{\frac{k}{m}}$ .
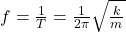Energy in a Mass-Spring System:
- Potential Energy (PE):
  $PE = \frac{1}{2} k x^{2}$
- Kinetic Energy (KE):
  $KE = \frac{1}{2} mv^{2}$

Damped and Driven Harmonic Oscillators

Damping: The gradual loss of amplitude due to resistive forces like friction.
Driven Oscillators: When an external force drives the system, it can lead to resonance if the driving frequency matches the natural frequency.

Pendulums

A pendulum is a weight suspended from a fixed point so that it can swing freely back and forth under the influence of gravity. The motion of a pendulum can be periodic, meaning it repeats itself at regular intervals.

Simple Pendulum

A mass (called the bob) attached to a string or rod of fixed length, swinging back and forth under the influence of gravity.
Restoring Force: F=−mgsin⁡(θ), where θ is the angular displacement.
For small angles (θ in radians): $F \approx -mg\theta$ and the motion approximates SHM.

Period of a Simple Pendulum

Oscillation Period (T):
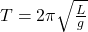
- L: Length of the pendulum.
- g: Acceleration due to gravity (9.8 m/s29.8 \, m/s^29.8m/s2).

Energy in a Simple Pendulum

Total Mechanical Energy (E): Remains constant if we neglect air resistance and friction.
- Potential Energy (PE): PE = mgh, where h = L(1−cos⁡θ).
- Kinetic Energy (KE): KE = 1/2mv², where vvv is the speed of the bob.

Physical Pendulum

A more generalized pendulum where the mass is distributed along its length (e.g., a swinging rod).
Oscillation Period (T):
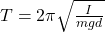
- I: Moment of inertia about the pivot point.
- d: Distance from the pivot to the center of mass.

Examples

Example 1: Mass-Spring System

Consider a mass attached to a horizontal spring on a frictionless surface. When the mass is pulled and then released, it oscillates back and forth around the equilibrium position. The restoring force from the spring follows Hooke’s Law, causing the mass to exhibit simple harmonic motion. The system’s motion depends on the spring constant and the mass.

Example 2: Pendulum in a Clock

The swinging pendulum in a traditional grandfather clock is a classic example of SHM. As the pendulum swings back and forth, gravity acts as the restoring force, pulling it back towards its lowest point. The period of the pendulum’s motion is primarily determined by its length and the acceleration due to gravity.

Example 3: Vertical Mass-Spring System

Imagine a spring hanging vertically with a mass attached to its end. When the mass is pulled downward and released, it oscillates up and down. The interplay between the spring’s restoring force and gravity creates simple harmonic motion. The period of this motion depends on both the mass and the spring constant.

Example 4: Torsional Pendulum

A torsional pendulum consists of a disk or bar that twists around its central axis due to a restoring torque. When the object is twisted and released, it oscillates back and forth in SHM. The period of this motion is influenced by the torsional stiffness of the wire or rod and the moment of inertia of the object.

Example 5: Bungee Jumping Cord

When a person jumps off a bridge with a bungee cord, the motion that follows is a form of SHM. The bungee cord acts like a spring, stretching as the person falls and then pulling them back up. The person oscillates up and down, experiencing simple harmonic motion due to the elastic properties of the cord. The characteristics of this motion are determined by the cord’s elasticity and the mass of the person.

Multiple Choice Questions

Question 1

Which of the following best describes the motion of a mass attached to a spring when it is displaced and released?

A) The mass moves in a straight line and then stops.
B) The mass moves in a circular path.
C) The mass oscillates back and forth around its starting position.
D) The mass moves randomly.

Answer: C) The mass oscillates back and forth around its starting position.

Explanation: When a mass attached to a spring is displaced and released, it undergoes simple harmonic motion, which means it moves back and forth around its equilibrium (starting) position.

Question 2

For a simple pendulum, which factor primarily affects the time it takes to complete one swing (its period)?

A) The weight of the pendulum.
B) The length of the string.
C) The color of the pendulum.
D) The angle it is released from.

Answer: B) The length of the string.

Explanation: The period of a simple pendulum mainly depends on the length of the string. A longer string means a longer period (more time to complete one swing), and a shorter string means a shorter period.

Question 3

If the amplitude (the maximum distance from the center) of a mass-spring system is increased, what happens to the time it takes for one complete oscillation (the period)?

A) The period stays the same.
B) The period increases.
C) The period decreases.
D) The period stops.

Answer: A) The period stays the same.

Explanation: In a mass-spring system, the period of oscillation does not depend on the amplitude. Whether the mass moves a little or a lot, the time to complete one cycle remains the same.