Torque and Rotational Statics

Torque and Rotational Statics are fundamental concepts in rotational mechanics, essential for mastering AP Physics. Torque refers to the rotational equivalent of force, causing objects to rotate about an axis. Understanding how forces create rotational motion and maintain equilibrium is crucial for solving problems involving objects in rotational balance. In AP Physics, these principles help analyze real-world scenarios, from balancing beams to calculating rotational forces in various systems, laying the foundation for more advanced topics in rotational dynamics.

Learning Objectives

By studying Torque and Rotational Statics for the AP Physics exam, you should learn how to calculate torque and understand its relation to force and lever arm. You should master the conditions for rotational equilibrium, ensuring that the sum of forces and torques equals zero. Additionally, understand the concept of moment of inertia and its impact on rotational motion, and be able to apply the parallel axis theorem. Finally, practice solving problems involving real-world applications of torque and rotational statics.

1. Introduction to Torque

Torque is a measure of the rotational force applied to an object. It causes an object to rotate about an axis or pivot point. The concept of torque is similar to force in linear motion, but instead of causing linear acceleration, torque causes angular acceleration.

Formula for Torque:

\( \text{Torque}(\tau) = \text{Force}(F) \times \text{Lever Arm}(r) \times \sin(\theta) \)

• τ: Torque (measured in Newton-meters, Nm)
• F: Force applied (measured in Newtons, N)
• r: Lever arm or distance from the axis of rotation to the point where the force is applied (measured in meters, m)
• θ: Angle between the force vector and the lever arm

Key Points:

• Torque is a vector quantity, meaning it has both magnitude and direction.
• The direction of torque is determined by the right-hand rule: curl your fingers in the direction of rotation caused by the force, and your thumb points in the direction of the torque vector.

2. Lever Arm and its Significance

The lever arm (also called the moment arm) is the perpendicular distance from the axis of rotation to the line of action of the force. The longer the lever arm, the greater the torque for the same applied force.

Example:

• Wrench Example: When you apply force to a wrench to turn a bolt, the distance from where you apply the force to the bolt’s center is the lever arm. Using a longer wrench increases the lever arm, thereby increasing the torque and making it easier to turn the bolt.

3. Conditions for Rotational Equilibrium (Rotational Statics)

Rotational equilibrium occurs when the net torque acting on a body is zero, resulting in no angular acceleration and maintaining constant rotational motion. An object is in rotational equilibrium when the sum of all torques acting on it is zero. This means that the object will not have any angular acceleration and will either remain at rest or continue rotating at a constant angular velocity.

Conditions for Equilibrium:

1. Translational Equilibrium: The sum of all forces acting on the object must be zero. This ensures no linear acceleration. \( \sum F = 0 \)
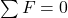
2. Rotational Equilibrium: The sum of all torques about any axis must be zero. This ensures no angular acceleration. \( \sum \tau = 0 \)
   

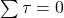
4. Analyzing Torque in Rotational Statics

When solving problems involving rotational statics, follow these steps:

1. Identify the pivot point (axis of rotation). This is the point about which you will calculate the torques. You can choose any point, but selecting a point where forces cancel out can simplify the calculation.
2. Determine all forces acting on the object and their points of application.
3. Calculate the torque produced by each force. Remember, only the component of the force perpendicular to the lever arm contributes to the torque.
4. Set the sum of all torques equal to zero and solve for the unknowns.

5. Common Scenarios Involving Torque

• Seesaw (Teeter-Totter): Consider two masses at different distances from the pivot. To balance the seesaw, the torque produced by each mass around the pivot must be equal and opposite.
• Beam with Supports: A horizontal beam supported at two points can have various forces acting on it (e.g., its weight and additional loads). You need to calculate the torques around one support to find the reaction forces at the supports.
• Ladder Against a Wall: For a ladder leaning against a frictionless wall, analyze the torques about the point where the ladder touches the ground to ensure rotational equilibrium.

6. Moment of Inertia and Its Role in Rotation

The moment of inertia (I) is a measure of an object’s resistance to changes in its rotation and is analogous to mass in linear motion. The larger the moment of inertia, the more torque is required to achieve a given angular acceleration.

Formula for Moment of Inertia:

\( I = \sum m_i r_i^2 \)

• m_i​: Mass of the i-th particle
• r_i​: Distance of the i-th particle from the axis of rotation

Different shapes have different moments of inertia, which depend on their mass distribution relative to the axis of rotation.

Common Moments of Inertia:

• Solid Cylinder/Disc (about its central axis): 1​ / 2 MR²
• Solid Sphere (about its central axis): 2 / 5 MR²
• Thin Rod (about its end): 1 / 3 ML²
• Hollow Cylinder/Disc (about its central axis): MR²

7. The Parallel Axis Theorem

The Parallel Axis Theorem allows you to find the moment of inertia of an object about any axis, given its moment of inertia about a parallel axis through its center of mass.

Formula:

\( I = I_{cm} + M d^2 \)

• Icm​: Moment of inertia about the center of mass
• M: Mass of the object
• d: Distance between the center of mass and the new axis

8. Angular Momentum and Conservation

Angular Momentum (L) is a vector quantity representing the product of an object’s rotational inertia and its angular velocity.

Formula:

\( L = I \omega \)

• I: Moment of inertia
• ω: Angular velocity

Conservation of Angular Momentum states that if no external torque acts on a system, the total angular momentum remains constant.

Examples

Example 1: Seesaw Balance

A classic example of torque in action is a seesaw. When two children of different weights sit on opposite ends, the seesaw will only balance when the torque produced by each child is equal. The child with greater weight needs to sit closer to the fulcrum (the pivot point) to balance the lighter child sitting farther away. This demonstrates how torque depends on both the force applied (the child’s weight) and the distance from the pivot.

Example 2: Opening a Door

When you push a door open, the force you apply creates torque about the door’s hinges. The farther from the hinges you push, the easier it is to open the door. This is because the torque increases with the distance from the pivot point. This principle is why door handles are typically placed far from the hinges—to maximize the torque for a given force and make the door easier to open.

Example 3: Wrenching a Bolt

Using a wrench to loosen a bolt involves torque. When you apply force to the end of the wrench, torque is generated around the bolt. The longer the wrench, the greater the torque for the same applied force, making it easier to turn the bolt. This example shows how tools are designed to increase torque, allowing us to apply larger forces with less effort.

Example 4: Balancing a Tightrope

A tightrope walker uses a long pole to help maintain balance while walking on the rope. The pole increases the moment of inertia, making it harder for the walker to rotate around the rope. This, combined with subtle shifts in the pole, helps the walker control the torque and maintain stability, preventing tipping over.

Example 5: Hanging a Picture Frame

When hanging a picture frame, it’s essential to place the hook or nail at the correct spot to ensure the frame remains level. The torque on either side of the frame’s pivot (the hook) must be balanced to keep the frame straight. If the torque is unbalanced, the frame will rotate until it reaches a new equilibrium, typically hanging crookedly.

Multiple Choice Questions

Question 1

Torque is the product of force and which of the following?

a) Mass
b) Velocity
c) Distance from the pivot
d) Acceleration

Correct Answer: c) Distance from the pivot

Explanation: Torque (τ) is calculated as the product of the force applied and the perpendicular distance from the pivot or axis of rotation to the point where the force is applied. Mathematically, τ=F×r, where r is the distance from the pivot.

Question 2

If a force is applied at the center of a rotating object, what is the torque generated?

a) Maximum
b) Zero
c) Depends on the mass of the object
d) Infinite

Correct Answer: b) Zero

Explanation: Torque is given by τ=F×r. If the force is applied at the center of rotation (where r=0), the distance r is zero, so the torque will be zero regardless of the force applied.

Question 3

Which of the following conditions must be true for an object to be in rotational equilibrium?

a) The object must be moving at a constant speed.
b) The net torque acting on the object must be zero.
c) The net force acting on the object must be zero.
d) The object must be at rest.

Correct Answer: b) The net torque acting on the object must be zero

Explanation: Rotational equilibrium occurs when the sum of all torques acting on an object is zero. This means there is no net rotational effect, and the object either remains at rest or continues rotating at a constant angular velocity.