Describing End Behavior of Polynomial and Rational Functions

In AP Precalculus, understanding the end behavior of polynomial and rational functions is crucial for analyzing how these functions behave as the input values approach infinity or negative infinity. The end behavior of a polynomial function is determined by its degree and leading coefficient, influencing whether the graph rises or falls. For rational functions, the degrees of the numerator and denominator dictate horizontal asymptotes or unbounded behavior. Mastering these concepts aids in predicting long-term function behavior, an essential skill for success in calculus and beyond.

Learning Objectives

n studying the end behavior of polynomial and rational functions for AP Precalculus, you should learn how to analyze the degree and leading coefficient of a polynomial to predict the behavior as x→∞ and x→−∞. Additionally, you should understand how the degrees of the numerator and denominator in a rational function determine horizontal asymptotes or unbounded behavior. Mastering these concepts will enable you to effectively describe and graph the long-term behavior of functions in various mathematical contexts.

End Behavior of Polynomial Functions

The end behavior of a polynomial function describes how the function behaves as x approaches ∞ (positive infinity) and −∞ (negative infinity). It is primarily determined by the degree and the leading coefficient of the polynomial.

• Degree of the Polynomial:
  • If the degree is even, the ends of the graph go in the same direction. Both ends either rise or fall.
  • If the degree is odd, the ends of the graph go in opposite directions. One end rises and the other falls.
• Leading Coefficient:
  • If the leading coefficient is positive:
    • For even-degree polynomials: the graph rises to +∞ as x→∞ and rises to +∞ as x→−∞.
    • For odd-degree polynomials: the graph rises to +∞ as x→∞ and falls to −∞ as x→−∞.
  • If the leading coefficient is negative:
    • For even-degree polynomials: the graph falls to −∞ as x→∞ and falls to −∞ as x→−∞.
    • For odd-degree polynomials: the graph falls to −∞ as x→∞ and rises to +∞ as x→−∞.

End Behavior of Rational Functions

For rational functions, which are of the form ​, where both p(x) and q(x) are polynomials, the end behavior is determined by the degrees of the numerator and denominator.

Degree of the Numerator vs. Degree of the Denominator:

• Degree of numerator = Degree of denominator:
• The end behavior approaches the horizontal asymptote at \(\frac{\text{leading coefficient of numerator}}{\text{leading coefficient of denominator}} \)
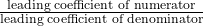
• Degree of numerator < Degree of denominator:
• The end behavior approaches the horizontal asymptote at y = 0.
• Degree of numerator > Degree of denominator:
• There is no horizontal asymptote. The end behavior will approach either ∞ or −∞, depending on the signs of the leading coefficients.

Summary of End Behavior

Polynomial Functions : The end behavior of polynomial functions is influenced by the degree of the polynomial and the sign of the leading coefficient. If the degree is even, both ends of the graph will move in the same direction—either both up or both down. For an odd-degree polynomial, the ends of the graph will move in opposite directions, with one end rising and the other falling. Additionally, the sign of the leading coefficient plays a crucial role: a positive leading coefficient causes the graph to rise towards infinity as x approaches both positive and negative infinity (for even degrees) or rise to infinity in one direction and fall in the other (for odd degrees).

Rational Functions : For rational functions, the end behavior is determined by comparing the degree of the numerator to the degree of the denominator. If the degrees are equal, the function approaches a horizontal asymptote, which can be found by dividing the leading coefficients of the numerator and denominator. If the degree of the numerator is less than the degree of the denominator, the function approaches a horizontal asymptote at y = 0, meaning the graph flattens as x approaches infinity. However, if the degree of the numerator is greater than the degree of the denominator, the function has no horizontal asymptote, and its end behavior tends towards infinity or negative infinity, reflecting unbounded growth or decay.

Examples

Example 1: Polynomial Function 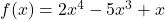\( f(x) = 2x^4 – 5x^3 + x \)

Since the highest degree term is 2x⁴ and the degree is even, the end behavior is the same in both directions. The leading coefficient is positive, so as x→∞, f(x)→∞, and as x→−∞, f(x)→∞. Therefore, both ends of the graph rise toward infinity.

Example 2: Polynomial Function 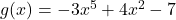\( g(x) = -3x^5 + 4x^2 – 7 \)

Here, the degree is 5, which is odd, and the leading coefficient is negative. Since the degree is odd, the ends of the graph go in opposite directions. As x→∞, g(x)→−∞, and as x→−∞, g(x)→∞. The graph falls on the right and rises on the left.

Example 3: Rational Function 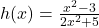\( h(x) = \frac{x^2 – 3}{2x^2 + 5} \)

The degrees of the numerator and denominator are both 2, so the end behavior approaches the horizontal asymptote. The leading coefficients of the numerator and denominator are 1 and 2, respectively. Therefore, as x→∞ or x→−∞, \( h(x) \to \frac{1}{2} \)​. The graph flattens out at \( y = \frac{1}{2} \)​.

Example 4: Rational Function 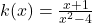\( k(x) = \frac{x + 1}{x^2 – 4} \)

In this case, the degree of the numerator is 1, and the degree of the denominator is 2. Since the degree of the denominator is greater than that of the numerator, the end behavior approaches the horizontal asymptote y = 0. As x→∞ or x→−∞, k(x)→0.

Example 5: Rational Function 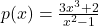\( p(x) = \frac{3x^3 + 2}{x^2 – 1} \)

The degree of the numerator is 3, and the degree of the denominator is 2. Since the degree of the numerator is greater, there is no horizontal asymptote, and the function has unbounded end behavior. As x→∞, p(x)→∞, and as x→−∞, p(x)→−∞. The graph rises on the right and falls on the left.

Multiple Choice Questions

Question 1

What is the end behavior of the polynomial function f(x)=−2x⁶+3x²−5?

A) As x→∞, f(x)→∞; as x→−∞, f(x)→∞
B) As x→∞, f(x)→∞; as x→−∞, f(x)→−∞
C) As x→∞, f(x)→−∞; as x→−∞, f(x)→−∞
D) As x→∞, f(x)→−∞; as x→−∞, f(x)→∞

Correct Answer: C) As x→∞, f(x)→−∞; as x→−∞, f(x)→−∞

Explanation: The polynomial f(x)=−2x⁶+3x²−5 has an even degree (6) and a negative leading coefficient (-2). For polynomials with an even degree, the end behavior will be the same in both directions. Since the leading coefficient is negative, both ends of the graph will go to negative infinity.

Question 2

Which of the following is the horizontal asymptote of the rational function \( g(x) = \frac{3x^2 + 4}{5x^2 – 7} \) ?

A) y = 0
B) \( y = \frac{3}{5} \)
C) y = 5
D) y = 3

Correct Answer: B) \( y = \frac{3}{5} \)

Explanation: For the rational function \( g(x) = \frac{3x^2 + 4}{5x^2 – 7} \)​​, the degree of the numerator and the degree of the denominator are both 2. When the degrees of the numerator and denominator are equal, the horizontal asymptote is found by dividing the leading coefficients of the numerator and denominator. In this case, the leading coefficient of the numerator is 3, and the leading coefficient of the denominator is 5, so the horizontal asymptote is \( y = \frac{3}{5} \)​.

Question 3

What is the end behavior of the rational function \( h(x) = \frac{2x + 1}{x^2 + 3x + 2} \)​?

A) As x→∞, h(x)→2; as x→−∞, h(x)→2
B) As x→∞, h(x)→0; as x→−∞, h(x)→0
C) As x→∞, h(x)→∞; as x→−∞, h(x)→∞
D) As x→∞, h(x)→−∞; as x→−∞, h(x)→−∞

Correct Answer: B) As x→∞, h(x)→0; as x→−∞, h(x)→0

Explanation: In the rational function \( h(x) = \frac{2x + 1}{x^2 + 3x + 2} \)​, the degree of the denominator (2) is greater than the degree of the numerator (1). When the degree of the denominator is greater than the degree of the numerator, the end behavior of the function approaches a horizontal asymptote of y = 0. Thus, as x→∞ or x→−∞, the function approaches 0.