Describing the Impact of a Transformation Matrix on a Graphical Object

Last Updated: September 23, 2024

Notes

In AP Precalculus, transformation matrices play a key role in altering the position, size, and orientation of graphical objects in the coordinate plane. By applying various matrices, you can perform transformations like translation, scaling, rotation, reflection, and shearing. Each type of transformation is represented by a unique matrix that manipulates the object’s points to produce the desired effect. Understanding the impact of these matrices is essential for interpreting how graphical objects change, enhancing problem-solving skills, and preparing for advanced mathematical concepts.

Free AP Precalculus Practice Test

Learning Objectives

For the topic “Describing the Impact of a Transformation Matrix on a Graphical Object” in AP Precalculus, you should learn how to apply transformation matrices to modify graphical objects. This includes understanding translation, scaling, rotation, reflection, and shearing matrices. You should be able to describe how each transformation affects the object’s position, size, orientation, or shape. Additionally, you need to perform matrix multiplication to implement transformations and analyze how composite transformations combine multiple effects on an object in a coordinate plane.

Describing the Impact of a Transformation Matrix on a Graphical Object

In AP Precalculus, transformation matrices are used to alter the position, size, and orientation of graphical objects in a coordinate plane. A transformation matrix applies linear transformations, such as translation, scaling, reflection, rotation, and shearing, to a vector representing a point or object.

Translation

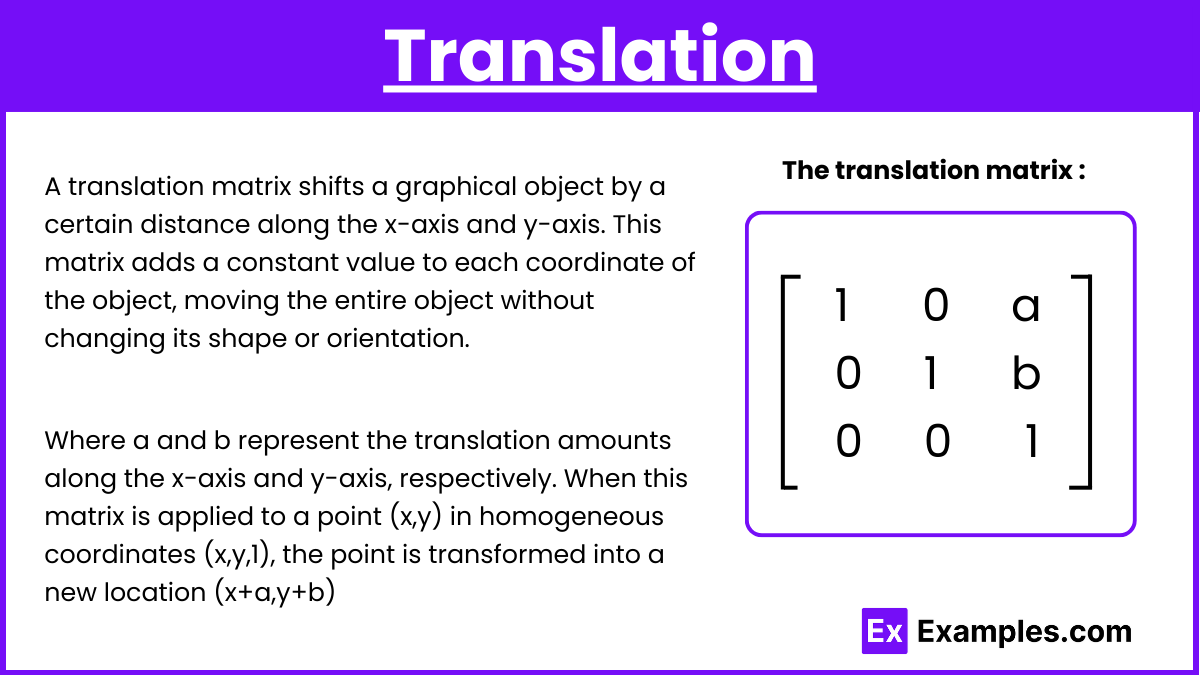
A translation matrix shifts a graphical object by a certain distance along the x-axis and y-axis. This matrix adds a constant value to each coordinate of the object, moving the entire object without changing its shape or orientation.

The translation matrix is represented as:

$\begin{bmatrix} 1 & 0 & a \\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix}$

Where a and b represent the translation amounts along the x-axis and y-axis, respectively. When this matrix is applied to a point (x,y) in homogeneous coordinates (x,y,1), the point is transformed into a new location (x+a,y+b), effectively moving the point by a units in the x-direction and b units in the y-direction.

Scaling

A scaling matrix changes the size of an object by stretching or compressing it along the x and y directions. The scaling factors determine how much the object is enlarged or reduced. A scaling factor greater than 1 enlarges the object, while a factor between 0 and 1 shrinks it.

The scaling matrix is represented as:

$\begin{bmatrix} S_x & 0 \\ 0 & S_y \end{bmatrix}$

When the scaling matrix is applied to a point (x,y), the new coordinates of the scaled point become (x′ = Sx⋅x, y′ = Sy⋅y). This transformation alters the size of the object without changing its shape, provided the scaling factors in both directions are equal. If Sx and Sy differ, the object will be stretched or compressed asymmetrically, resulting in a change in aspect ratio.

Rotation

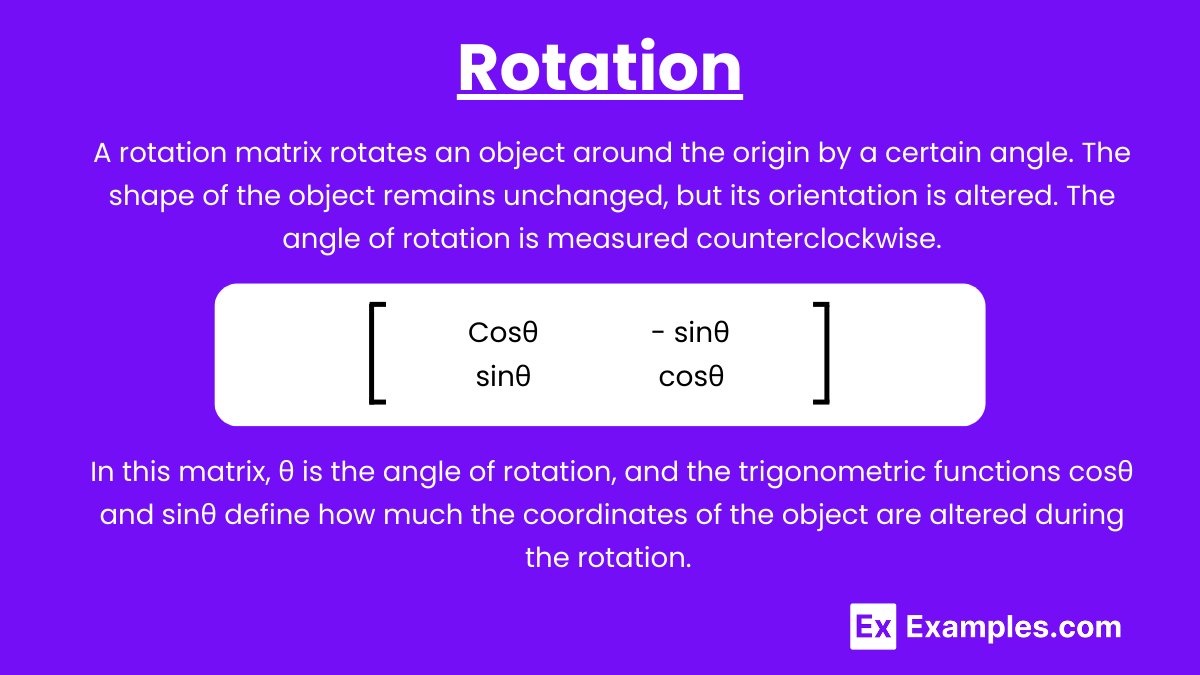
A rotation matrix rotates an object around the origin by a certain angle. The shape of the object remains unchanged, but its orientation is altered. The angle of rotation is measured counterclockwise.

The rotation matrix for a counterclockwise rotation by an angle θ is:

$\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$

In this matrix, θ is the angle of rotation, and the trigonometric functions cos⁡θ and sin⁡θ define how much the coordinates of the object are altered during the rotation. The cosine of the angle determines the projection of the point onto the x-axis, while the sine of the angle determines the projection onto the y-axis.

Reflection

A reflection matrix flips an object across a specific axis. Common reflections include reflecting across the x-axis, y-axis, or origin. Each reflection produces a mirror image of the object with respect to the chosen axis.

Reflection across the x-axis:

$\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$

Reflection across the y-axis:

$\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}$

Shearing

Shearing distorts the shape of an object by slanting it in one direction, either horizontally or vertically. This transformation preserves the area but alters the angles between lines in the object.

The shearing matrix for horizontal and vertical shear is:

$\begin{bmatrix} 1 & k_x \\ k_y & 1 \end{bmatrix}$

Where kx and ky are the shear factors in the x and y directions.

Examples

Example 1. Translation

Imagine a triangle with vertices at coordinates (2, 1), (4, 1), and (3, 3). Applying a translation matrix with a shift of 3 units along the x-axis and 2 units along the y-axis will move the entire triangle. The new coordinates of the triangle’s vertices would be (5, 3), (7, 3), and (6, 5). The object retains its shape and size, but its position in the plane has changed.

Example 2. Scaling

Consider a rectangle with coordinates (1, 2), (3, 2), (1, 4), and (3, 4). By applying a scaling matrix with factors of 2 in both x and y directions, the rectangle doubles in size. The new coordinates of the rectangle would be (2, 4), (6, 4), (2, 8), and (6, 8). The object becomes larger, maintaining the same proportions but increasing its area.

Example 3. Rotation

Take a square with coordinates (0, 0), (2, 0), (2, 2), and (0, 2). Applying a 90-degree counterclockwise rotation matrix will rotate the square about the origin. The new coordinates of the square will be (0, 0), (0, 2), (-2, 2), and (-2, 0). The square’s orientation changes, but its shape and size remain the same.

Example 4. Reflection

Assume a pentagon with vertices at (1, 2), (3, 2), (4, 3), (2, 4), and (0, 3). Reflecting the pentagon across the x-axis using a reflection matrix will flip the pentagon upside down. The new vertices of the pentagon would be (1, -2), (3, -2), (4, -3), (2, -4), and (0, -3). The reflection creates a mirror image of the original shape across the x-axis.

Example 5. Shearing

Imagine a parallelogram with coordinates (1, 1), (3, 1), (2, 3), and (4, 3). Applying a horizontal shearing matrix with a factor of 1.5 will slant the object to the right, distorting its shape. The new coordinates of the parallelogram would be (1, 1), (4.5, 1), (2, 3), and (5.5, 3). The parallelogram’s shape changes, as it becomes skewed along the x-axis, but its area remains unchanged.

Multiple Choice Questions

Question 1

Which transformation matrix represents a counterclockwise rotation by 90 degrees around the origin?

A. $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$
B. $\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$
C. $\begin{bmatrix} \cos(90^\circ) & -\sin(90^\circ) \\ \sin(90^\circ) & \cos(90^\circ) \end{bmatrix}$
D. $\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$

Answer: B

Explanation: When rotating an object by 90 degrees counterclockwise, the rotation matrix takes the form:

Since cos(90∘) = 0 and sin(90∘) = 1, the rotation matrix becomes:

$\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$

Thus, option B is correct.

Question 2

What effect does the following matrix have on an object?

$\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}$

A. The object is rotated by 180 degrees.
B. The object is reflected across the y-axis.
C. The object is scaled by a factor of 2.
D. The object is translated by 2 units in the x and y directions.

Answer: C

Explanation: This matrix represents a scaling transformation. The values 2 and 2 on the diagonal indicate that the object is scaled equally in both the x and y directions by a factor of 2. This means the object is enlarged, maintaining its proportions, and each point on the object moves twice as far from the origin. Hence, the correct answer is C.

Question 3

Which transformation is represented by the matrix:

$\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$

A. Reflection across the x-axis
B. Reflection across the y-axis
C. Rotation by 180 degrees
D. Shear transformation

Answer: A

Explanation: The matrix $\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$ reflects points across the x-axis. This is because the y-coordinates of points are negated, while the x-coordinates remain the same. As a result, the object is flipped vertically, creating a mirror image across the x-axis. Therefore, option A is correct.