Relating Right Triangle Trigonometry to the Sine, Cosine, and Tangent Functions
In AP Precalculus, right triangle trigonometry forms the foundation for understanding sine, cosine, and tangent functions. These functions are defined based on the ratios of the sides of a right triangle. The sine function relates the ratio of the length of the opposite side to the hypotenuse, cosine relates the adjacent side to the hypotenuse, and tangent connects the opposite side to the adjacent side. Mastery of these functions is crucial for solving various trigonometric problems and analyzing periodic phenomena.
Learning Objectives
For the topic “Relating Right Triangle Trigonometry to the Sine, Cosine, and Tangent Functions” in AP Precalculus, you should focus on understanding how the trigonometric ratios of sine, cosine, and tangent are defined using the sides of a right triangle. Learn to apply these ratios to solve for unknown side lengths and angles in right triangles, and explore how these functions relate to the unit circle. Be able to use these functions in real-world applications and problem-solving scenarios involving right triangles.
Right Triangle Trigonometry
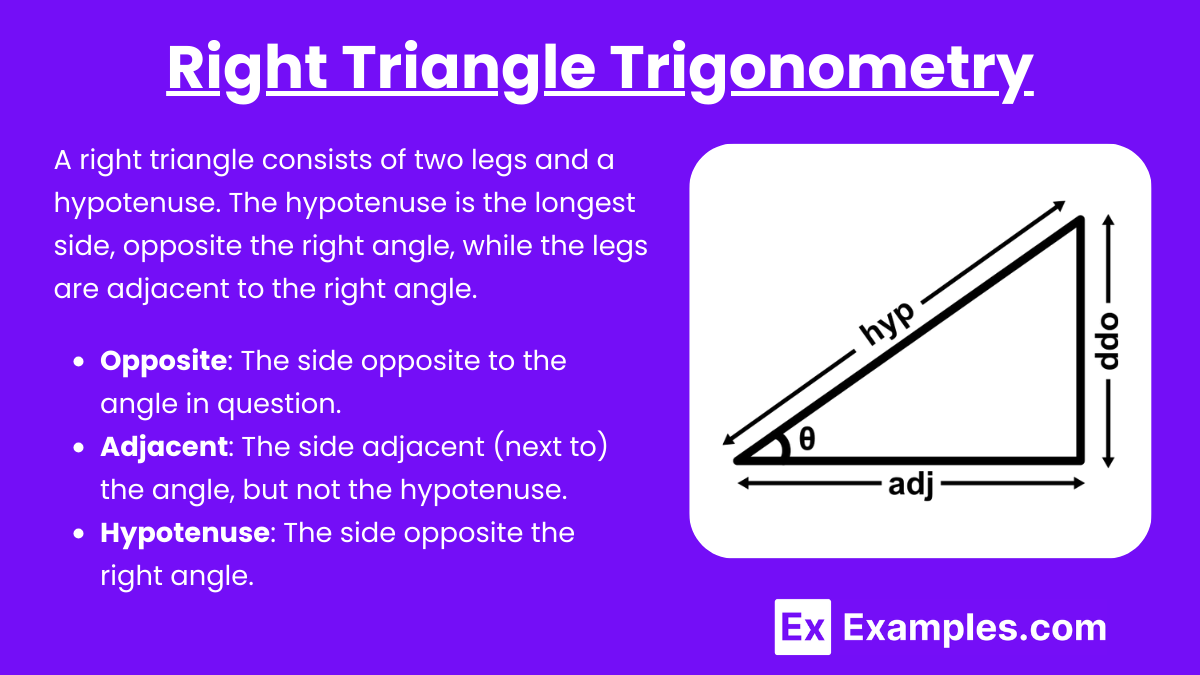
A right triangle consists of two legs and a hypotenuse. The hypotenuse is the longest side, opposite the right angle, while the legs are adjacent to the right angle.
- Opposite: The side opposite to the angle in question.
- Adjacent: The side adjacent (next to) the angle, but not the hypotenuse.
- Hypotenuse: The side opposite the right angle.
Trigonometric Ratios
In a right triangle, the trigonometric functions sine, cosine, and tangent are defined as ratios of the sides of the triangle with respect to a given angle, typically denoted as θ.
Sine Function (sin θ)
The sine of an angle (θ) is the ratio of the length of the opposite side to the length of the hypotenuse.
\(\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}} \)
In a right triangle, sinθ (sine of angle θ) is the ratio of the length of the side opposite the angle θ to the length of the hypotenuse.
Example: In a right triangle with an angle θ\thetaθ, if the side opposite to θ is 3 and the hypotenuse is 5, then: \(\sin \theta = \frac{3}{5} \)
Cosine Function (cos θ)
The cosine of an angle (θ) is the ratio of the length of the adjacent side to the length of the hypotenuse.
\(\cos \theta = \frac{\text{Adjacent}}{\text{Hypotenuse}} \)
In a right triangle, cosθ (cosine of angle θ) is the ratio of the length of the side adjacent to the angle θ to the length of the hypotenuse.
Example: In a triangle where the adjacent side to angle θ is 4 and the hypotenuse is 5, then: \(\cos \theta = \frac{4}{5} \)
.
Tangent Function (tan θ)
The tangent of an angle (θ) is the ratio of the length of the opposite side to the length of the adjacent side.
\(\tan \theta = \frac{\text{Opposite}}{\text{Adjacent}} \)
In a right triangle, tanθ (tangent of angle θ) is the ratio of the length of the side opposite the angle θ to the length of the side adjacent to the angle θ.
Example: In a triangle where the opposite side to θ is 3 and the adjacent side is 4, then: \(\tan \theta = \frac{3}{4} \)
Applications of Right Triangle Trigonometry
- Solving for Missing Angles and Sides: Trigonometric functions can help determine unknown side lengths or angles in right triangles when partial information is known. This is useful in fields like architecture, where calculating angles and dimensions is essential.
- Engineering and Architecture: In construction, sine, cosine, and tangent help determine structural angles, roof slopes, and forces acting on materials. Example: Engineers use trigonometry to calculate forces and stress in structures like bridges and buildings to ensure stability.
- Physics: Trigonometry is applied to model wave behavior (e.g., sound waves, light waves) and to resolve vector forces. Example: In projectile motion, trigonometric functions describe the trajectory of an object, where the horizontal and vertical components of motion depend on the sine and cosine of the angle of launch.
- Astronomy: Trigonometric functions help in calculating distances between celestial bodies and determining their movement. Example: The tangent function can be used to calculate the height of a star or satellite above the horizon by measuring its angle of elevation.
- Surveying: Surveyors use right triangle trigonometry to measure land. With basic tools like a theodolite, they can determine distances and angles to create maps or plots of land. Example: Using the tangent function, a surveyor can calculate the distance from the base of a building to its top by knowing the angle of elevation and height.
- Sound and Light Waves: Sine and cosine functions model periodic behavior like waves, which are essential in audio engineering, optics, and electromagnetism. Example: The amplitude and frequency of a sound wave can be described using trigonometric functions, helping sound engineers adjust sound quality.
Examples
Example 1: Finding the Height of a Building
Imagine you’re standing 50 meters away from a building and can measure the angle of elevation to the top of the building, which is 30°. To find the height of the building, you can use the tangent function, since you know the adjacent side (distance from the building) and need to find the opposite side (height). The equation is:
\(\tan(30^\circ) = \frac{\text{height}}{50} \)
You can then solve for the height using a calculator.
Example 2: Calculating the Length of a Ramp
A ramp needs to be installed with a 20° incline. If the vertical rise is 2 meters, you can find the length of the ramp using the sine function. The vertical rise represents the opposite side, and the hypotenuse is the length of the ramp. The equation is:
\(\sin(20^\circ) = \frac{2}{\text{ramp length}} \)
By solving, you’ll find the length of the ramp.
Example 3: Determining the Angle of a Roof
Suppose the slope of a roof is measured as 4 meters in height (opposite side) and 12 meters in length (adjacent side). To find the angle of elevation of the roof, you can use the tangent function. The equation is:
\(\tan(\theta) = \frac{4}{12} \)
By calculating the inverse tangent (arctan), you can determine the angle θ.
Example 4: Finding the Distance Across a River
If you’re standing on one side of a river and spot a tree on the opposite bank, you can measure the angle between your position, the base of the tree, and a point on your side of the river. If the angle is 45° and the distance from the point you’re standing to your observation point is 30 meters, you can use the sine function to find the width of the river (opposite side):
\(\sin(45^\circ) = \frac{\text{width}}{30} \)
This equation will give you the width of the river.
Example 5: Measuring the Angle Between Two Objects
You have two objects on the ground, one 5 meters to your left and another 10 meters straight in front. To determine the angle between them relative to your position, you can use the tangent function. Here, the distance to the first object (5 meters) is the opposite side, and the distance to the second (10 meters) is the adjacent side. The equation is:
\(\tan(\theta) = \frac{5}{10} \)
By solving for θ, you can find the angle between the two objects.
Multiple Choice Questions
Question 1
In a right triangle, if the angle θ is 30 degrees and the length of the hypotenuse is 10 units, what is the length of the side opposite θ?
A) 5 units
B) 10 units
C) 8.66 units
D) 3.5 units
Answer: A) 5 units
Explanation: For a right triangle with angle θ, the sine function relates the length of the side opposite θ to the hypotenuse. The sine of 30 degrees is sin(30∘)=0.5. Therefore, the length of the side opposite θ can be calculated as follows:
Opposite side = Hypotenuse × sin(θ) = 10 × 0.5 = 5 units
Question 2
In a right triangle, if the length of the adjacent side is 8 units and the length of the hypotenuse is 10 units, what is the cosine of the angle θ between the hypotenuse and the adjacent side?
A) 0.8
B) 0.6
C) 1
D) 0.5
Answer: A) 0.8
Explanation: The cosine function relates the length of the adjacent side to the hypotenuse. Specifically, \(\cos(\theta) = \frac{\text{Adjacent side}}{\text{Hypotenuse}}\). Given that the adjacent side is 8 units and the hypotenuse is 10 units, we have: \(\cos(\theta) = \frac{8}{10} = 0.8 \)
Question 3
If in a right triangle, the tangent of an angle θ is 1.5, what is the ratio of the length of the opposite side to the length of the adjacent side?
A) 1.5
B) 0.67
C) 0.5
D) 1
Answer: A) 1.5
Explanation: The tangent function relates the length of the opposite side to the length of the adjacent side. Specifically, \(\tan(\theta) = \frac{\text{Opposite side}}{\text{Adjacent side}}\). If tan(θ)=1.5, then the ratio of the length of the opposite side to the length of the adjacent side is 1.5