Calculating the Probability of a Random Event
In AP Statistics, calculating the probability of a random event is essential for understanding and predicting outcomes in various scenarios. Probability quantifies the likelihood of an event occurring, expressed as a number between 0 and 1. A probability of 0 means the event will not happen, while a probability of 1 indicates certainty. Using probability rules and models, students learn to analyze random phenomena and make informed decisions based on statistical data.
Learning Objectives
By studying AP Statistics, you will learn how to calculate the probability of a random event, enhancing your ability to predict and analyze outcomes in various contexts. You will understand the principles of probability, including the use of probability models and rules, and apply them to real-world situations. This knowledge will enable you to make data-driven decisions, interpret statistical information accurately, and gain a deeper comprehension of random phenomena and their implications.
Definition of Probability
Probability is a measure of the likelihood that an event will occur. It ranges from 0 to 1, where 0 indicates an impossible event, and 1 indicates a certain event.
Basic Probability Rules
- Complement Rule: The probability of an event not occurring is 1 minus the probability of it occurring.
\(P(A^c) = 1 – P(A)\) - Addition Rule for Mutually Exclusive Events: If two events cannot occur at the same time, the probability of either occurring is the sum of their individual probabilities.
\(P(A \cup B) = P(A) + P(B)\) - Addition Rule for Non-Mutually Exclusive Events: If two events can occur simultaneously, the probability of either occurring is the sum of their probabilities minus the probability of both occurring.
\(P(A \cup B) = P(A) + P(B) – P(A \cap B)\) - Multiplication Rule for Independent Events: If two events do not influence each other, the probability of both occurring is the product of their probabilities.
\(P(A \cap B) = P(A) \times P(B)\) - Multiplication Rule for Dependent Events: If two events are dependent, the probability of both occurring is the product of the probability of the first event and the probability of the second event given the first has occurred.
\(P(A \cap B) = P(A) \times P(B|A)\)
Types of Events
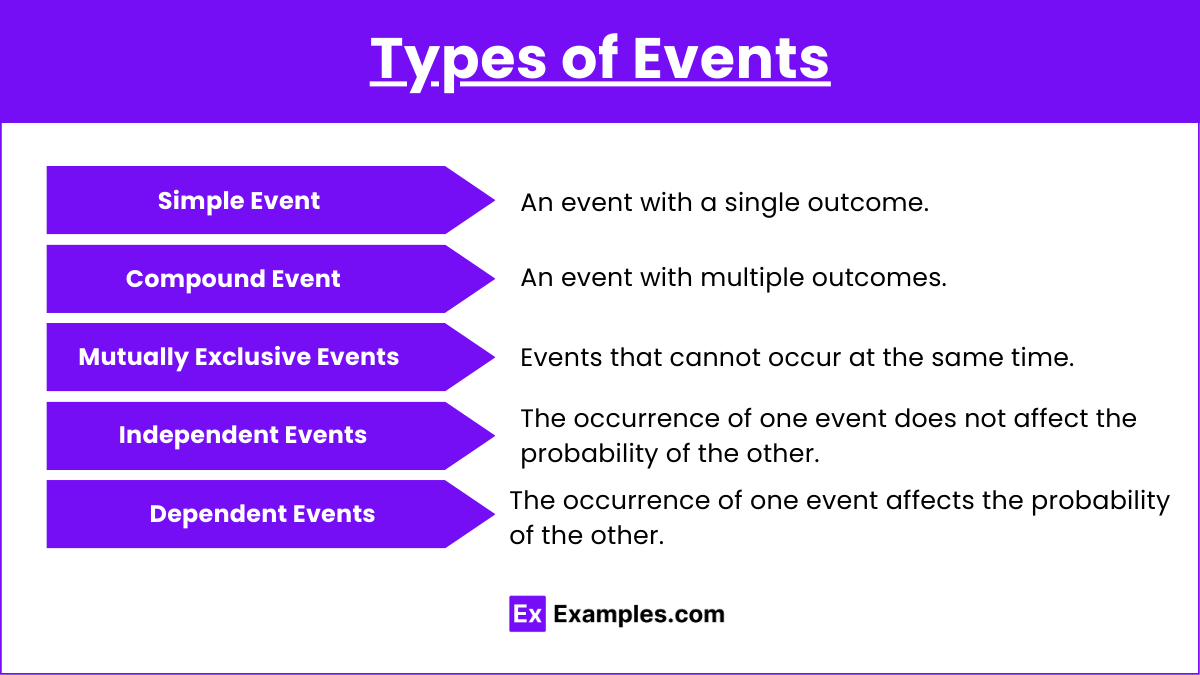
- Simple Event: An event with a single outcome.
- Compound Event: An event with multiple outcomes.
- Mutually Exclusive Events: Events that cannot occur at the same time.
- Independent Events: The occurrence of one event does not affect the probability of the other.
- Dependent Events: The occurrence of one event affects the probability of the other.
Conditional Probability
The probability of an event occurring given that another event has already occurred.
\(P(B|A) = \frac{P(A \cap B)}{P(A)}\)
Bayes’ Theorem
A way to find a conditional probability when the reverse conditional probability is known
\(P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}\)
Detailed Steps for Calculating Probability
Step 1: Identify the Event
Determine the event for which you want to calculate the probability.
Step 2: Determine the Sample Space
List all possible outcomes of the experiment.
Step 3: Calculate the Probability
Use the appropriate rule or formula to calculate the probability of the event.
Examples
Example 1: Rolling a Die
- Scenario: Calculate the probability of rolling a 4 on a fair six-sided die.
- Solution: The sample space is {1, 2, 3, 4, 5, 6}. There is 1 favorable outcome.
- Probability: \(P(4) = \frac{1}{6} \)
Example 2: Drawing a Card
- Scenario: Calculate the probability of drawing an Ace from a standard deck of 52 cards.
- Solution: There are 4 Aces in the deck.
- Probability: \(P(\text{Ace}) = \frac{4}{52} = \frac{1}{13} \).
Example 3: Flipping Coins
- Scenario: Calculate the probability of getting 2 heads in 3 flips of a fair coin.
- Solution: The sample space is {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}. There are 3 favorable outcomes (HHT, HTH, THH).
- Probability: \( P(\text{2 heads}) = \frac{3}{8} \).
Example 4: Conditional Probability
- Scenario: Calculate the probability of drawing a red card given that the card is a face card from a standard deck.
- Solution: There are 6 red face cards (3 hearts and 3 diamonds) out of 12 face cards.
- Probability: \( P(\text{Red | Face}) = \frac{6}{12} = \frac{1}{2} \).
Example 5: Dependent Events
- Scenario: Calculate the probability of drawing 2 kings consecutively without replacement from a standard deck.
- Solution: The probability of drawing the first king is \( \frac{4}{52} \) and the probability of drawing the second king is \( \frac{3}{51} \)
- Probability: \( P(\text{2 Kings}) = \frac{4}{52} \times \frac{3}{51} = \frac{1}{221} \).
Multiple Choice Questions (MCQs)
MCQ 1:
What is the probability of drawing a Queen or a King from a standard deck of 52 cards?
A) \( \frac{1}{13} \)
B) \( \frac{1}{26} \)
C) \( \frac{2}{13} \)
D) \( \frac{4}{52} \)
Answer: c) \( \frac{2}{13} \)
Explanation: There are 4 Queens and 4 Kings in the deck. So, the probability is \( \frac{4+4}{52} = \frac{8}{52} = \frac{2}{13} \).
MCQ 2:
If two events A and B are independent, what is P(A∩B)P(A \cap B)P(A∩B)?
A) \(P(A) + P(B)\)
B) \(P(A) \times P(B|A)\)
C) \(P(A) \times P(B)\)
D) \(\frac{P(A)}{P(B)}\)
Answer: C) \( P(A) \times P(B) \)
Explanation: For independent events, the probability of both events occurring is the product of their individual probabilities.
MCQ 3:
What is the probability of getting at least one head in two flips of a fair coin?
A) \( \frac{1}{4} \)
B) \( \frac{1}{2} \)
C) \( \frac{3}{4} \)
D) \( \frac{1}{8} \)
Answer: C) \( \frac{3}{4} \)
Explanation: The probability of getting at least one head is 1 minus the probability of getting no heads. The probability of no heads \( \frac{1}{4} \). Thus, the probability of at least one head is \( 1 – \frac{1}{4} = \frac{3}{4} \)