Irrational Numbers

Plenty of our tools and products utilize real numbers to denote a numerical value or a numerical measurement. These numerical values or measurements can come in the form of an irrational number. Irrational numbers are a captivating topic in mathematics, fundamental to understanding various concepts in algebra and geometry. This guide provides a thorough exploration of irrational numbers, demystifying their properties and significance. Perfect for teachers and students, it offers clear definitions, practical examples, and an insight into their role in mathematics. With a focus on simplicity and clarity, this guide makes the concept of irrational numbers accessible and intriguing, encouraging a deeper appreciation for the beauty of mathematics.

What are Irrational Numbers – Definition

Irrational Numbers are numbers that cannot be expressed as a simple fraction of two integers. They have non-repeating, non-terminating decimal expansions, making them unique in the number system. This definition is crucial for students to understand as it distinguishes irrational numbers from rational ones and highlights their importance in mathematical concepts and real-world applications.

What is the Best Example of Irrational Numbers?

A classic example of an irrational number is Pi (?). Pi represents the ratio of the circumference of a circle to its diameter and is known for its non-repeating, non-terminating decimal value. Pi is not only fundamental in geometry and trigonometry but also has implications in various scientific and engineering fields. Its properties make it an ideal example to illustrate the concept of irrational numbers and their practical relevance in mathematics.

Irrational Number Symbol

Typically, the symbol “P” is used to denote irrational numbers. This is because irrational numbers are essentially defined as real numbers that are not rational. Hence, the symbol for irrational numbers follows the alphabetical sequence of P, Q, R, representing the progression from the real numbers (R) to rational numbers (Q) and then to irrational numbers (P). More commonly, however, irrational numbers are represented by the set difference of real numbers minus rational numbers, expressed as R – Q or R\Q.

Characteristics of Irrational Numbers

Irrational numbers are a fascinating and integral part of mathematics, characterized by their unique features. They cannot be expressed as a simple fraction, have non-terminating, non-repeating decimal expansions, and are found within the real numbers. Understanding these characteristics is crucial for students to differentiate between rational and irrational numbers and to appreciate the complexity of mathematical concepts.

1. Non-Terminating Decimals: Decimal representation never ends, e.g., Pi (?).
   • Pi (3.14159…) extends infinitely without repetition.
2. Non-Repeating Decimals: No repeating pattern in decimal part, e.g., e (Euler’s Number).
   • Euler’s Number (2.71828…) shows no recurring decimal sequence.
3. Cannot be Expressed as Fractions: No fraction form, e.g., ?2.
   • Square root of 2 can’t be precisely expressed as a fraction.
4. Density in Real Numbers: Exist between any two real numbers, e.g., ?3.
   • There are infinitely many irrational numbers between any two real numbers.
5. Unpredictable Decimal Expansions: Random decimal sequence, e.g., ?5.
   • The square root of 5’s decimals don’t follow a pattern.
6. Inexpressible as Finite or Periodic Continued Fractions: No simple continued fraction representation, e.g., the Golden Ratio (?).
   • Golden Ratio’s continued fraction is infinite.
7. Distribution on the Number Line: Evenly distributed across, e.g., ?7.
   • Irrational numbers like ?7 are found all along the number line.

Properties of Irrational Numbers

Irrational numbers have distinct properties that make them an intriguing subject in mathematics. These properties include their placement on the number line, their algebraic characteristics, and their behavior under various mathematical operations.

1. Closure Property: Not closed under addition, subtraction, or division.
   • Sum or product of two irrational numbers can be rational or irrational.
2. Set Inclusion: Part of the real numbers but not of the rationals.
   • Irrational numbers are included in the set of real numbers (R).
3. Algebraic and Transcendental: Some are algebraic (like ?2), others are transcendental (like ?).
   • Algebraic irrationals satisfy a polynomial equation, while transcendentals do not.
4. Non-Periodicity: Decimal expansions are non-periodic.
   • Unlike rational numbers, their decimal expansion never repeats a pattern.
5. Unpredictable in Nature: Decimals do not exhibit a predictable pattern.
   • Makes them complex and interesting in mathematical calculations.
6. Approximation by Rationals: Can be approximated by rational numbers.
   • Through continued fractions or decimal truncation.
7. Distribution in Intervals: Infinitely many irrational numbers exist in any interval.
   • Between any two numbers, there’s an infinite number of irrationals.

List of Irrational Numbers from 1-100

Listing specific irrational numbers between 1 and 100 involves identifying numbers that cannot be precisely expressed as fractions and have non-repeating, non-terminating decimal expansions. Here are a few notable examples:

1. ?2 (approximately 1.4142): The square root of 2, first known irrational number.
   • Fundamental in geometry, represents the diagonal of a unit square.
2. ?3 (approximately 1.7320): The square root of 3, an irrational number.
   • Appears in equilateral triangles.
3. ? (Pi, approximately 3.14159): Ratio of a circle’s circumference to its diameter.
   • Integral to circular calculations in geometry and trigonometry.
4. e (Euler’s Number, approximately 2.71828): Base of natural logarithms.
   • Crucial in calculus, especially in growth and decay models.
5. ?5 (approximately 2.2360): The square root of 5.
   • Related to the Golden Ratio and appears in the Fibonacci sequence.

Each of these irrational numbers plays a vital role in various mathematical concepts and applications, providing endless opportunities for exploration and discovery.

Irrational Number Theorem and Proof

The Irrational Number Theorem states that numbers that cannot be expressed as a ratio of two integers are irrational. A classic proof involves the square root of 2. Assuming it’s rational and expressible as a simplified fraction a/b leads to a contradiction, as both a and b end up being even, which contradicts the assumption that the fraction is in its simplest form.

1. Proof by Contradiction for ?2: Assumes ?2 is rational, leading to a paradox.
   • Shows that both numerator and denominator must be even, contradicting simplicity.
2. The Golden Ratio (?) is Irrational: Proven using a similar contradiction method.
   • Assumes ? is rational and derives a contradiction.
3. e (Euler’s Number) is Irrational: Proven using a series representation of e.
   • Shows that e cannot be written as a finite or repeating decimal.
4. Pi (?) is Irrational: Proven by Johann Lambert through continued fractions.
   • Demonstrates that no rational number can represent ?.
5. Liouville’s Theorem: Establishes a class of transcendental (and thus irrational) numbers.
   • Proves that certain numbers cannot be roots of any integer polynomial.
6. Hermite’s Proof that e is Irrational: Uses calculus and infinite series.
   • A more complex proof that shows the irrationality of e.
7. Transcendental Numbers are Irrational: Such as Liouville’s constant and e.
   • Transcendental numbers, by definition, are not solutions of any integer polynomial, hence irrational.

How to Find an Irrational Number?

Finding an irrational number involves understanding their properties: non-terminating and non-repeating decimal expansions. Several methods exist, from simple observation to mathematical operations.

1. Square Roots of Non-Perfect Squares: Like ?3, ?5.
   • They cannot be expressed as finite or repeating decimals.
2. Certain Mathematical Constants: Like ? and e.
   • Known to be irrational from mathematical proofs.
3. Cube Roots of Non-Cube Numbers: Such as ³?2, ³?7.
   • Similar to square roots, they don’t resolve to rational numbers.
4. Fractions Involving Pi or e: Like ?/4 or e/3.
   • Any fraction involving an irrational number is irrational.
5. Creating Decimal Expansions: Non-repeating, non-terminating decimals.
   • Constructing a decimal that never repeats or ends.

How to Identify an Irrational Number?

Identifying an irrational number requires understanding its key characteristic: a decimal expansion that neither terminates nor repeats. Here are ways to identify them:

1. Non-repeating Decimals: Infinite decimals without a repeating pattern.
   • Decimals that go on infinitely without repetition.
2. Square Roots of Non-Perfect Squares: Like ?6, ?11.
   • These do not simplify to rational numbers.
3. Numbers Not Solvable by Integer Polynomials: Like ? and e.
   • Transcendental numbers are always irrational.
4. Continued Fraction Representation: Complex and infinite for irrationals.
   • Rational numbers have finite continued fractions.
5. Number Theory Tests: Certain theorems can identify irrational numbers.
   • Applying mathematical theories to determine irrationality.

Set of Irrational Numbers

The set of irrational numbers consists of numbers that cannot be expressed as a simple fraction, where both the numerator and the denominator are integers. These numbers have infinite, non-repeating decimal parts. Understanding irrational numbers is key in advanced mathematics, as they offer a broader perspective of the number system beyond rationals. They are essential in various mathematical fields, including algebra and geometry.

1. ?7 (Square Root of 7): A non-repeating, non-terminating decimal.
   • Cannot be expressed as a fraction, used in geometric calculations.
2. ? – 22/7 (Pi minus Twenty-Two Sevenths): Represents the difference between the approximate and actual value of ?.
   • Illustrates the precision of irrational numbers in calculations.
3. e² (Euler’s Number Squared): An important constant in calculus.
   • Appears in exponential growth models and complex calculations.
4. ?3/2 (Square Root of 3 over 2): Common in trigonometry.
   • Used in calculating angles and distances in triangles.
5. ln 2 (Natural Logarithm of 2): A key logarithmic value.
   • Integral in growth calculations and compound interest formulas.
6. (1+?5)/2 (Golden Ratio): Found in art, nature, and architecture.
   • Represents aesthetic perfection and natural growth patterns.
7. ?2 + ?3 (Square Root of 2 plus Square Root of 3): An algebraic sum of two irrational numbers.
   • Used in advanced geometric proofs and theorems.

Differences Between Rational and Irrational Numbers

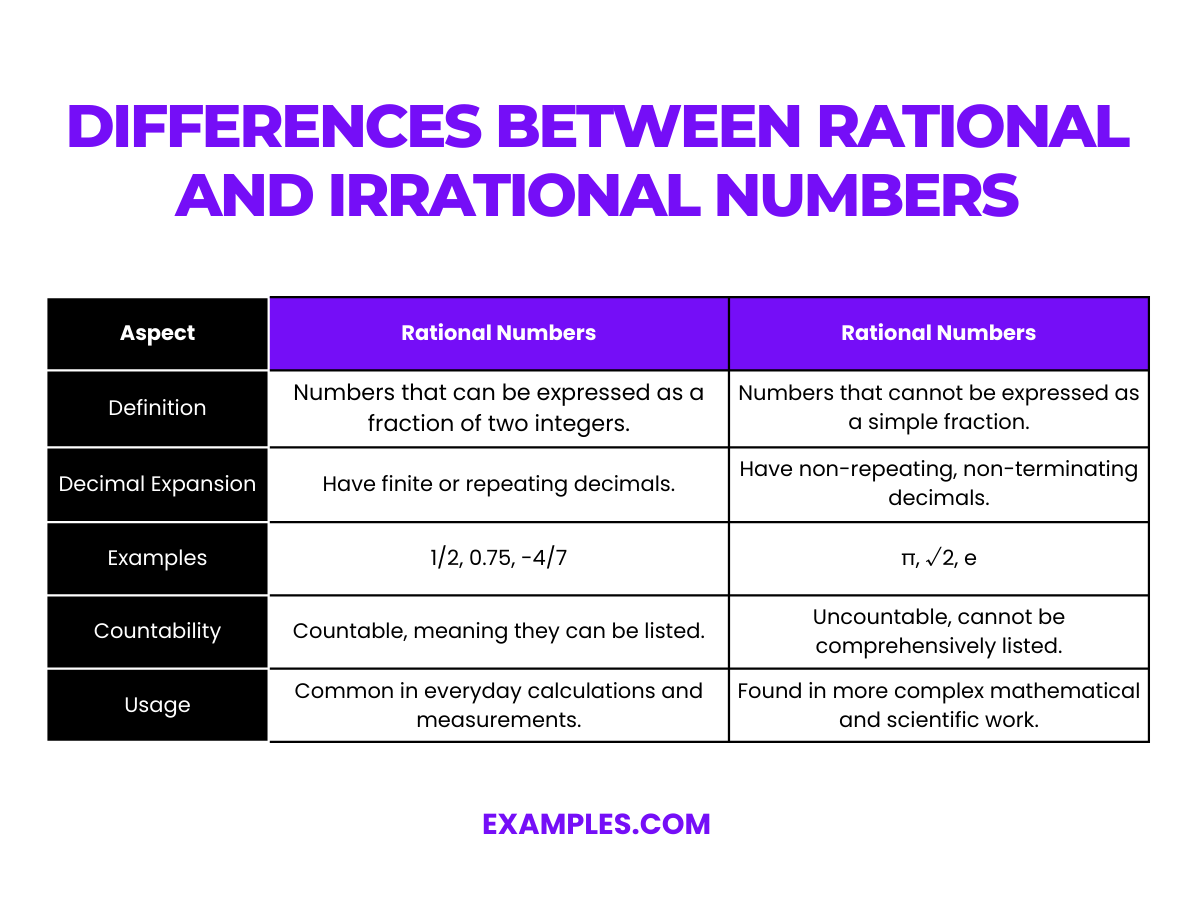
Aspect	Rational Numbers	Rational Numbers
Definition	Numbers that can be expressed as a fraction of two integers.	Numbers that cannot be expressed as a simple fraction.
Decimal Expansion	Have finite or repeating decimals.	Have non-repeating, non-terminating decimals.
Examples	1/2, 0.75, -4/7	?, ?2, e
Countability	Countable, meaning they can be listed.	Uncountable, cannot be comprehensively listed.
Usage	Common in everyday calculations and measurements.	Found in more complex mathematical and scientific work.
Representation	Often represented by the letter ‘Q’.	Frequently symbolized as R – Q or P.
Precision	Exact values can be precisely determined.	Often require approximation for practical use.

Known Irrational Numbers

Well-known irrational numbers include Pi (?), Euler’s Number (e), the Golden Ratio (?), and the square roots of non-square integers like ?2.

Irrational Numbers Square Root

The square roots of non-square integers (e.g., ?2, ?3, ?5) are irrational, characterized by non-repeating, non-terminating decimals.

What is the Set of Irrational Numbers?

The set of irrational numbers consists of all numbers that cannot be expressed as a simple fraction, having infinite, non-repeating decimal expansions.

Simple Irrational Numbers

Simple examples of irrational numbers are ?2, ? – 22/7, and (1+?5)/2 (Golden Ratio), known for their non-repeating, non-terminating decimal nature.

Are Irrational Numbers Real Numbers?

Yes, irrational numbers are real numbers. They are a subset of real numbers that cannot be expressed as a ratio of two integers.

1. Investigating Irrational Numbers

2. Algebra Irrational Numbers

3. Teaching Irrational Numbers Through Trigonometry

How to Prove That a Number is an Irrational Number

A person can categorize a real number as either a rational or an irrational number. To investigate whether a number is irrational, you must dissect the number and compare it to a set of rules.

1.) If the Number is an Equation, Solve the Equation

If the number you want to prove is an equation then you must solve said equation to obtain the unknown number. This is also true for numbers that appear in roots and fractions like ?3 and ?.

2.) Write Down the Number in Standard or Decimal Form

After solving the equation, you will need to write the whole number in its standard and decimal form. This will help you prove that the number is either a rational or an irrational number.

3.) Check if the Number is a Repeating Number/Decimal

After writing down the number in its standard or decimal form, you will need to check if the number is a repeating decimal. This means that if the number’s decimal creates a repeating pattern of numbers, the number is irrational.

4.) Check if the Number is a Non-Terminating Decimal

If the number is Non-repeating, there is still a chance that the decimal is non-terminating. A non-terminating decimal is a number with a decimal that approaches infinity. If the number is a non-terminating decimal, then it is considered an irrational number.

FAQs

Is Pi an irrational number, and why is it important?

Yes, pi (?) is an irrational number as it is a number the people write as a number that reaches an infinite decimal. Ancient Greek mathematicians used the value of pi to calculate the diameter of a circle. A Chinese mathematician had indicated that the ratio of the circumference of the circle is 355/113 or 3.141592. The pi is a concept that a lot of people and professionals use to calculate the circumference of a 3d circular object like a silo or a wheel.

Rational vs. irrational numbers; why are both rational and irrational numbers important in our everyday lives?

Rational numbers and irrational numbers are real numbers that have various rules governing the way they appear. Rational numbers are numbers that people can write in fractions and decimals (Examples of real numbers include 3, ½, and ?4). While irrational numbers are juxtapositions of rational numbers, which appear as numbers that cannot be expressed in fractions and reach an infinite value (Examples of irrational numbers 10/3, ?, and ?2). These real numbers are important because people use rational numbers in everyday measurements and tools, while other tools and objects require the use of irrational numbers to function.

What is a repeating decimal, and how does it relate to irrational numbers?

A repeating decimal is a decimal number that infinitely repeats the same pattern of numbers in its decimal place. An example of a repeating decimal is the quotient of 10/3 (3.333333) which repeats the number 3 an infinite number of times in the decimal place. Irrational numbers are numbers that people cannot express in fractions, decimals, or standard forms without the need to round the number up to a specific decimal place. This means that numbers that are repeating decimals are considered irrational numbers.

Irrational numbers are numbers that people cannot normally write the number in their standard, fraction, and decimal form. People can easily prove if a number is irrational by trying to write the said number in its standard form and contrasting it to a set of criteria that describes irrational numbers.