Preparing for the CFA Exam requires a comprehensive understanding of “Pricing and Valuation of Options,” a fundamental area in financial modeling and risk management. Mastery of option pricing models, such as the Black-Scholes model, binomial trees, and implied volatility measures, is essential. This knowledge provides critical insights into the valuation dynamics of options, enabling analysts to assess factors like time decay, volatility impact, and the Greeks. A strong grasp of Pricing and Valuation of Options empowers candidates to make informed trading and hedging decisions, ultimately supporting the goal of achieving a high CFA score.

Free CFA Practice Test

Learning Objectives

In studying “Pricing and Valuation of Options” for the CFA, you should learn to assess the factors that influence option pricing and the valuation techniques used in financial markets. This includes mastering the Black-Scholes model, understanding binomial tree structures, and applying implied volatility metrics. Develop proficiency in evaluating the Greeks—Delta, Gamma, Theta, Vega, and Rho—to understand the sensitivities of options to market variables. Analyze the effects of underlying asset price movements, time decay, and volatility changes on option values. Evaluate the pricing models’ assumptions and limitations to assess their real-world applicability and effectiveness in risk management. Additionally, gain the ability to apply these skills in practical scenarios, such as constructing option-based hedging strategies, optimizing investment portfolios, and making informed trading decisions based on option valuation techniques.

Key Concepts in Pricing and Valuation of Options

1. Intrinsic Value and Time Value

Intrinsic Value: The value if the option were exercised immediately. For a call option, it’s the difference between the asset’s price and the strike price (if positive); for a put option, it’s the strike price minus the asset’s price.
Time Value: The additional value based on the time remaining until expiration. This component reflects the potential for the option to become profitable as market conditions change.

2. Option Pricing Models

“Option Pricing Models are mathematical frameworks used to determine the fair value of options. These models incorporate various factors—such as the current price of the underlying asset, strike price, time to expiration, volatility, and interest rates—to estimate what an option should cost in the market.”

Binomial Model: A step-by-step approach where the price of an option is modeled across multiple periods. This model is useful for American options, which can be exercised before expiration.
Black-Scholes Model: Used primarily for European options, this continuous model calculates a theoretical option price using factors such as volatility, interest rates, and time to expiration.
Monte Carlo Simulation: Uses random sampling to estimate the price of options, especially useful for complex options that may not fit standard models.

3. The Greeks

Delta: Measures sensitivity to changes in the underlying asset’s price.
Gamma: Indicates the rate of change of delta relative to the underlying asset’s price.
Vega: Sensitivity to volatility changes in the underlying asset.
Theta: Time decay, or the rate at which an option loses value as expiration approaches.
Rho: Sensitivity to interest rate changes.

Types of Options in Pricing and Valuation

Understanding the various types of options is essential for accurate pricing and valuation.

1. Call and Put Options

Call Options: Grant the holder the right to buy the underlying asset at a specified strike price before or at expiration.
Put Options: Allow the holder to sell the underlying asset at a specified strike price before or at expiration.

2. American vs. European Options

American Options: Can be exercised at any time before the expiration date, adding flexibility. This type often requires binomial or lattice models for valuation.
European Options: Can only be exercised on the expiration date, making them simpler to price using models like Black-Scholes.

3. Exotic Options

These are more complex options often customized for specific scenarios. Common exotic options include:
- Asian Options: The payoff depends on the average price of the underlying asset over a certain period.
- Barrier Options: Activated or deactivated once the underlying asset hits a predetermined price level (knock-in or knock-out).
- Binary Options: Provide a fixed payoff if the underlying asset meets certain conditions at expiration.

4. Vanilla Options

Standard call and put options with no additional features, traded on exchanges with fixed expiration dates and strike prices. These are often the primary focus of traditional pricing models like Black-Scholes.

5. Employee Stock Options (ESOs)

Often issued by companies as part of compensation packages, allowing employees to purchase shares at a fixed strike price. These options are typically American-style with vesting periods and restrictions, making their valuation unique.

Key Factors Affecting Option Valuation

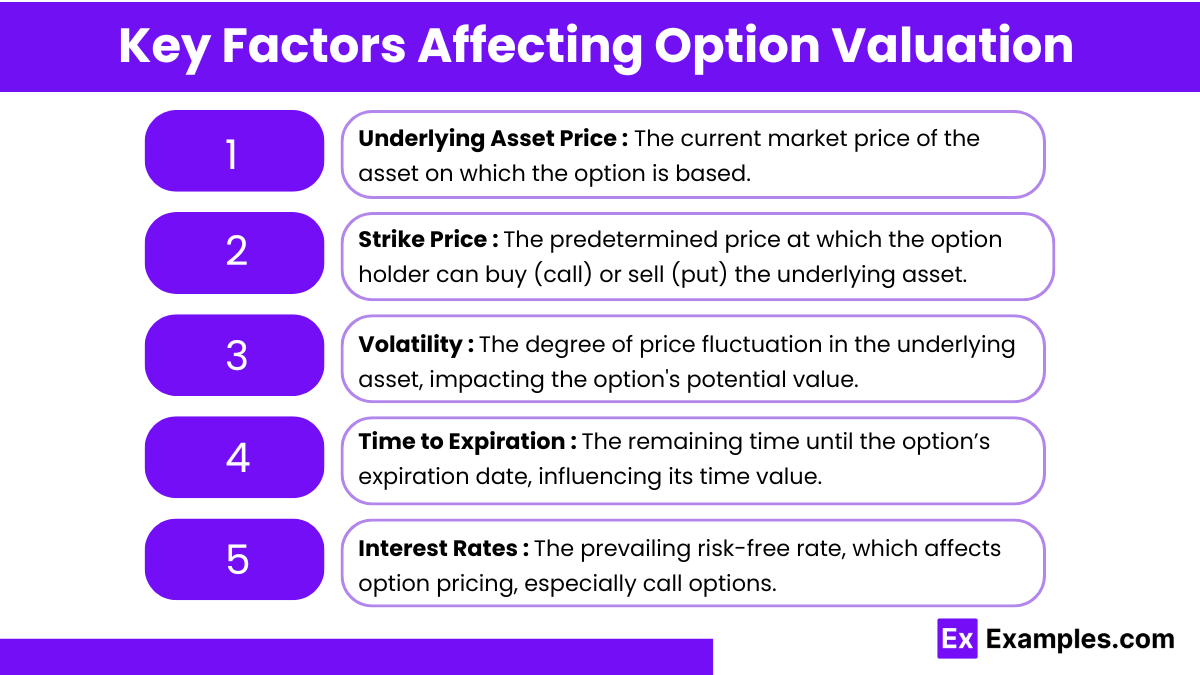
Underlying Asset Price: Directly impacts the intrinsic value of the option. An increase in the asset price generally increases the value of a call option and decreases the value of a put option.
Strike Price: The set price at which the option can be exercised. Options closer to the money (where the strike price is near the current price of the underlying asset) tend to have higher extrinsic values.
Volatility: Higher volatility increases the likelihood that the option will end up in the money, thus raising the option’s premium, especially in terms of time value.
Time to Expiration: The longer the time to expiration, the higher the option’s premium, due to increased potential for favorable price movements. However, as expiration approaches, the time value decays, affecting the option’s overall value.
Interest Rates: Changes in interest rates affect the value of options, especially the cost of carrying the underlying asset. Higher interest rates tend to increase call option values and decrease put option values due to cost-of-carry effects.

Steps to Master Pricing and Valuation of Options

Understand the Basics: Begin with foundational concepts such as types of options, intrinsic vs. extrinsic value, and the time decay of options.
Study the Greeks: Dive deep into the Greeks to understand how changes in market conditions affect option prices. Knowing how to apply the Greeks can aid in risk management and valuation.
Learn Pricing Models: Gain a solid grasp of key pricing models, especially the Black-Scholes and binomial models. Practice applying these models to real-life scenarios and different types of options.
Analyze Market Factors: Explore how external factors like interest rates, volatility, and underlying asset prices impact options. Practice interpreting how these factors influence option values.
Apply Theory to Practice: Use case studies and practical examples to apply theoretical knowledge. Practice constructing hedging strategies, managing option portfolios, and identifying arbitrage opportunities.

Examples

Example 1. Hedging Investment Portfolios

Investors often use options to protect their portfolios from adverse price movements. By accurately pricing and valuing options, they can create effective hedges against potential losses in their holdings. For instance, a portfolio manager holding a significant amount of a stock might purchase put options to guard against a decrease in that stock’s price. Understanding how to price these options ensures that the manager isn’t overpaying for protection and that the hedge aligns with the portfolio’s risk management strategy.

Example 2. Employee Stock Option Plans

Many companies issue stock options as part of employee compensation packages. Properly valuing these options is essential for both the company’s financial statements and employee decision-making. For instance, employees need to understand the intrinsic and time value of their options to decide the best time to exercise them. From a company’s perspective, knowing the option’s fair value helps in accounting for compensation expenses accurately and transparently.

Example 3. Pricing in Volatile Markets

Option pricing models like Black-Scholes or Binomial Models help investors determine fair value in fluctuating markets. In times of high volatility, options become more valuable due to increased uncertainty about the asset’s future price. By using these models, investors can make informed decisions on whether to buy or sell options based on market conditions, enhancing their chances of profitable trades.

Example 4. Speculative Trading on Price Movements

Options offer traders the ability to speculate on the price direction of underlying assets without owning them outright. For instance, a trader who anticipates a rise in a stock’s price might purchase call options to potentially profit from this increase. Understanding pricing helps the trader evaluate whether the premium paid for these options is justified by the expected price movement and the potential for gains.

Example 5. Evaluating Company Mergers and Acquisitions

In corporate finance, options pricing concepts are useful when analyzing potential mergers and acquisitions. For example, in a merger where one company is acquiring another, the acquiring company might offer options as part of the purchase price. Accurately valuing these options ensures that both parties understand the financial implications and that the offer represents a fair exchange of value in the deal structure.

Practice Questions

Question 1

What is the primary factor that affects the value of an option’s time premium?

A) The current price of the underlying asset
B) The time remaining until the option’s expiration
C) The exercise (strike) price of the option
D) The dividend yield of the underlying asset

Correct Answer: B) The time remaining until the option’s expiration

Explanation:
The time premium of an option represents the portion of the option’s price attributed to the remaining time until expiration. As time decreases, this premium also decreases, a phenomenon known as “time decay.” Options with more time until expiration generally have higher time premiums because they hold greater potential for profitable movements in the underlying asset’s price. This potential diminishes as the expiration date approaches, causing the time premium to gradually decrease, ultimately reaching zero at expiration. Therefore, the time remaining until expiration is the primary factor impacting the option’s time premium.

Question 2

Which option pricing model is most commonly used to determine the fair value of European-style options?

A) Black-Scholes model
B) Binomial model
C) Monte Carlo simulation
D) Capital Asset Pricing Model (CAPM)

Correct Answer: A) Black-Scholes model

Explanation:
The Black-Scholes model is the most widely used model for pricing European-style options, which can only be exercised at expiration. It considers factors such as the underlying asset’s current price, strike price, time to expiration, risk-free interest rate, and volatility of the underlying asset. This model provides a closed-form solution to calculate an option’s theoretical price, making it especially useful for European options. The Binomial model (choice B) can also be used for option pricing but is generally applied to American-style options, which allow early exercise. Monte Carlo simulation (choice C) is a more complex model used in cases where option payoffs are path-dependent. The CAPM (choice D) is not used for option pricing; instead, it is used to determine expected returns on assets based on their risk.

Question 3

When would a call option typically be considered “in the money”?

A) When the strike price is equal to the underlying asset’s price
B) When the underlying asset’s price is below the strike price
C) When the underlying asset’s price is above the strike price
D) When the option has a high time premium

Correct Answer: C) When the underlying asset’s price is above the strike price

Explanation:
A call option is considered “in the money” (ITM) when the price of the underlying asset is higher than the option’s strike price. This means the option holder can potentially buy the asset at the lower strike price and sell it at the current higher market price, resulting in a profit. For example, if the strike price of a call option is $50 and the underlying asset is trading at $55, the option is $5 “in the money.” Conversely, if the underlying price is below the strike price, the call option would be “out of the money” (OTM) and would not have intrinsic value. The time premium (choice D) does not determine ITM status; it only adds to the overall premium if there is time left until expiration.