Linear equations in one variable are a fundamental topic in algebra that students must master for success on the Digital SAT exam. These equations involve finding the value of a single variable that makes the equation true. Understanding linear equations in one variable is crucial as it forms the basis for more advanced algebraic concepts and problem-solving skills. Mastery of this topic enables students to solve real-world problems and perform well in standardized tests like the Digital SAT.
Learning Objectives
In studying “Linear Equations in One Variable” for the Digital SAT, you should learn to solve equations that involve a single variable using algebraic manipulation. Understand how to isolate the variable by applying inverse operations, including addition, subtraction, multiplication, and division. Analyze different forms of linear equations, such as those with fractions or parentheses, and practice solving for the unknown variable. Evaluate solutions by substituting them back into the original equation to check for accuracy. Additionally, explore real-world problems that can be modeled and solved using linear equations in one variable.
Linear equations in one variable are equations that can be expressed in the form ax + b = 0, where a and b are constants, and x is the variable. These equations have a unique solution.
General Form

The standard form of a linear equation in one variable is: ax + b = 0
Where:
- a is the coefficient of x
- b is a constant term
- x is the variable
Structure and Components
- Variable: The unknown quantity we need to solve for, represented by x.
- Coefficient: The numerical factor multiplied by the variable, represented by aaa.
- Constant: The fixed value added to or subtracted from the variable term, represented by b.
Solving Linear Equations in One Variable

To solve a linear equation in one variable, follow these steps:
Step 1: Simplify Both Sides
Combine like terms and simplify both sides of the equation if necessary.
For example: 3x + 2 – x = 10
Simplify to: 2x + 2 = 10
Step 2: Isolate the Variable Term
Move all terms containing the variable to one side of the equation and constants to the other side. This often involves adding or subtracting terms on both sides.
For instance: 2x + 2 = 10
Subtract 2 from both sides: 2x = 8
Step 3: Solve for the Variable
Divide both sides by the coefficient of the variable to solve for x.
In this example: x = ![]()
Example Problems
Example 1
Solve the equation: 5x – 7 = 3x + 5
Step-by-Step Solution:
- Subtract 3x from both sides: 5x−3x−7=5
- Add 7 to both sides: 2x=12
- Divide by 2: x=6
Example 2
Solve the equation: 4(2x−1) = 3(x+5)
Step-by-Step Solution:
- Expand both sides: 8x−4 = 3x+15
- Subtract 3x from both sides: 8x−3x−4 = 15
- Add 4 to both sides: 5x = 19
- Divide by 5: x =
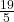
Special Cases

- No Solution: If simplifying the equation results in a contradiction, such as 0 = 5, then the equation has no solution.
Example: 2x+3 = 2x−5
Simplify: 3 = −5 This is a contradiction, so there is no solution. - Infinite Solutions: If simplifying the equation results in a tautology, such as 0 = 0, then the equation has infinitely many solutions.
Example: 3(x−1) = 3x−3
Simplify: 3x−3 = 3x−3 This is always true, so there are infinitely many solutions.
Properties of Linear Equations in One Variable

- Unique Solution: Linear equations in one variable always have a unique solution.
- Graphical Representation: The solution to a linear equation in one variable can be visualized as a point on the number line.
- One Solution: A linear equation in one variable typically has only one solution unless the equation is inconsistent or an identity.
- Degree of the Equation: A linear equation in one variable is of degree 1, meaning the highest power of the variable (x) is 1.
- Transitive Property: If two expressions are equal to a third, they are equal to each other.
Application in Real-World Problems
Linear equations in one variable can be used to solve real-world problems. For instance, finding the cost of items, determining distances, and calculating time.
Example
A company charges a fixed cost of $50 plus $10 per hour for consulting services. If the total bill is $150, how many hours of consulting were provided?
Solution:
Let x be the number of hours of consulting.
50+10x = 150
Subtract 50 from both sides:
10x = 100
Divide by 10:
x=10
So, 10 hours of consulting were provided.
Verifying Solutions
To verify a solution, substitute the value of x back into the original equation and check if both sides are equal.
Example
Verify the solution x=6 for the equation 5x – 7 = 3x + 5.
Substitute x = 6:
5(6) – 7 = 3(6) + 5
30 – 7 = 18 + 5
23 = 23
Both sides are equal, so the solution is verified.
Examples
Example 1
Solve the equation (2x + 7 = 15).
Solution: Subtract 7 from both sides to isolate the term with (x): 2x = 8
Divide both sides by 2: x = 4
The solution is (x = 4).
Example 2
Solve the equation (5x – 9 = 16).
Solution: Add 9 to both sides to move the constant: 5x = 25
Divide both sides by 5: x = 5
The solution is (x = 5).
Example 3
Solve the equation (-3x + 4 = 10).
Solution: Subtract 4 from both sides: -3x = 6
Divide both sides by -3: x = -2
The solution is (x = -2).
Example 4
Solve the equation (7x – 3 = 4x + 12).
Solution: Subtract (4x) from both sides to group like terms: 3x – 3 = 12
Add 3 to both sides: 3x = 15
Divide both sides by 3: x = 5
The solution is (x = 5).
Example 5
Solve the equation ![]() .
.
Solution: Add 5 to both sides: ![]()
Multiply both sides by 3: 2x = 18
Divide both sides by 2: x = 9
The solution is (x = 9).
Practice Questions
Question 1
Solve the equation (4x – 5 = 11).
(A) (x = 2)
(B) (x = 3)
(C) (x = 4)
(D) (x = 5)
Answer: (C) (x = 4)
Explanation:
To solve the equation (4x – 5 = 11), follow these steps:
Step 1: Add 5 to both sides: 4x = 16
Step 2: Divide both sides by 4: x = 4
Thus, the correct answer is (x = 4), which corresponds to option (C).
Question 2
Solve the equation (3x + 2 = 8x – 3).
(A) (x = 1)
(B) (x = -1)
(C) (x = 0)
(D) (x = 2)
Answer: (B) (x = -1)
Explanation:
To solve the equation (3x + 2 = 8x – 3), follow these steps:
Step 1: Subtract (3x) from both sides:2 = 5x – 3
Step 2: Add 3 to both sides: 5 = 5x
Step 3: Divide both sides by 5: x = 1
The correct answer is (x = 1), which corresponds to option (B)
Question 3
Solve the equation: ( 4x – 3 = 2x + 7 ).
(A) ( x = 5 )
(B) ( x = 4 )
(C) ( x = 6 )
(D) ( x = 7 )
Answer: (A) (x = 5)
Explanation:
4x – 3 = 2x + 7
Subtract (2x) from both sides: 2x – 3 = 7
Add 3 to both sides: 2x = 10
Divide by 2: x = 5
We first subtract (2x) from both sides to group like terms, then add 3 to both sides to isolate the (x)-term, and finally divide by 2 to solve for (x). Therefore, (x = 5).


