Percentages

Last Updated: September 25, 2024

Notes

Percentages are a fundamental concept in mathematics that express a number as a fraction of 100. They are widely used in various real-life scenarios, such as calculating discounts, interest rates, and statistical data. A strong understanding of percentages is essential for performing well on the Digital SAT Exam, as questions involving percentages frequently appear in the math section. This topic will cover the basic principles of percentages, how to convert between percentages, decimals, and fractions, and how to solve various types of percentage problems.

Learning Objectives

In this section, you will learn to understand and calculate percentages, convert between percentages, decimals, and fractions, and solve a variety of percentage problems, including percentage increase and decrease, finding the whole from a percentage, and applying percentages to real-world scenarios. By mastering these skills, you will be well-prepared to tackle percentage-related questions on the Digital SAT Exam.

Understanding Percentages

A percentage represents a part of a whole and is expressed as a fraction of 100. For example, 50% means 50 out of 100, or half of the whole. The symbol “%” is used to denote percentages.

Symbol and Notation

The symbol “%” is universally used to denote percentages. When you see this symbol, it indicates that the number preceding it should be divided by 100. For example, 75% is equivalent to $\frac{75}{100}$ or 0.75. This notation simplifies the representation of fractions and makes it easier to communicate proportions and ratios.

Visual Representation

Visual aids can help in understanding percentages better. Imagine a pie chart divided into 100 equal parts. If 50 parts are shaded, it represents 50% of the chart. Similarly, shading 25 parts would represent 25%, and shading the entire chart would represent 100%.

Mathematical Interpretation

Mathematically, a percentage is a way to express a ratio or a fraction where the denominator is 100. It simplifies the process of comparison across different scenarios. For example, saying that 60% of students passed an exam is more intuitive and easier to understand than saying 60 out of 100 students passed.

Examples in Everyday Life

Percentages are used frequently in daily activities. For example, when you see a sale sign that offers 20% off, you know that the price of the item has been reduced by 20% of its original price. If you are a student, your grades might be given in percentages, reflecting the portion of questions you answered correctly on a test. When you read about unemployment rates or population growth in the news, these figures are often expressed as percentages.

Converting Between Percentages, Decimals, and Fractions

To Convert a Percentage to a Decimal: Divide the percentage by 100. For example, 25% becomes 0.25.
To Convert a Decimal to a Percentage: Multiply the decimal by 100. For example, 0.75 becomes 75%.
To Convert a Percentage to a Fraction: Write the percentage as a fraction with a denominator of 100 and simplify if possible. For example, 40% becomes 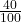$\frac{40}{100}$ which simplifies to $\frac{2}{5}$ .
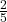To Convert a Fraction to a Percentage:Divide the numerator by the denominator to get a decimal, then multiply by 100. For example, 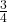$\frac{3}{4}$ becomes 0.75, which is 75%.

Calculating Percentages

Finding the Percentage of a Number: Multiply the number by the percentage (as a decimal). For example, to find 20% of 50, calculate 50×0.20=10.
Finding the Whole from a Percentage: Divide the part by the percentage (as a decimal). For example, if 15 is 30% of a number, calculate $\frac{15}{0.30} = 50$ .
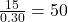Percentage Increase and Decrease:
Increase: Add the percentage increase to the original number. For example, a 20% increase on 50 is 50×1.20=60.
Decrease: Subtract the percentage decrease from the original number. For example, a 20% decrease on 50 is 50×0.80=40.

Solving Percentage Problems

Percentage Change: Calculate the difference between the original and new values, divide by the original value, and multiply by 100. For example, the percentage change from 50 to 70 is $\frac{70 - 50}{50} \times 100 = 40\%$ .
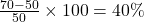Real-World Applications: Percentages are used in various fields such as finance (interest rates, profit margins), retail (discounts, markups), and data analysis (statistical percentages).

Examples of Percentages

Example 1

Finding the Percentage of a Number

Find 25% of 80.

80×0.25=20

So, 25% of 80 is 20.

Example 2:

Converting a Fraction to a Percentage

$\text{Convert } \frac{5}{8} \text{ to a percentage.}$

$\frac{5}{8} = 0.625$

0.625×100=62.5%

$\text{So, } \frac{5}{8} \text{ is 62.5\%.}$

Example 3:

Percentage Increase

A product’s price increases from $40 to $50. What is the percentage increase?

$\text{Percentage Increase} = \frac{50 - 40}{40} \times 100 = 25\%$

So, the percentage increase is 25%.

Example 4:

Percentage Decrease

A population decreases from 2,000 to 1,600. What is the percentage decrease?

$\text{Percentage Decrease} = \frac{2000 - 1600}{2000} \times 100 = 20\%$

So, the percentage decrease is 20%.

Example 5:

Finding the Whole from a Percentage

If 30 is 60% of a number, what is the number?

$\frac{30}{0.60} = 50$

So, the number is 50.

Practice Questions

Question 1

What is 35% of 120?

A) 42
B) 36
C) 45
D) 40

Answer: A

Explanation: To find 35% of 120, multiply 120 by 0.35.
120×0.35=42

Question 2

Convert 0.85 to a percentage.

A) 8.5%
B) 85%
C) 0.085%
D) 850%

Answer: B

Explanation: To convert 0.85 to a percentage, multiply by 100.
0.85×100=85%

Question 3

A car’s value decreases from $20,000 to $16,000. What is the percentage decrease?

A) 15%
B) 20%
C) 25%
D) 30%

Answer: B

Explanation: Calculate the difference and divide by the original value, then multiply by 100.

$\frac{20000 - 16000}{20000} \times 100 = 20\%$