Ratios, Rates, Proportional Relationships, and Units
Understanding ratios, rates, proportional relationships, and units is fundamental for success in many areas of mathematics, including the Digital SAT Exam. These concepts form the basis for comparing quantities, understanding relative sizes, and solving various practical problems. Ratios compare two quantities, rates provide a comparison of different units, proportional relationships describe how two quantities change in relation to each other, and units are standard quantities used in measurement.
Learning Objectives
In this section, you will learn to identify and use ratios, rates, and proportional relationships to solve problems. You will also understand how to work with different units of measurement and convert between them. By mastering these concepts, you will be well-prepared to tackle related questions on the Digital SAT Exam.
Ratios
A ratio is a comparison of two quantities by division. It can be written in three forms: as a fraction, with a colon, or with the word “to.”
- \( \text{Fraction Form}: \frac{a}{b} \)
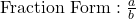
- Colon Form: a:b
- Word Form: a to b
Example: The ratio of 8 apples to 4 oranges can be written as \( \frac{8}{4} \), 8:4, or 8 to 4. Simplified, this is 2:1.
Rates
A rate is a special type of ratio in which the two quantities being compared have different units.
Example: If a car travels 300 miles in 5 hours, the rate is \( \frac{300 \text{ miles}}{5 \text{ hours}} = 60 \text{ miles per hour} \).
Proportional Relationships
A proportional relationship occurs when two quantities always have the same ratio. This can be represented by the equation y=kx, where k is the constant of proportionality.
Example: If a recipe requires 2 cups of flour for every 3 cups of sugar, then the quantities of flour and sugar are in a proportional relationship with a ratio of \(\frac{2}{3}\).
Units
Units are standard quantities used to specify measurements. Common units include meters for length, liters for volume, and grams for weight. It’s often necessary to convert between units to solve problems.
Example: To convert 5 kilometers to meters, use the fact that 1 kilometer = 1000 meters: \( 5 \text{ km} \times 1000 \frac{\text{m}}{\text{km}} = 5000 \text{ m} \).
Working with Units
- Unit Conversion: Use conversion factors to change from one unit to another.
- Dimensional Analysis: A method to convert units by multiplying by fractions that represent the equivalence between units.
Example: Convert 10 inches to centimeters (1 inch = 2.54 cm):
\( 10 \text{ inches} \times 2.54 \frac{\text{cm}}{\text{inch}} = 25.4 \text{ cm} \).
Examples
Example 1: Ratio Simplification
Simplify the ratio 15:25.
Solution:
\( \frac{15}{25} = \frac{3}{5} \)
So, the simplified ratio is 3:5.
Example 2: Rate Calculation
Find the rate if a runner covers 12 kilometers in 1.5 hours.
Solution:
\( \frac{12 \text{ km}}{1.5 \text{ hours}} = 8 \text{ km per hour} \).
Example 3: Proportional Relationship
Determine if the quantities 8 and 12, and 10 and 15, are proportional.
Solution: Calculate the ratios:
\( \frac{8}{12} = \frac{2}{3} \) and \( \frac{10}{15} = \frac{2}{3} \)
Since the ratios are equal, the quantities are proportional.
Example 4: Unit Conversion
Convert 5 gallons to liters (1 gallon = 3.78541 liters).
Solution:
\( 5 \text{ gallons} \times 3.78541 \frac{\text{liters}}{\text{gallon}} = 18.92705 \text{ liters} \)
Example 5: Dimensional Analysis
Convert 60 miles per hour to feet per second (1 mile = 5280 feet, 1 hour = 3600 seconds).
Solution:
\( 60 \text{ miles/hour} \times \frac{5280 \text{ feet}}{1 \text{ mile}} \times \frac{1 \text{ hour}}{3600 \text{ seconds}} = 88 \text{ feet/second} \).
Practice Questions
Question 1
What is the simplified form of the ratio 20:45?
A) 4:9
B) 4:5
C) 9:20
D) 20:45
Answer: A
Explanation: Simplify \(\frac{20}{45}\) by dividing both the numerator and denominator by their greatest common divisor, which is 5:
\( \frac{20 \div 5}{45 \div 5} = \frac{4}{9} \).
Question 2
A cyclist travels 150 miles in 3 hours. What is the cyclist’s rate of speed?
A) 45 miles per hour
B) 50 miles per hour
C) 55 miles per hour
D) 60 miles per hour
Answer: B
Explanation: Calculate the rate by dividing the distance by the time:
\( \frac{150 \text{ miles}}{3 \text{ hours}} = 50 \text{ miles per hour} \).
Question 3
If 3 pounds of apples cost $6, how much would 7 pounds of apples cost, assuming the cost is proportional?
A) $12
B) $14
C) $16
D) $18
Answer: B
Explanation: Set up the proportion \(\frac{3 \text{ pounds}}{6 \text{ dollars}} = \frac{7 \text{ pounds}}{x \text{ dollars}}\). Cross-multiply and solve for x: \( 3x = 42 \), so x=14.