What is the total number of faces on a cube?
4
6
8
12

3D shapes and spatial geometry explore objects with three dimensions: length, width, and depth. This field studies properties, measurements, and relationships of geometric figures like cubes, spheres, and cylinders, extending principles from 2D geometry to the complexities of three-dimensional space.
Three-dimensional shapes, or 3D shapes, are geometric figures that have three dimensions: length, width, and height. Unlike two-dimensional shapes, which exist on a flat plane, 3D shapes occupy space and have volume. Common examples include cubes, spheres, cylinders, cones, and pyramids. Each 3D shape has specific properties such as faces, edges, and vertices. For instance, a cube has six faces, twelve edges, and eight vertices. These shapes are essential in various fields, from architecture and engineering to physics and everyday life, helping to understand and model the physical world around us.
Three-dimensional shapes are characterized by their faces, edges, and vertices. Faces are the flat surfaces of the shape, edges are the lines where two faces meet, and vertices are the points where edges intersect. For example, a cube has 6 faces, 12 edges, and 8 vertices. Understanding these properties helps in identifying and analyzing 3D shapes, crucial in fields like geometry, engineering, and architecture.
The surface area and volume of 3D shapes measure their external and internal space, respectively. Surface area calculates the total area of all faces, while volume measures the space a shape occupies. These properties are essential for practical applications in construction, manufacturing, and various scientific fields.
| Shape | Surface Area | Volume |
|---|---|---|
| Cube | Six times the square of side length | Side length cubed |
| Cuboid | Sum of twice the product of length and width, length and height, and width and height | Product of length, width, and height |
| Sphere | Four times pi times the square of radius | Four-thirds times pi times the cube of radius |
| Cylinder | Sum of two times pi times radius times height and two times pi times the square of radius | Pi times the square of radius times height |
| Cone | Sum of pi times radius times the slant height and pi times the square of radius | One-third times pi times the square of radius times height |
| Pyramid | Sum of base area and one-half the perimeter times slant height | One-third times base area times height |
| Tetrahedron | Square root of three times the square of side length | One-twelfth times the square root of two times the cube of side length |
| Prism | Twice the base area plus the perimeter of base times height | Base area times height |
| Torus | Four times pi squared times the product of major radius and minor radius | Two times pi squared times the square of minor radius times major radius |
Spatial geometry, or three-dimensional geometry, studies geometric figures in three-dimensional space. It involves points, lines, planes, and shapes like cubes, spheres, and pyramids, examining their properties, measurements, and relationships. This field extends principles of 2D geometry to understand and model the physical world in 3D.
Geometry is a branch of mathematics that studies the properties and relationships of points, lines, surfaces, and shapes. It involves understanding and analyzing the size, shape, and dimensions of objects, as well as the spatial relationships between them. Geometry is fundamental in various fields, including art, architecture, engineering, and physics.
The vocabulary of shape and space includes terms like points, lines, angles, surfaces, and solids, describing geometric figures and their properties. It encompasses dimensions, symmetry, congruence, and transformations, essential for understanding spatial relationships and structures.
Spatial relations refer to the ability to understand and interpret the positions, distances, and orientations of objects in space relative to each other. This concept is crucial for navigating environments, understanding maps, and solving geometric problems. It encompasses skills like recognizing shapes, visualizing transformations, and perceiving the spatial organization, vital in fields like architecture, engineering, and everyday activities.
Geometric figures are shapes or forms defined by points, lines, curves, and surfaces. They include two-dimensional shapes like circles, triangles, and squares, as well as three-dimensional shapes like cubes, spheres, and pyramids. These figures are fundamental in studying geometry and understanding spatial relationships and properties.
Physical transformations involve changing the shape, size, or position of objects in space, like rotating, scaling, or translating shapes. Mental transformations refer to visualizing these changes in the mind, crucial for problem-solving and spatial reasoning. Both are essential in fields like geometry, architecture, and cognitive psychology.
3D shapes are geometric figures with three dimensions: length, width, and height.
Spatial geometry studies geometric figures in three-dimensional space, involving points, lines, planes, and shapes.
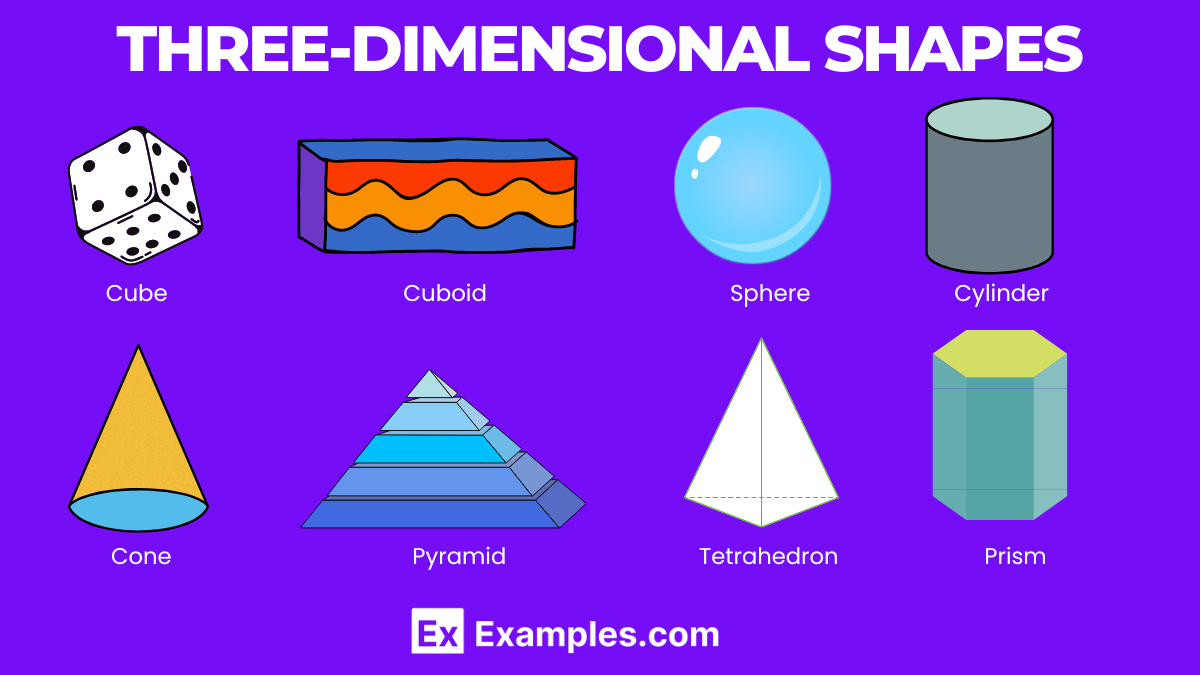
Common 3D shapes include cubes, spheres, cylinders, cones, and pyramids.
A cube has six equal square faces, twelve edges, and eight vertices.
Surface area is the total area of all the faces or surfaces of a 3D shape.
Volume is the measure of the space a 3D shape occupies.
A polyhedron is a 3D shape with flat polygonal faces, straight edges, and sharp vertices.
The five Platonic solids are tetrahedron, cube (hexahedron), octahedron, dodecahedron, and icosahedron.
A prism is a 3D shape with two parallel, congruent bases connected by rectangular faces.
A cylinder is a 3D shape with two parallel circular bases connected by a curved surface.

3D shapes and spatial geometry explore objects with three dimensions: length, width, and depth. This field studies properties, measurements, and relationships of geometric figures like cubes, spheres, and cylinders, extending principles from 2D geometry to the complexities of three-dimensional space.
Three-dimensional shapes, or 3D shapes, are geometric figures that have three dimensions: length, width, and height. Unlike two-dimensional shapes, which exist on a flat plane, 3D shapes occupy space and have volume. Common examples include cubes, spheres, cylinders, cones, and pyramids. Each 3D shape has specific properties such as faces, edges, and vertices. For instance, a cube has six faces, twelve edges, and eight vertices. These shapes are essential in various fields, from architecture and engineering to physics and everyday life, helping to understand and model the physical world around us.
Three-dimensional shapes are characterized by their faces, edges, and vertices. Faces are the flat surfaces of the shape, edges are the lines where two faces meet, and vertices are the points where edges intersect. For example, a cube has 6 faces, 12 edges, and 8 vertices. Understanding these properties helps in identifying and analyzing 3D shapes, crucial in fields like geometry, engineering, and architecture.

Cube
Cuboid (Rectangular Prism)
Sphere
Cylinder
Cone
Pyramid (e.g., Triangular Pyramid, Square Pyramid)
Tetrahedron
Hexahedron
Octahedron
Dodecahedron
Icosahedron
Prism (e.g., Triangular Prism, Pentagonal Prism)
Torus
The surface area and volume of 3D shapes measure their external and internal space, respectively. Surface area calculates the total area of all faces, while volume measures the space a shape occupies. These properties are essential for practical applications in construction, manufacturing, and various scientific fields.
Shape | Surface Area | Volume |
|---|---|---|
Cube | Six times the square of side length | Side length cubed |
Cuboid | Sum of twice the product of length and width, length and height, and width and height | Product of length, width, and height |
Sphere | Four times pi times the square of radius | Four-thirds times pi times the cube of radius |
Cylinder | Sum of two times pi times radius times height and two times pi times the square of radius | Pi times the square of radius times height |
Cone | Sum of pi times radius times the slant height and pi times the square of radius | One-third times pi times the square of radius times height |
Pyramid | Sum of base area and one-half the perimeter times slant height | One-third times base area times height |
Tetrahedron | Square root of three times the square of side length | One-twelfth times the square root of two times the cube of side length |
Prism | Twice the base area plus the perimeter of base times height | Base area times height |
Torus | Four times pi squared times the product of major radius and minor radius | Two times pi squared times the square of minor radius times major radius |
Spatial geometry, or three-dimensional geometry, studies geometric figures in three-dimensional space. It involves points, lines, planes, and shapes like cubes, spheres, and pyramids, examining their properties, measurements, and relationships. This field extends principles of 2D geometry to understand and model the physical world in 3D.
Geometry is a branch of mathematics that studies the properties and relationships of points, lines, surfaces, and shapes. It involves understanding and analyzing the size, shape, and dimensions of objects, as well as the spatial relationships between them. Geometry is fundamental in various fields, including art, architecture, engineering, and physics.
The vocabulary of shape and space includes terms like points, lines, angles, surfaces, and solids, describing geometric figures and their properties. It encompasses dimensions, symmetry, congruence, and transformations, essential for understanding spatial relationships and structures.
Spatial relations refer to the ability to understand and interpret the positions, distances, and orientations of objects in space relative to each other. This concept is crucial for navigating environments, understanding maps, and solving geometric problems. It encompasses skills like recognizing shapes, visualizing transformations, and perceiving the spatial organization, vital in fields like architecture, engineering, and everyday activities.
Geometric figures are shapes or forms defined by points, lines, curves, and surfaces. They include two-dimensional shapes like circles, triangles, and squares, as well as three-dimensional shapes like cubes, spheres, and pyramids. These figures are fundamental in studying geometry and understanding spatial relationships and properties.
Physical transformations involve changing the shape, size, or position of objects in space, like rotating, scaling, or translating shapes. Mental transformations refer to visualizing these changes in the mind, crucial for problem-solving and spatial reasoning. Both are essential in fields like geometry, architecture, and cognitive psychology.
3D shapes are geometric figures with three dimensions: length, width, and height.
Spatial geometry studies geometric figures in three-dimensional space, involving points, lines, planes, and shapes.
Common 3D shapes include cubes, spheres, cylinders, cones, and pyramids.
A cube has six equal square faces, twelve edges, and eight vertices.
Surface area is the total area of all the faces or surfaces of a 3D shape.
Volume is the measure of the space a 3D shape occupies.
A polyhedron is a 3D shape with flat polygonal faces, straight edges, and sharp vertices.
The five Platonic solids are tetrahedron, cube (hexahedron), octahedron, dodecahedron, and icosahedron.
A prism is a 3D shape with two parallel, congruent bases connected by rectangular faces.
A cylinder is a 3D shape with two parallel circular bases connected by a curved surface.
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the total number of faces on a cube?
4
6
8
12
A cylinder has a height of 10 cm and a radius of 4 cm. What is the volume of the cylinder?
320π cm³
400π cm³
480π cm³
640π cm³
How many edges does a rectangular prism have?
8
12
16
20
What is the surface area of a sphere with a radius of 7 cm?
154π cm²
196π cm²
308π cm²
616π cm²
A cone has a height of 12 cm and a radius of 5 cm. What is its surface area?
170π cm²
180π cm²
190π cm²
200π cm²
How many vertices does a triangular prism have?
6
8
10
12
What is the volume of a sphere with a radius of 3 cm?
36π cm³
81π cm³
108π cm³
144π cm³
A pyramid has a square base with a side length of 6 cm and a height of 9 cm. What is the volume of the pyramid?
108 cm³
213 cm³
216 cm³
432 cm³
How many faces does a dodecahedron have?
10
12
14
16
What is the total surface area of a cube with each edge measuring 5 cm?
100 cm²
110 cm²
120 cm²
150 cm²
Before you leave, take our quick quiz to enhance your learning!

