What is the absolute value of -7?
-7
7
0
1

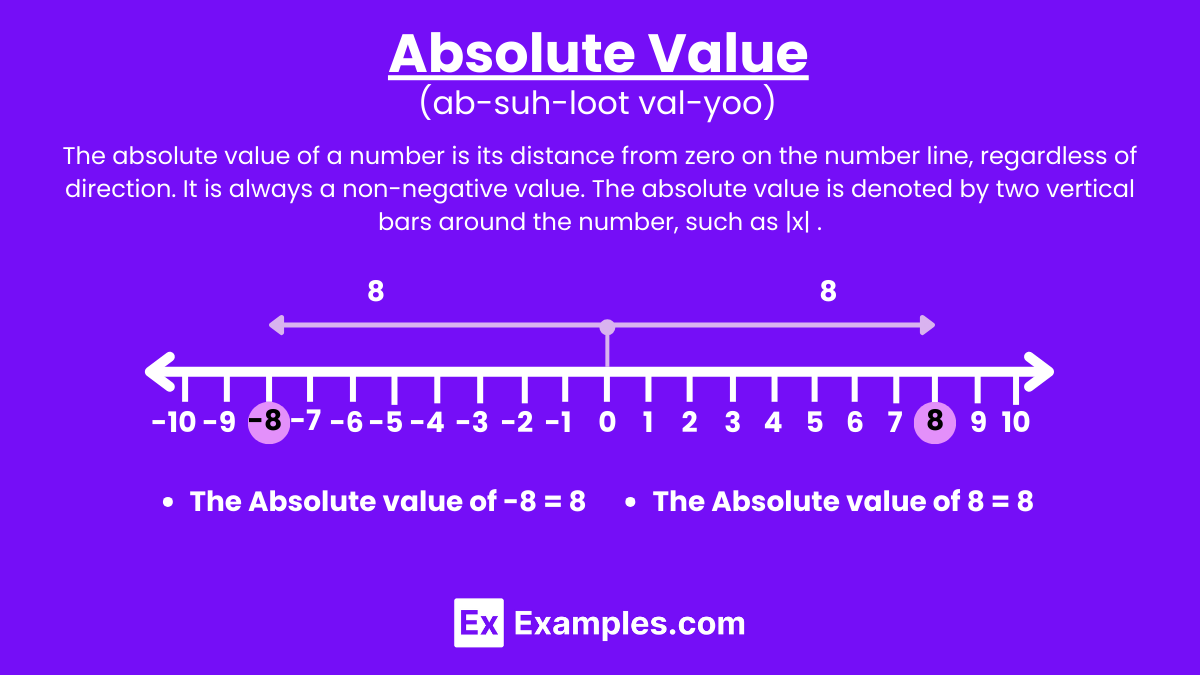
The absolute value of a number is the non-negative value of that number without regard to its sign. It represents the distance of the number from zero on the number line.
The absolute value of a number is its distance from zero on the number line, irrespective of its direction. This means that both positive and negative numbers have the same absolute value. For instance, the absolute value of -5 is 5, and the absolute value of 5 is also 5. Denoted by vertical bars, such as ∣−7∣ = 7 and ∣3∣ = 3, absolute value is always a non-negative number. This concept is crucial in various mathematical contexts, including distance measurement and solving equations.
The absolute value function is a function that returns the absolute value of a number, which is the number’s distance from zero on the number line, regardless of its sign. It is denoted by f(x) = ∣x∣. The function can be defined piecewise as:
This means:
The graph of the absolute value function f(x)=∣x∣ forms a “V” shape, with the vertex at the origin (0,0).
| Property | Mathematical Expression |
|---|---|
| Non-negativity | | x | ≥ 0 |
| Positive-definiteness | | x | = 0 ↔ a = 0 |
| Multiplicativeness | | x × y| = |x| × |y| |
| Subadditivity | | x + y| ≤ | x | + | y | |
| Symmetry | |-x| = |x| |
| Identity of indiscernible (Positive definiteness) | | x – y | = 0 ↔ a = b |
| Triangle inequality (Subadditivity) | | x – y | ≤ | x – z | + | z – x | |
| Preservation of division (Multiplicativeness) | | x / y| = | x | / | y | |
| Equivalent to subadditivity | | x – y | ≥ | | x | – | y | | |
The absolute value (or modulus) of a complex number is a measure of its distance from the origin in the complex plane. Complex numbers are often represented in the form z = a + bi, where a and b are real numbers, and i is the imaginary unit, defined by i² = −1. the absolute value is denoted by ∣z∣ and is defined as: ∣z∣=a²+b² This formula is derived from the Pythagorean theorem and represents the Euclidean distance from the point (a,b) in the complex plane to the origin (0,0).
In the complex plane, a complex number z = a + bi can be represented as a point (a,b). The absolute value ∣z∣ is the length of the line segment connecting the origin to this point. This distance is always non-negative and provides a way to quantify the “size” of a complex number irrespective of its direction.

The absolute value of a real number on a number line represents its distance from zero, regardless of direction. It is always a non-negative value. The absolute value is denoted by vertical bars, such as ∣x∣.
∣x∣ = x if x≥0
∣x∣ = −x if x<0
On the number line, the absolute value of a number represents its distance from zero. Here are a few examples to illustrate this concept:
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the absolute value of -7?
-7
7
0
1
If |x| = 5, what are the possible values of x?
5
-5
5 or -5
0
What is the result of |3 - 8|?
5
- 5
8
-3
Evaluate the expression | -3 + 2 |.
-1
1
-2
3
Solve for x if |x - 4| = 6.
10 or -2
2 or 10
-10 or 2
4 or 6
What is the absolute value of | -12 |?
12
-12
0
24
If |2x - 4| = 8, what are the possible values of x?
6 or -2
4 or -6
0 or 8
2 or -8
Find the absolute value of the result of | -7 - 3 |.
10
-10
8
9
What is the absolute value of | 0 |?
0
1
-1
3
If |x + 2| = 0, what is x?
0
1
2
-2
Before you leave, take our quick quiz to enhance your learning!

