What is the value of x if 3x + 5 = 20?
5
7
10
15


In algebra, operations such as addition, subtraction, multiplication, and division are performed on algebraic expressions, which include numbers, variables, and coefficients. Algebra builds on the foundations of arithmetic by introducing the concept of unknown values, which allows for the formulation and solving of more complex problems
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating these symbols. These symbols represent quantities without fixed values, known as variables. The primary aim of algebra is to solve equations or systems of equations to find the values of these variables.
Algebra is a foundational pillar in the world of mathematics, facilitating the study of numbers, equations, and their relationships through various specialized branches. Each branch focuses on different aspects of algebraic concepts and complexities:
This introductory level lays the groundwork for future studies in algebra. Pre-algebra prepares students by introducing basic mathematical concepts such as arithmetic operations, fractions, decimals, and basic properties of numbers. It’s essential for building a solid foundation for understanding algebraic expressions and equations
This branch delves into more sophisticated structures such as groups, rings, and fields. Abstract algebra explores operations within these structures and their underlying axiomatic systems. It is crucial for advanced mathematical theories and applications in cryptography, physics, and computer science.
Universal algebra studies general algebraic structures rather than specific instances. It deals with properties and theories that apply to all algebraic structures, including groups, rings, fields, and lattices. This branch abstracts the elements common to these structures to gain a deeper understanding of their fundamental aspects.
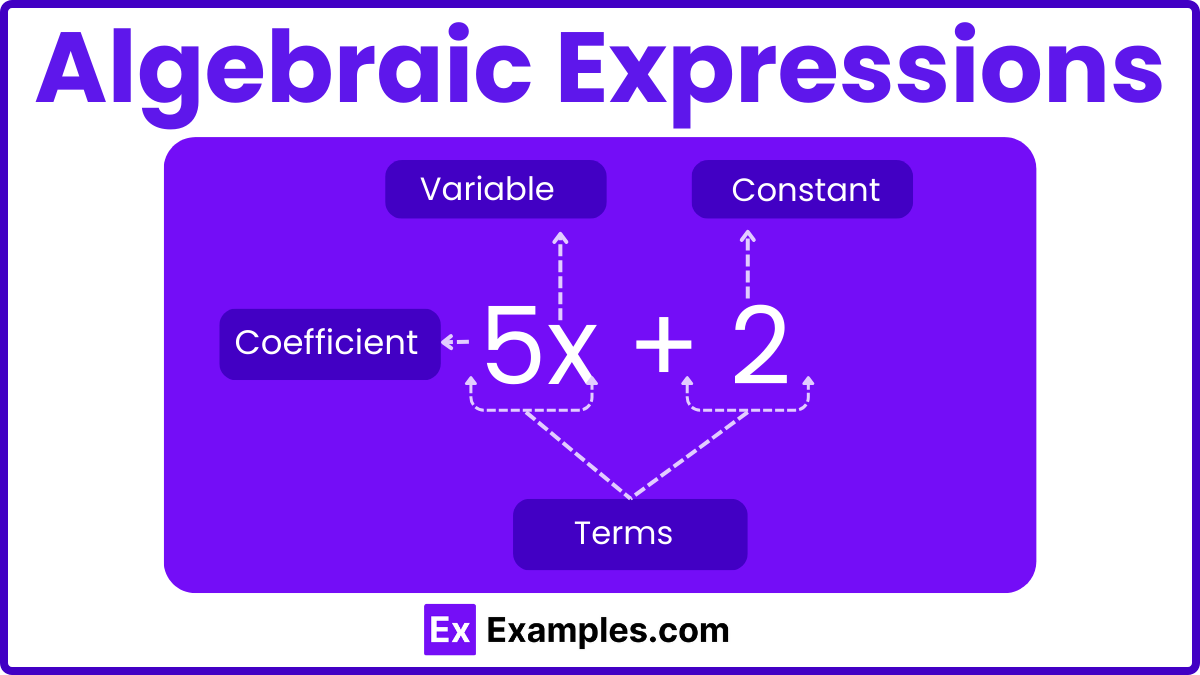
In algebra, an algebraic expression is a mathematical phrase that can include numbers, variables (symbols that represent unknown values), and arithmetic operations—specifically addition (+), subtraction (−), multiplication (×), and division (÷). For instance, the algebraic expression 5x + 6 illustrates how these elements are combined:
Variables in algebraic expressions can be simple, represented by single letters like x, y, or z, or they can be more complex, involving powers (exponents) and products of variables such as 𝑥², 𝑥³, 𝑥ⁿ, 𝑥𝑦, or 𝑥²𝑦.

Algebraic equations can be classified based on the highest degree (the largest exponent) of the variable involved. This classification helps in identifying the nature and complexity of the solutions. Here are the main types:
Linear equations describe relationships between variables, typically x, y, and z, each raised to the first power. These equations are foundational in algebra and are characterized by their simplicity and direct proportionality between variables. A typical linear equation in one variable can be expressed as 𝑎𝑥+𝑏=0, where a and b are constants, and x is the variable. Linear equations are straightforward to solve using basic algebraic operations like addition and subtraction.
Quadratic equations are second-degree equations, meaning the highest power of the variable is two. The standard form of a quadratic equation is 𝑎𝑥²+𝑏𝑥+𝑐=0, where a, b, and c are constants, and 𝑥 represents the variable. These equations are notable for having up to two solutions, which can be real or complex. The solutions, or roots, of a quadratic equation are determined using methods such as factoring, completing the squares, or applying the quadratic formula. Quadratic equations are pivotal in various applications ranging from physics to economics, where they model scenarios involving acceleration and optimization.
Cubic equations involve variables raised to the third power and are expressed in the general form 𝑎𝑥³+𝑏𝑥²+𝑐𝑥+𝑑=0. These equations are more complex than linear and quadratic equations and can have up to three real or complex solutions. Cubic equations are extensively used in fields such as calculus and three-dimensional geometry. They are crucial for solving problems involving cubic curves and volume calculations and often require advanced techniques for solving, including synthetic division and Cardano’s method.
A sequence is an ordered list of numbers where each number is called a term. Sequences can be finite or infinite depending on whether they have a limited or unlimited number of terms. The terms in a sequence are typically defined by a specific rule or formula. For instance, an arithmetic sequence is one where each term after the first is obtained by adding a constant, called the common difference, to the previous term.
Examples of Sequences:
A series is the sum of the terms of a sequence. If the sequence is finite, the series is called a finite series, and the sum can be directly calculated. If the sequence is infinite, the series is called an infinite series, and the sum may or may not converge to a finite value.
Types of Series:
Calculating Series:
Exponents in algebra are used to represent repeated multiplication of the same number, simplifying notation and calculations significantly. Here’s an overview of the basic concepts and rules related to exponents in algebra:
An exponent indicates how many times a base number is multiplied by itself. The expression is written as 𝑎𝑛an, where:
Exponents follow specific rules that make calculations involving powers simpler. Here are the fundamental properties:
Product of Powers Rule: When multiplying two powers that have the same base, add the exponents.
aᵐ×aⁿ=aᵐ⁺ⁿ
Quotient of Powers Rule: When dividing two powers with the same base, subtract the exponents.
aᵐ÷aⁿ=aᵐ⁻ⁿ
Power of a Power Rule: When taking a power of another power, multiply the exponents.
(aᵐ)ⁿ=aᵐˣⁿ
Zero Exponent Rule: Any non-zero base raised to the zero power is equal to one.
a⁰=1
Negative Exponent Rule: A negative exponent indicates division by the base raised to the corresponding positive exponent.
a⁻ⁿ=1/aⁿ
Power of a Product Rule: When raising a product to an exponent, each factor in the product is raised to the exponent.
(ab)ⁿ=aⁿ×bⁿ
Power of a Quotient Rule: When raising a quotient to an exponent, both the numerator and the denominator are raised to the exponent.
(b/a)ⁿ=bⁿ/aⁿ
A logarithm answers the question: “To what exponent must the base b be raised, to produce a certain number y?” Mathematically, this is written as: log𝑏(𝑦)=𝑥logb(y)=x which means 𝑏𝑥=𝑦. In this expression:

Algebraic Formulas are equations that hold true for all values of the variables involved. These Formulas can simplify complex algebraic expressions quickly, making them invaluable in solving mathematical problems.
Square of a Sum: (a+b)²=a²+2ab+b²
Square of a Difference: (a−b)²=a²−2ab+b²
Difference of Squares: (a+b)(a−b)=a²−b²
Square of a Trinomial: (a+b+c)²=a²+b²+c²+2ab+2bc+2ca
Cube of a Sum: (a+b)³=a³+3a²b+3ab²+b³
Cube of a Difference: (a−b)³=a³−3a²b+3ab²−b³
Problem: Calculate the square of 101 using the identity for the square of a sum.
Solution:
We start by recognizing that 101 can be expressed as 100 + 1.
Given: (101)²=(100+1)²
Using the identity for the square of a sum (𝑎+𝑏)²=𝑎²+2𝑎𝑏+𝑏²(a+b)²=a²+2ab+b²
(100+1)²=100²+2×100×1+1²
(101)²=10000+200+1=10201
Algebraic operations are fundamental techniques used to manipulate expressions and solve equations in algebra. Here’s a short and straightforward explanation of the primary operations:
The basic rules or properties of algebra for variables, algebraic expressions, or real numbers a, b and c are as given below,
Commutative Property of Addition: a + b = b + a
Commutative Property of Multiplication: a × b = b × a
Associative Property of Addition: a + (b + c) = (a + b) + c
Associative Property of Multiplication: a × (b × c) = (a × b) × c
Distributive Property: a × (b + c) = (a × b) + (a × c), or, a × (b – c) = (a × b) – (a × c)
Reciprocal: Reciprocal of a = 1/a
Additive Identity Property: a + 0 = 0 + a = a
Multiplicative Identity Property: a × 1 = 1 × a = a
Additive Inverse: a + (-a) = 0
Problem: Solve the equation 2𝑥+3=11 , Find the value of x?
Solution: 2x+3−3=11−3
2x=8
Question 2: Factor and solve the quadratic equation 𝑥²+6𝑥+9=0
Solution:
or more simply,
Answer: 𝑥=−3x=−3.
x=8/2=4
Answer: 𝑥=4
Question 3: Solve the system of equations 2𝑥+3𝑦=6 and 4𝑥−𝑦=5
Solution:
Answer: 𝑥=1.5,𝑦=1y=1.
Question 4: Solve the equation (5𝑥−3)/4=(3𝑥+9)/2
Solution:
Answer: 𝑥=−21x=−21.
Question: Solve for x in the equation 𝑥+5=12
Question: What is the value of 𝑦 when 2𝑦−4=6?
Question: If 3𝑥=9, what is 𝑥?
Question: Calculate 𝑥 if 7𝑥−14=0
Question: What is the coefficient of 𝑥 in the expression 4𝑥+6?
Question: Simplify the expression 5(3𝑥+4).
Question: Find the constant term in the polynomial 6𝑥²+3𝑥+7
Question: If 𝑥−3=10, what is 𝑥?
Question: What is the product of x and 𝑦y if 𝑥=3 and 𝑦=4?
Question: Solve for 𝑦y in the equation 4𝑦+1=9.
Algebra and calculus both have unique challenges. Algebra focuses on solving equations and understanding functions, while calculus deals with concepts of change like derivatives and integrals. Typically, calculus is considered harder as it builds on algebraic principles and introduces more complex ideas.
Algebra can be challenging for many students as it involves abstract thinking and problem-solving skills. It marks a transition from arithmetic to more concept-oriented mathematical studies. How hard it is can depend greatly on the student’s foundation in earlier math concepts.
The four main branches of algebra are: Elementary Algebra, which deals with the basic rules of algebra involving variables and constants; Abstract Algebra, focused on algebraic structures like groups, rings, and fields; Linear Algebra, which involves vector spaces and linear mappings; and Boolean Algebra, which deals with truth values and binary variables.
Among the different types of algebra, Abstract Algebra is often considered the hardest. It dives into advanced topics like groups, rings, and fields, which are more abstract and theoretical compared to the concrete numbers and operations found in elementary algebra.
There are typically three main levels of algebra taught in educational settings: Algebra 1, which covers fundamental algebraic concepts; Algebra 2, which dives deeper into complex equations and functions; and Advanced Algebra, which includes topics such as complex numbers and polynomial division. These levels progressively build depth and complexity
Text prompt
Add Tone
10 Examples of Public speaking
20 Examples of Gas lighting
What is the value of x if 3x + 5 = 20?
5
7
10
15
Solve for y if 2y − 7 = 13.
5
7
10
15
If 4x − 3 = 9, what is x?
2
4
3
6
What is the solution to 5a + 2 = 17?
2
3
4
5
Solve for z in the equation 7z − 4 = 18.
2
4
6
8
What is x if 8x + 6 = 54?
4
5
6
7
Find the value of k if 9k − 3 = 24.
3
4
5
6
If 2x + 4 = 10, what is x?
2
3
4
5
Solve 6y − 8 = 22 for y.
3
4
5
6
What is aaa if 3a + 4 = 19?
4
5
6
7
Before you leave, take our quick quiz to enhance your learning!

