Algebraic Formulas for Class 8, 9, 10, 11, 12

Algebraic Formulas for Class 8, 9, 10, 11, 12

Algebraic formulas are foundational in solving equations and understanding various mathematical concepts across different fields of study.Algebraic formulas are mathematical expressions that describe relationships between variables and constants using algebraic operations such as addition, subtraction, multiplication, division, and exponents. These formulas provide a way to solve problems by substituting numerical values in place of variables to find specific results.

An algebraic identity is an equation that holds true for all values of the variables involved. It guarantees that the left-hand side of the equation is always equivalent to the right-hand side, irrespective of the variable values. These identities are pivotal in solving for unknown variables and simplifying complex algebraic expressions. Below are some commonly used algebraic identities:

Common Algebraic Identities

1. (a + b)² = a² + 2ab + b²

2. (a – b)² = a² – 2ab + b²

3. (a + b)(a – b) = a² – b²

4. (x + a)(x + b) = x² + x(a + b) + ab

Let us look at the algebraic identity: (a + b)² = a² + 2ab + b², and try to understand this identity in algebra and also in geometry. As proof of this formula, let us try to multiply algebraically the expression and try to find the formula. (a + b)² = (a + b) × (a + b) = a(a + b) + b(a + b) = a² + ab + ab + b². This expression can be geometrically understood as the area of the four sub-figures of the below-given square diagram. Further, we can consolidate the proof of the identity (a + b)²= a² + 2ab + b².

Exploring the Identity: (a + b)² = a² + 2ab + b²

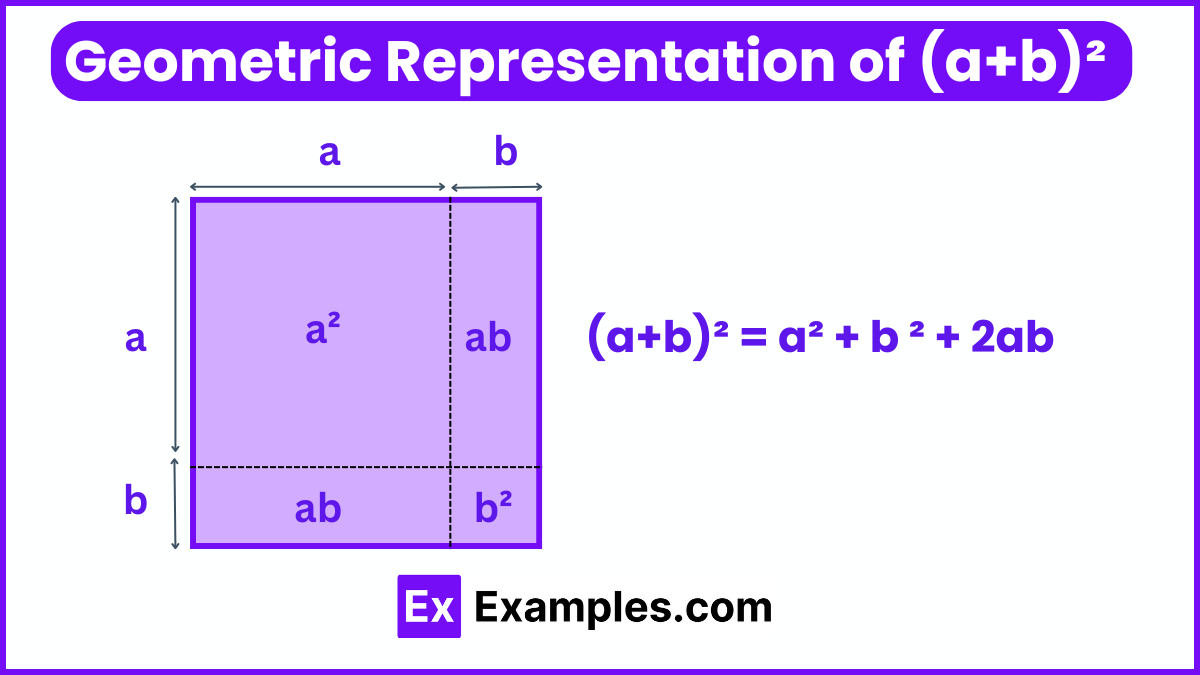
To understand and prove the identity (a + b)² = a² + 2ab + b², let’s perform an algebraic expansion:

(𝑎+𝑏)²=(𝑎+𝑏)×(𝑎+𝑏)=𝑎(𝑎+𝑏)+𝑏(𝑎+𝑏)=𝑎²+𝑎𝑏+𝑎𝑏+𝑏²

This simplifies to:

𝑎²+2𝑎𝑏+𝑏²

What are Algebra Formulas?

An algebraic formula is a concise rule or equation expressed using mathematical and algebraic symbols. It features algebraic expressions on both sides of the equation and is designed to simplify complex algebraic calculations. These formulas are crafted for various mathematical topics, typically involving one or more unknown variables, often denoted as “x.” Common algebraic formulas are versatile and can be applied across multiple mathematical subjects to facilitate quick and accurate problem-solving. This streamlines the process of dealing with intricate problems by providing a standardized method of calculation

Example: (a+b)2 = a2 + 2ab + b2 is an algebraic formula and here,

• (a+b)2 is an algebraic expression

• a2 + 2ab + b2 is a simplified form of an algebraic expression

Algebra Formulas for Class 8

In Class 8, students delve deeper into the world of algebra, exploring equations and formulas that form the cornerstone of advanced mathematical concepts. This stage introduces essential algebraic formulas that enable students to solve a range of problems efficiently. Understanding these formulas is crucial for laying a solid foundation in mathematics as students prepare for more complex topics in higher grades.

(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b
(a + b)(a – b) = a² – b²
(a + b)³ = a3³+ 3a²b + 3ab² + b
(a – b)³ = a³ – 3a²b + 3ab – b²
a + b = (a + b)(a² – ab + b²)
a³ – b³ = (a – b)(a² + ab + b²)
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

Some common laws of exponents, whether involving the same bases with different powers or different bases with the same power, significantly simplify the process of solving complex exponential terms. These rules enable the calculation of higher exponential values without fully expanding the terms. Additionally, understanding and applying these exponential laws is essential for deriving corresponding logarithmic laws, further enhancing their utility in advanced mathematical computations.

• aᵐ. aⁿ = aᵐ⁺ⁿ

• aᵐ/aⁿ = aᵐ⁻ⁿ

• (aᵐ)ⁿ = aᵐⁿ

• (ab)ᵐ = aᵐ. bᵐ

• a⁰= 1

• a⁻ᵐ = 1/aᵐ

Algebra Formulas for Class 9

Logarithms greatly simplify the process of performing complex multiplication and division calculations. For example, the exponential equation 2⁵=32 can be rewritten in logarithmic form as log⁡₂ 32=5. This transformation allows multiplication and division operations between two mathematical expressions to be converted into addition and subtraction when expressed in logarithmic terms. The following properties and formulas of logarithms are instrumental in facilitating these logarithmic calculations.

The important log algebraic formulas that we use most commonly are:

• logₐ (xy) = logₐ x + logₐ y

• logₐ (x/y) = logₐ x – logₐ y

• logₐ xm = m logₐ x

• logₐ a = 1

• logₐ 1 = 0

Algebra Formulas for Class 10

In Class 10, algebra becomes more intricate and sophisticated, focusing on formulas that solve complex equations and deepen understanding of algebraic concepts. Here are some crucial algebra formulas taught in Class 10:

Quadratic Equations

1. Standard Form of a Quadratic Equation
   𝑎𝑥²+𝑏𝑥+𝑐=0
   This is the general form for quadratic equations.

2. Quadratic Formula
   𝑥=−𝑏±√(𝑏²−4𝑎𝑐/2a)
   This formula is used to find the roots of any quadratic equation when factoring is not feasible.

Polynomial Identities

3. Square of a Binomial
   (𝑎±𝑏)²=𝑎²±2𝑎𝑏+𝑏²
   Expands the square of a sum or difference.

4. Cube of a Binomial
   (𝑎±𝑏)³=𝑎³±3𝑎²𝑏+3𝑎𝑏²±𝑏³
   Expands the cube of a sum or difference.

5. Sum and Difference of Cubes
   𝑎³±𝑏³=(𝑎±𝑏)(𝑎²∓𝑎𝑏+𝑏²)
   Useful for factoring the sum or difference of cubes.

Algebraic Techniques

6. Completing the Square
   𝑥²+𝑏𝑥=(𝑥+𝑏²)²−(𝑏/2)²
   A method used to derive the quadratic formula and solve quadratic equations.

Arithmetic and Geometric Progressions

7. Nth Term of an Arithmetic Sequence
   𝑇ₙ=𝑎+(𝑛−1)𝑑
   Where 𝑇𝑛​ is the nth term, 𝑎 is the first term, and 𝑑 is the common difference.

8. Sum of the First n Terms of an Arithmetic Sequence
   𝑆ₙ=𝑛/2[2𝑎+(𝑛−1)𝑑]
   Allows calculation of the sum of the first 𝑛 terms of an arithmetic sequence.

9. Nth Term of a Geometric Sequence
   𝑇ₙ=𝑎𝑟ⁿ⁻¹
   Where r is the common ratio, and 𝑎 is the first term.

10. Sum of the First n Terms of a Geometric Sequence
    𝑆ₙ=𝑎(𝑟ⁿ−1)/(𝑟−1)​ (for 𝑟≠1)
    Useful for finding the sum of terms in a geometric progression.

Algebra Formulas for Class 11

Class 11 algebra introduces more advanced concepts and formulas, further expanding students’ mathematical toolkit. These formulas play a crucial role in solving complex problems and are essential for higher studies in mathematics and related disciplines. Here are some key algebra formulas taught in Class 11:

Polynomial and Rational Functions

1. Polynomial Division (Division Algorithm)
   If 𝑝(𝑥) and 𝑞(𝑥) are polynomials, then there exist polynomials 𝑑(𝑥) and 𝑟(𝑥) such that 𝑝(𝑥)=𝑑(𝑥)⋅𝑞(𝑥)+𝑟(𝑥), where 𝑟(𝑥)=0 or degree of 𝑟(𝑥)< degree of 𝑞(𝑥).

2. Factor Theorem
   If 𝑝(𝑥) is a polynomial, 𝑝(𝑎)=0 implies that (𝑥−𝑎) is a factor of 𝑝(𝑥).

3. Remainder Theorem
   The remainder of the division of 𝑝(𝑥) by (𝑥−𝑎) is 𝑝(𝑎).The remainder of the division of p(x) by (x−a) is p(a).

Complex Numbers

4. Basic Form
   𝑧=𝑎+𝑏𝑖 Where 𝑎 and 𝑏 are real numbers and 𝑖i is the imaginary unit with 𝑖2=−1

5. Conjugate of a Complex Number
   𝑧‾=𝑎−𝑏𝑖

6. Modulus of a Complex Number
   ∣𝑧∣=𝑎²+𝑏²

7. Multiplication and Division of Complex Numbers
   𝑧₁⋅𝑧₂=(𝑎₁𝑎₂−𝑏1𝑏2)+(𝑎1𝑏2+𝑎2𝑏1)𝑖
   𝑧₁/𝑧₂=𝑧₁⋅𝑧₂‾/∣𝑧₂∣²

Sequences and Series

8. Arithmetic Series Sum Formula
   𝑆ₙ=𝑛/2[2𝑎+(𝑛−1)𝑑]

9. Geometric Series Sum Formula
   𝑆𝑛=𝑎 𝑟ⁿ−1/𝑟−1 (for 𝑟≠1)

10. Sum to Infinity of a Geometric Series
    𝑆=𝑎/(1−𝑟)​ (for ∣𝑟∣<1)

Binomial Theorem

11. Binomial Expansion
    (𝑎+𝑏)ⁿ=∑ⁿₖ₌₀=0𝑛(ⁿₖ)𝑎ⁿ⁻ᵏ𝑏ᵏ Where (ⁿₖ) is a binomial coefficient.

Miscellaneous Formulas

12. Permutations and Combinations
    𝑃(𝑛,𝑘)=𝑛!/(𝑛−𝑘)!
    𝐶(𝑛,𝑘)=(ⁿₖ)=𝑛!/𝑘!(𝑛−𝑘)!

Algebra Formulas for Class 12

Class 12 algebra involves advanced concepts that are crucial for both academic and competitive examinations. This level of algebra introduces students to deeper analytical techniques and mathematical theories. Here are some key algebra formulas commonly taught in Class 12:

Functions and Limits

1. Function Composition (𝑓∘𝑔)(𝑥)=𝑓(𝑔(𝑥))
   This formula defines how one function applies to the result of another function.

2. Inverse of a Function 𝑓(𝑓⁻¹(𝑥))=𝑥 ,
   If f and 𝑓−1 are inverse functions.

3. Limit of a Function lim⁡ₓ→ₐ𝑓(𝑥)This is used to find the behavior of a function as 𝑥 approaches a particular value 𝑎.

Derivatives and Integrals

4. Power Rule for Derivatives 𝑑/𝑑𝑥[𝑥ⁿ]=𝑛𝑥ⁿ⁻¹
   This rule is fundamental for finding derivatives of polynomial functions.

5. Product Rule 𝑑/𝑑𝑥[𝑢𝑣]=𝑢′𝑣+𝑢𝑣′
   Where 𝑢 and 𝑣 are functions of 𝑥.

6. Quotient Rule 𝑑/𝑑𝑥[𝑢𝑣]=𝑢′𝑣−𝑢𝑣′𝑣2
   This rule is used for differentiating ratios of functions.

7. Chain Rule 𝑑/𝑑𝑥𝑓(𝑔(𝑥))=𝑓′(𝑔(𝑥))𝑔′(𝑥) Essential for finding the derivative of composite functions.

8. Basic Integration Formulas ∫𝑥ⁿ𝑑𝑥=𝑥ⁿ⁺¹/n+1+𝐶, for 𝑛≠−1

Probability and Statistics

9. Probability of an Event 𝑃(𝐴)=Number of favorable outcomes/Total number of outcomes

10. Binomial Distribution 𝑃(𝑋=𝑘)=(ⁿₖ)𝑝ᵏ(1−𝑝)ⁿ⁻ᵏ Where 𝑛 is the number of trials, 𝑘 is the number of successes, and 𝑝 is the probability of success on a single trial.

Algebra Formulas of Functions

In algebra, functions are fundamental concepts used to describe relationships between variables. They are expressed in the form of equations that map input values to output values. Here’s an overview of key algebraic formulas related to functions that are essential for solving various mathematical problems:

Basic Function Formulas

1. Linear Function
   𝑓(𝑥)=𝑚𝑥+𝑏
   Where 𝑚m is the slope, and 𝑏 is the y-intercept. This formula describes a straight line.
   
   

2. Quadratic Function 𝑓(𝑥)=𝑎𝑥²+𝑏𝑥+𝑐 parabolic curve is characterized by a, 𝑏, and 𝑐 where 𝑎 is not zero.
   
   

3. Polynomial Function 𝑓(𝑥)=𝑎ₙ𝑥ⁿ+𝑎ₙ₋₁𝑥ⁿ⁻¹+…+𝑎₂𝑥²+𝑎₁𝑥+𝑎

Special Functions

4. Absolute Value Function 𝑓(𝑥)=∣𝑥∣ This function returns the absolute value of 𝑥.

5. Exponential Function 𝑓(𝑥)=𝑎𝑥Where 𝑎 is a constant and 𝑎>0 This function is used extensively in growth and decay problems.

6. Logarithmic Function 𝑓(𝑥)=log⁡𝑎(𝑥) Where 𝑎 is the base of the logarithm. This function is the inverse of the exponential function.

Trigonometric Functions

7. Sine Function 𝑓(𝑥)=sin⁡(𝑥)Represents the sine of an angle 𝑥 in radians.

8. Cosine Function 𝑓(𝑥)=cos⁡(𝑥) Represents the cosine of an angle 𝑥.

9. Tangent Function 𝑓(𝑥)=tan⁡(𝑥) Represents the tangent of an angle 𝑥.

Inverse Functions

10. Inverse Function 𝑓⁻¹(𝑦) If 𝑦=𝑓(𝑥), then 𝑥=𝑓⁻¹(𝑦). This formula finds the original input 𝑥 given the function output 𝑦y.

Function Operations

11. Sum of Functions:
    (𝑓+𝑔)(𝑥)=𝑓(𝑥)+𝑔(𝑥)

12. Product of Functions
    (𝑓𝑔)(𝑥)=𝑓(𝑥)𝑔(𝑥)

13. Quotient of Functions
    (𝑓𝑔)(𝑥)=𝑓(𝑥)𝑔(𝑥)

14. Composition of Functions
    (𝑓∘𝑔)(𝑥)=𝑓(𝑔(𝑥))
    This represents the function 𝑓 applied to the result of function 𝑔

Algebra Formulas of Fractions

In algebra, working with fractions involves various operations and manipulations that are foundational for solving equations and simplifying expressions. Here are some essential algebraic formulas for fractions that are useful across a wide range of mathematical problems:

Basic Operations with Fractions

1. Addition and Subtraction of Fractions 𝑎/𝑏+𝑐/𝑑=(𝑎𝑑+𝑏𝑐)/𝑏𝑑
   b/a​+d/c​=ad+bc​/bd
   𝑎/𝑏−𝑐/𝑑=𝑎𝑑−𝑏𝑐/𝑏𝑑
   For adding or subtracting fractions, find a common denominator, typically the product of the two denominators, and adjust the numerators accordingly.

2. Multiplication of Fractions 𝑎𝑏×𝑐𝑑=𝑎𝑐/𝑏c​ Multiplication of fractions is straightforward: multiply the numerators together and the denominators together.

3. Division of Fractions (Multiplication by the Reciprocal)
   𝑎/𝑏÷𝑐/𝑑=𝑎/𝑏×𝑑/𝑐=𝑎𝑑/𝑏𝑐 To divide fractions, multiply by the reciprocal of the divisor.

What are the 4 basic algebra formulas?

The four basic algebra formulas are:
(a + b)²= a² + 2ab + b²
(a – b)² = a² – 2ab – b²
(a + b)(a – b) = a² – b²
(x + a)(x + b) = x² + (a + b)x + ab

What are formulas in algebra?

Algebra formulas are mathematical equations that express relationships between variables. They simplify complex calculations and problem-solving processes. Common formulas include quadratic equations, binomial expansions, and various factorization methods.

How do you solve algebraic Formulae?

To solve algebraic formulas, isolate the variable by performing inverse operations. Simplify the equation step by step, using addition, subtraction, multiplication, division, and factoring techniques. Ensure both sides of the equation remain balanced.

What are the 10 algebraic formulas?

Ten key algebraic formulas are:
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab – b²
(a + b)(a – b) = a² – b²
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
(a – b – c)² = a² + b² + c² – 2ab + 2bc – 2ca
(a + b + c)³ = a³ + b³ + c³ + 3ab(a + b) + 3bc(b + c) + 3ca(c + a)
(a – b – c)³ = a³ – b³ – c³ – 3ab(a – b) + 3bc(b – c) – 3ca(c – a)
a² – b² = (a + b)(a – b)
(a + b + c + d)² = a² + b² + c² + d² + 2ab + 2bc + 2cd + 2da
(a – b)(a² + ab + b²) = a³ – b³

What is the golden rule of algebra?

The golden rule of algebra is to perform the same operation on both sides of an equation to maintain balance. This principle ensures the equation’s equality remains true during the solving process.

What is the hardest algebra formula?

The hardest algebra formula often considered is the Cubic Equation:
ax³+bx²+cx+d=0
Its solution involves complex steps, including the use of the discriminant and Cardano’s formula.

What are the 6 laws of algebra?

The six laws of algebra are:
Commutative Law: a+b=b+a
Associative Law:(a+b)+c=a+(b+c)
Distributive Law:a(b+c)=ab+ac
Identity Law:a+0=a
Inverse Law:a+(−a)=0
Zero Product Law:ab=0 ⟹ a=0 or b=0

How hard is algebra?

Algebra can vary in difficulty depending on the student’s familiarity with mathematical concepts and problem-solving skills. Basic algebra is manageable with practice, while advanced topics may require more effort and understanding.